3 - 拓扑排序
快速入门图论!本文介绍如何求图的出入度,然后介绍图的拓扑排序。
图的度
概念
图节点的度指与该节点相关联的边数,所有节点的度数之和为边数的 2 倍。
在有向图中,节点的度又被分为入度和出度:
- 入度:以节点 V 为终点的有向边的数量。
- 出度:以节点 V 为起点的有向边的数量。
所有点的初度之和与入度之和都是边数。
计算
1557. 可以到达所有点的最少点数目 - 力扣(LeetCode)
这道题看似复杂,实际上只需要统计出所有入度为 0 的点就行。因为从一个入度为 0 的点总能到达有向无环图的各个点。
如何统计入度为零的点呢,只需要把每条有向边的终点从点集中删除即可。参考代码如下:
vector<int> findSmallestSetOfVertices(int n, vector<vector<int>>& edges) { vector<int> ans; unordered_set<int> endSet; for (auto& edge : edges) endSet.insert(edge[1]); for (int i = 0; i < n; ++i) if (!endSet.count(i)) ans.push_back(i); return ans; }
拓扑排序
概念
有向图才有它的拓扑序列,求拓扑序列是图的 BFS 应用。在拓扑序列中,所有的有向边方向都是从前往后的形式。因此,有向无环图 DAG 也是拓扑图,一个 DAG 一定至少存在一个入度为 0 的点。
例如有个有向图:
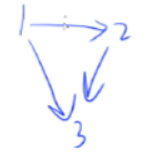
它的出入度统计如下:
| 节点 | 入度 | 出度 |
|---|---|---|
| 1 | 0 | 2 |
| 2 | 1 | 1 |
| 3 | 2 | 0 |
则 1->2->3 就是一个拓扑序列。
思路
用 BFS 来求拓扑序列 / 拓扑排序:
queue <- 所有入度为0的点; while(queue不空) { t <- 队头; 枚举t的所有出边t~j "删掉"t~j(让j的入度d[j]--) if (d[j] == 0) queue <- j; }
最后出队节点的顺序就是要求的拓扑序了,可用 vector 存起来。
练习题
求拓扑序
848. 有向图的拓扑序列 - AcWing 题库
#include <iostream> #include <vector> #include <queue> using namespace std; struct Graph { vector<int> h, d, e, ne; int idx; void add(int a, int b) { e[idx] = b; ne[idx] = h[a]; h[a] = idx++; } Graph(int n, int m) : h(n + 5, -1), d(n + 5), e(m + 5), ne(m + 5), idx(0) {} }; int main() { int n, m; cin >> n >> m; Graph g(n, m); for (int i = 0; i < m; ++i) { int a, b; cin >> a >> b; g.add(a, b); g.d[b]++; } // BFS求拓扑序 vector<int> ans; queue<int> q; for (int i = 1; i <= n; ++i) { if (g.d[i] == 0) q.push(i); } while (!q.empty()) { int cur = q.front(); q.pop(); ans.push_back(cur); for (int idx = g.h[cur]; idx != -1; idx = g.ne[idx]) { int next = g.e[idx]; g.d[next]--; if (g.d[next] == 0) q.push(next); } } if (ans.size() != n) cout << -1 << '\n'; else { for (auto& node : ans) cout << node << " "; cout << '\n'; } }
207. 课程表 - 力扣(LeetCode)
我们把问题抽象一下,就是要求这个图是不是拓扑图,是的话就能学完所有课程。
参考代码如下:
struct Graph { vector<int> h, d, e, ne; int idx; void add(int a, int b) { e[idx] = b; ne[idx] = h[a]; h[a] = idx++; d[b]++; } Graph(int n, int m) : h(n + 5, -1), d(n + 5), e(m + 5), ne(m + 5) {} }; bool canFinish(int numCourses, vector<vector<int>>& prerequisites) { // 先建图 Graph g(numCourses, prerequisites.size()); for (auto& revEdge : prerequisites) { g.add(revEdge[1], revEdge[0]); } // 然后BFS求拓扑序 vector<int> ans; queue<int> q; for (int i = 0; i < numCourses; ++i) { if (g.d[i] == 0) q.push(i); } while (!q.empty()) { int cur = q.front(); q.pop(); ans.push_back(cur); for (int idx = g.h[cur]; idx != -1; idx = g.ne[idx]) { int next = g.e[idx]; g.d[next]--; if (g.d[next] == 0) q.push(next); } } // 看看是不是拓扑图 return ans.size() == numCourses; }
210. 课程表 II - 力扣(LeetCode)
改成求拓扑序列了,修改一下上面的代码就行:
if (ans.size() == numCourses) return ans; else return {};
1462. 课程表 IV - 力扣(LeetCode)
在求拓扑序列的基础上,作进一步要求。得到拓扑序列后,我们应该根据拓扑序列建有向图,使用邻接矩阵存储,然后根据询问一一回答即可。
PS:prerequisites 中边的方向变成从左到右的了。
struct Graph { vector<int> h, d, e, ne; int idx; void add(int a, int b) { e[idx] = b; ne[idx] = h[a]; h[a] = idx++; d[b]++; } Graph(int n, int m) : h(n + 5, -1), d(n + 5), e(m + 5), ne(m + 5) {} }; vector<bool> checkIfPrerequisite(int numCourses, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) { // 建图 Graph g(numCourses, prerequisites.size()); for(auto& edge : prerequisites) { g.add(edge[0], edge[1]); } // BFS求拓扑序 vector<vector<int>> topoGraph(numCourses + 5, vector<int>(numCourses + 5, 0)); queue<int> q; for (int i = 0; i < numCourses; ++i) { if (g.d[i] == 0) q.push(i); } while (!q.empty()) { int cur = q.front(); q.pop(); for (int idx = g.h[cur]; idx != -1; idx = g.ne[idx]) { int next = g.e[idx]; // 建拓扑图, 注意除了直接关系, 还有间接关系 // 因为cur->next可达, 如果i->cur可达, 那么i->next也可达 topoGraph[cur][next] = 1; for (int i = 0; i < numCourses; ++i) topoGraph[i][next] = topoGraph[i][next] | topoGraph[i][cur]; g.d[next]--; if (g.d[next] == 0) { q.push(next); } } } // 回答询问 vector<bool> ans; for (auto& query : queries) { ans.push_back(topoGraph[query[0]][query[1]] == 1); } return ans; }
2115. 从给定原材料中找到所有可以做出的菜 1679 310. 最小高度树 802. 找到最终的安全状态 1962 1203. 项目管理 2419 2603. 收集树中金币 2712 269. 火星词典(会员题) 444. 序列重建(会员题) 1059. 从始点到终点的所有路径(会员题) 1136. 并行课程(会员题)