6 - 下周的光追Part3

发表于 2024-09-02 更新于 2024-09-03 分类于图形学，光追三部曲阅读次数： Waline：本文字数： 16k 阅读时长 ≈ 13 分钟

开始学习大名鼎鼎的光追三部曲系列中的：Ray Tracing: The Next Week！希望我能坚持下去吧。

四边形

接下来我们将往项目中添加四边形图元。

定义四边形

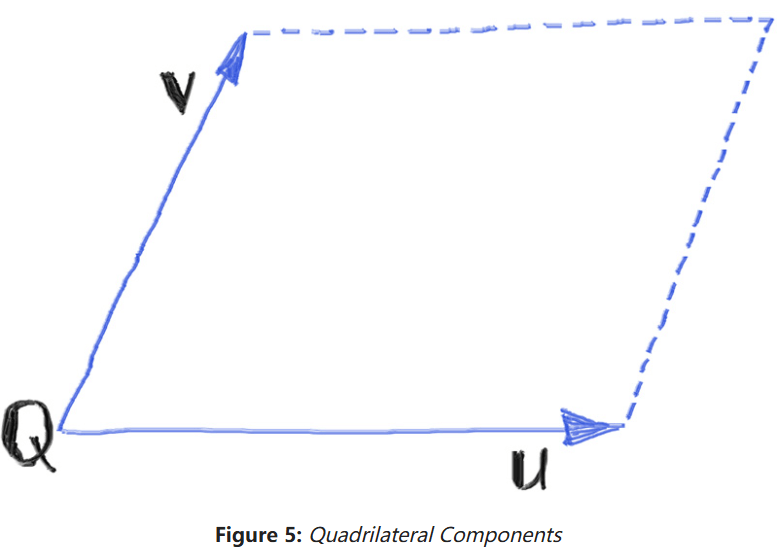
接下来看看四边形的定义，我们将用三个几何量去定义一个四边形：

：四边形的一角。
：代表一侧的向量。可通过得到和相邻的一角。
：代表另一侧的向量。可通过得到和相邻的另一角。

和相对的角可通过得到。这些量都是三维的，尽管四边形自己是一个二维对象。

四边形是平的，因此它AABB的厚度为0（在XY/YZ/ZX平面上）。在光线求交计算时可能会出现数值问题，我们可以通过设置一个极小的厚度来避免这种情况。修改AABB类如下：

class AABB
{
public:
	...
	// 创建一个区间分量为x, y, z的AABB
	AABB(const Interval& x, const Interval& y, const Interval& z)
		: x(x), y(y), z(z)
	{
		pad_to_minimums();
	}
	// 用两个点创建一个AABB
	AABB(const Point3& a, const Point3& b)
	{
		...
		pad_to_minimums();
	}
	// 用三个点创建一个AABB
	AABB(const Point3& a, const Point3& b, const Point3& c)
	{
		...
		pad_to_minimums();
	}
	...

private:
	// 给包围盒设置极小的厚度
	void pad_to_minimums()
	{
		double delta = 0.0001;
		if (x.size() < delta)	x = x.expand(delta);
		if (y.size() < delta)	y = y.expand(delta);
		if (z.size() < delta)	z = z.expand(delta);
	}
};

准备好AABB后，就能编写四边形类Quad了：

class Quad : public Hittable
{
public:
	Quad(const Point3& Q, const Vec3& u, const Vec3& v, shared_ptr<Material> material)
		: Q(Q), u(u), v(v), material(material)
	{
		set_bounding_box();
	}

	// 为四个顶点计算包围盒
	virtual void set_bounding_box()
	{
		AABB bbox_diagonal1 = AABB(Q, Q + u + v);
		AABB bbox_diagonal2 = AABB(Q + u, Q + v);
		bbox = AABB(bbox_diagonal1, bbox_diagonal2);
	}

	bool hit(const Ray& r, Interval ray_t, HitRecord& rec) const override
	{
		// todo
		return false;
	}

private:
	Point3 Q;
	Vec3 u, v;
	shared_ptr<Material> material;
	AABB bbox;
};

光线与四边形求交

光线与四边形求交需要经历三个步骤：

找到包含四边形的平面；
光线和四边形所在平面的求交；
查看交点是否在四边形内部。

我们先看看第二步，光线和平面的求交。类似光线和球面相交，这里给出平面的定义：其中是常量，是平面上任一点。还可将平面的定义写成这样的形式，方便后续计算：给定平面的法向量，从原点到平面上任意点的位置向量，那么可由上面的式子得到，通过点乘：将光线代入，有：求解，得到：这个就是光线和平面的交点，如果光线和平面平行，将为0。对于四边形来说，这可以被立马判定为不相交。而对于其他平面图元，如果小于容忍值，也会判定为不相交。

判断光线和平面求交的方法同样适用于其他平面图元，如三角形，圆盘等。

找到包含四边形的平面

接下来看看第一步，找到包含四边形的平面方程。给定四边形的几何量，想要得到包含四边形的平面方程。

回想一下平面方程的定义，，其中是法向量。为了得到这个法向量，只需通过叉乘即可：刚好在这个平面内，代入上面的点乘式子即可得到：接下来我们将这些值写到Quad类中：

class Quad : public Hittable
{
public:
	Quad(const Point3& Q, const Vec3& u, const Vec3& v, shared_ptr<Material> material)
		: Q(Q), u(u), v(v), material(material)
	{
		Vec3 n = cross(u, v);
		normal = unitVector(n);
		D = dot(normal, Q);

		set_bounding_box();
	}
	...

private:
	Point3 Q;
	Vec3 u, v;
	shared_ptr<Material> material;
	AABB bbox;
	Vec3 normal;
	double D;
};

可以实现针对无限大四边形的hit()函数了：

bool hit(const Ray& r, Interval ray_t, HitRecord& rec) const override
{
	double denom = dot(normal, r.direction());

	// 光线和平面平行, miss
	if (std::fabs(denom) < 1e-8)
	{
		return false;
	}

	// 求解t, 在范围外就返回false
	double t = (D - dot(normal, r.origin())) / denom;
	if (!ray_t.contains(t))
	{
		return false;
	}

	Point3 intersection = r.at(t);

	// 更新rec
	rec.t = t;
	rec.position = intersection;
	rec.material = material;
	rec.set_face_normal(r, normal);

	return true;
}

定位平面上的点

目前，相交点在包含四边形的平面上，但可能在四边形外部或内部。如果在四边形内部，就说明被击中了。为了知道相交点是否在四边形内部，且为了给它分配纹理坐标，我们需要定位平面上的相交点。

我们需要在平面上建系，如图：

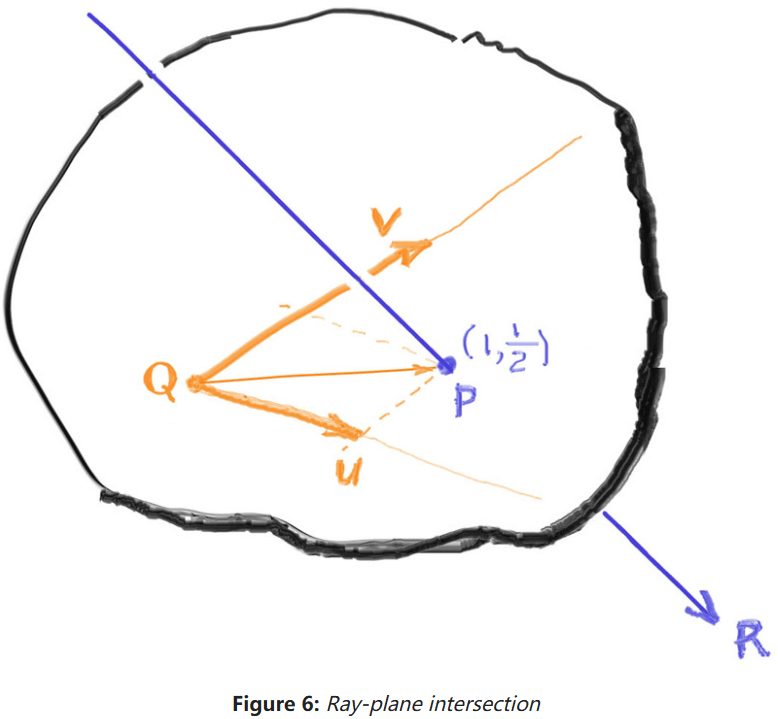
光线和平面相交，留下相交点（不是上面光线定义的P）。经测量，，也就是说在平面坐标系中的坐标为。

一般的，点可以被表示为：而可由下列式子得出（推导详见原教程6.5小节）：其中，是给定四边形的常量，可以先在代码中存储一下：

class Quad : public Hittable
{
public:
	Quad(const Point3& Q, const Vec3& u, const Vec3& v, shared_ptr<Material> material)
		: Q(Q), u(u), v(v), material(material)
	{
		Vec3 n = cross(u, v);
		normal = unitVector(n);
		D = dot(normal, Q);
		w = n / dot(n, n);

		set_bounding_box();
	}
	...
private:
	Point3 Q;
	Vec3 u, v;
	Vec3 w;
	...
};

相交点的UV坐标系内部测试

有了相交点在四边形所在平面的坐标，就能判断其是否在四边形内了。

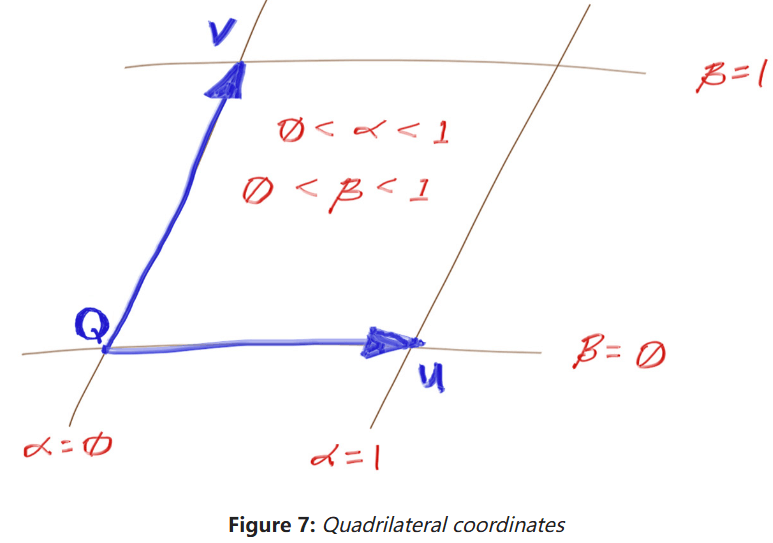
如图，判断相交点是否在四边形内，只需满足如下条件：

继续完善hit()如下：

bool hit(const Ray& r, Interval ray_t, HitRecord& rec) const override
{
	double denom = dot(normal, r.direction());

	// 光线和平面平行, miss
	if (std::fabs(denom) < 1e-8)
	{
		return false;
	}

	// 求解t, 在范围外就返回false
	double t = (D - dot(normal, r.origin())) / denom;
	if (!ray_t.contains(t))
	{
		return false;
	}

	// 相交点是否在四边形内
	Point3 intersection = r.at(t);
	Vec3 planar_hitpt_vector = intersection - Q;
	double alpha = dot(w, cross(planar_hitpt_vector, v));
	double beta = dot(w, cross(u, planar_hitpt_vector));
	if (!is_interior(alpha, beta, rec))
	{
		return false;
	}

	// 更新rec
	rec.t = t;
	rec.position = intersection;
	rec.material = material;
	rec.set_face_normal(r, normal);

	return true;
}

// 判断点是否在四边形内部
virtual bool is_interior(double a, double b, HitRecord& rec) const
{
	Interval unit_interval = Interval(0, 1);
	if (!unit_interval.contains(a) || !unit_interval.contains(b))
	{
		return false;
	}

	rec.u = a;
	rec.v = b;
	return true;
}

接下来新创一个场景看看：

void quadsScene(HittableList& world, Camera& cam)
{
    auto left_red = make_shared<Lambertian>(Color(1.0, 0.2, 0.2));
    auto back_green = make_shared<Lambertian>(Color(0.2, 1.0, 0.2));
    auto right_blue = make_shared<Lambertian>(Color(0.2, 0.2, 1.0));
    auto upper_orange = make_shared<Lambertian>(Color(1.0, 0.5, 0.0));
    auto lower_teal = make_shared<Lambertian>(Color(0.2, 0.8, 0.8));

    world.add(make_shared<Quad>(Point3(-3, -2, 5), Vec3(0, 0, -4), Vec3(0, 4, 0), left_red));
    world.add(make_shared<Quad>(Point3(-2, -2, 0), Vec3(4, 0, 0), Vec3(0, 4, 0), back_green));
    world.add(make_shared<Quad>(Point3(3, -2, 1), Vec3(0, 0, 4), Vec3(0, 4, 0), right_blue));
    world.add(make_shared<Quad>(Point3(-2, 3, 1), Vec3(4, 0, 0), Vec3(0, 0, 4), upper_orange));
    world.add(make_shared<Quad>(Point3(-2, -3, 5), Vec3(4, 0, 0), Vec3(0, 0, -4), lower_teal));

    cam.aspectRadio = 1.0;
    cam.imgWidth = 400;
    cam.samples_per_pixel = 100;
    cam.max_depth = 50;

    cam.vfov = 80;
    cam.lookFrom = Point3(0, 0, 9);
    cam.lookAt = Point3(0, 0, 0);
    cam.vup = Vec3(0, 1, 0);

    cam.defocus_angle = 0;
}

结果如下：

添加其他2D图元

可以举一反三添加其他2D图元了，例如半径为r的圆盘，is_interior()返回true的条件为sqrt(a * a + b * b) < r；例如三角形，条件是a > 0 && b > 0 && a + b < 1。更多图元（圆环等）详见教程仓库src/TheNextWeek/quad.h。

光源

光源是光线追踪的关键部分。早期简单的光追渲染器使用抽象光源，例如点光源，平行光。现代方法则使用更多基于物理的光源，有尺寸和位置属性。为了创建这些光源，我们需要将任一常规物体转化为场景中的光源。

自发光材质

首先让我们创建一个自发光材质DiffuseLight。需要添加一个自发光方程：

class DiffuseLight : public Material
{
public:
	DiffuseLight(shared_ptr<Texture> tex) : tex(tex) {}
	DiffuseLight(const Color& emit) : tex(make_shared<SolidColor>(emit)) {}

	Color emitted(double u, double v, const Point3& p) const override
	{
		return tex->value(u, v, p);
	}

private:
	shared_ptr<Texture> tex;
};

别忘了在父类Material中补充emitted()：

virtual Color emitted(double u, double v, const Point3& p) const
{
	return Color(0, 0, 0);
}

给`ray_color()`添加背景色

接下来，我们想要一个纯黑的背景，以便只有光源在发光。需要修改一下Camera类：

class Camera
{
public:
	double aspectRadio = 1.0;			// 图像的宽高比
	int imgWidth = 100;					// 图像宽度
	int samples_per_pixel = 10;			// 每像素采样数, 即SPP
	int max_depth = 10;					// 光线的最大弹射次数
	Color background;					// 场景的背景色
	...

private:
	...
	Color ray_color(const Ray& r, int depth, const Hittable& world) const
	{
		// 递归退出
		if (depth <= 0)
		{
			return Color(0, 0, 0);
		}

		// 光线没打中物体, 返回背景色
		HitRecord rec;
		if (!world.hit(r, Interval(0.001, infinity), rec))
		{
			return background;
		}

		// 光线打到物体, 看情况返回这条光线的颜色
		Ray scattered;
		Color attenuation;
		Color color_from_emission = rec.material->emitted(rec.u, rec.v, rec.position);

		if (!rec.material->scatter(r, rec, attenuation, scattered))
		{
			return color_from_emission;
		}
		Color color_from_scatter = attenuation * ray_color(scattered, depth - 1, world);

		return color_from_emission + color_from_scatter;
	}
};

别往了给之前的场景设定颜色，因为那些场景没有光源：

cam.background = Color(0.70, 0.80, 1.00);

将物体转换为光源

接下来将一个矩形设置为光源：

void simpleLightScene(HittableList& world, Camera& cam)
{
    auto perlin_tex = make_shared<NoiseTexture>(4);
    world.add(make_shared<Sphere>(Point3(0, -1000, 0), 1000, make_shared<Lambertian>(perlin_tex)));
    world.add(make_shared<Sphere>(Point3(0, 2, 0), 2, make_shared<Lambertian>(perlin_tex)));

    auto diffuse_light = make_shared<DiffuseLight>(Color(4, 4, 4));
    world.add(make_shared<Quad>(Point3(3, 1, -2), Vec3(2, 0, 0), Vec3(0, 2, 0), diffuse_light));

    cam.aspectRadio = 16.0 / 9.0;
    cam.imgWidth = 400;
    cam.samples_per_pixel = 100;
    cam.max_depth = 50;
    cam.background = Color(0, 0, 0);

    cam.vfov = 20;
    cam.lookFrom = Point3(26, 3, 6);
    cam.lookAt = Point3(0, 2, 0);
    cam.vup = Vec3(0, 1, 0);

    cam.defocus_angle = 0;
}

结果如下：

注意到光源比(1, 1, 1)亮，这允许它照亮场景。然后再加一个球体光源试试：

world.add(make_shared<Sphere>(Point3(0, 7, 0), 2, diffuse_light));

结果如下：

创建空的康奈尔盒场景

有了光源和四边形，就能创建经典的康奈尔盒子场景了：

void cornellBoxScene(HittableList& world, Camera& cam)
{
    auto white = make_shared<Lambertian>(Color(0.73, 0.73, 0.73));
    auto red = make_shared<Lambertian>(Color(0.65, 0.05, 0.05));
    auto green = make_shared<Lambertian>(Color(0.12, 0.45, 0.15));
    auto light = make_shared<DiffuseLight>(Color(15, 15, 15));

    world.add(make_shared<Quad>(Point3(555, 0, 0), Vec3(0, 555, 0), Vec3(0, 0, 555), green));
    world.add(make_shared<Quad>(Point3(0, 0, 0), Vec3(0, 555, 0), Vec3(0, 0, 555), red));
    world.add(make_shared<Quad>(Point3(343, 554, 332), Vec3(-130, 0, 0), Vec3(0, 0, -105), light));
    world.add(make_shared<Quad>(Point3(0, 0, 0), Vec3(555, 0, 0), Vec3(0, 0, 555), white));
    world.add(make_shared<Quad>(Point3(555, 555, 555), Vec3(-555, 0, 0), Vec3(0, 0, -555), white));
    world.add(make_shared<Quad>(Point3(0, 0, 555), Vec3(555, 0, 0), Vec3(0, 555, 0), white));

    cam.aspectRadio = 1.0;
    cam.imgWidth = 600;
    cam.samples_per_pixel = 200;
    cam.max_depth = 50;
    cam.background = Color(0, 0, 0);

    cam.vfov = 40;
    cam.lookFrom = Point3(278, 278, -800);
    cam.lookAt = Point3(278, 278, 0);
    cam.vup = Vec3(0, 1, 0);

    cam.defocus_angle = 0;
}

结果如下：

图片噪点非常多是因为光源太小了，所以大多数随机光线都没打到光源再反弹。

场景实例

康奈尔盒场景还有两个方块，它们相对墙面是被旋转过的。首先，先实现一个创建盒子的函数，通过创建包含6个矩形的HittableList：

// Quad.hpp
// 返回由两个点确定的3D盒子
inline shared_ptr<HittableList> box(const Point3& a, const Point3& b, shared_ptr<Material> material)
{
	auto sides = make_shared<HittableList>();

	Point3 min = Point3(std::fmin(a.x(), b.x()), std::fmin(a.y(), b.y()), std::fmin(a.z(), b.z()));
	Point3 max = Point3(std::fmax(a.x(), b.x()), std::fmax(a.y(), b.y()), std::fmax(a.z(), b.z()));
	Vec3 dx = Vec3(max.x() - min.x(), 0, 0);
	Vec3 dy = Vec3(0, max.y() - min.y(), 0);
	Vec3 dz = Vec3(0, 0, max.z() - min.z());
	sides->add(make_shared<Quad>(Point3(min.x(), min.y(), max.z()), dx, dy, material));	// 前
	sides->add(make_shared<Quad>(Point3(max.x(), min.y(), max.z()), -dz, dy, material));	// 右
	sides->add(make_shared<Quad>(Point3(max.x(), min.y(), min.z()), -dx, dy, material));	// 后
	sides->add(make_shared<Quad>(Point3(min.x(), min.y(), min.z()), dz, dy, material));	// 左
	sides->add(make_shared<Quad>(Point3(min.x(), max.y(), max.z()), dx, -dz, material));	// 上
	sides->add(make_shared<Quad>(Point3(min.x(), min.y(), min.z()), dx, dz, material));	// 下

	return sides;
}

然后在场景中添加盒子：

world.add(box(Point3(130, 0, 65), Point3(295, 165, 230), white));
world.add(box(Point3(265, 0, 295), Point3(430, 330, 460), white));

结果如下：

有了盒子后，接下来要将它们旋转。在光线追踪中，这通常由实例完成。实例是场景中几何图元的拷贝，同图元的每个实例都是独立的，这意味着对一个实例进行平移和旋转不会影响其他实例。

实例的平移

在光线追踪中，平移物体不如平移光线。例如下图将粉盒子向右平移得到黑盒子：

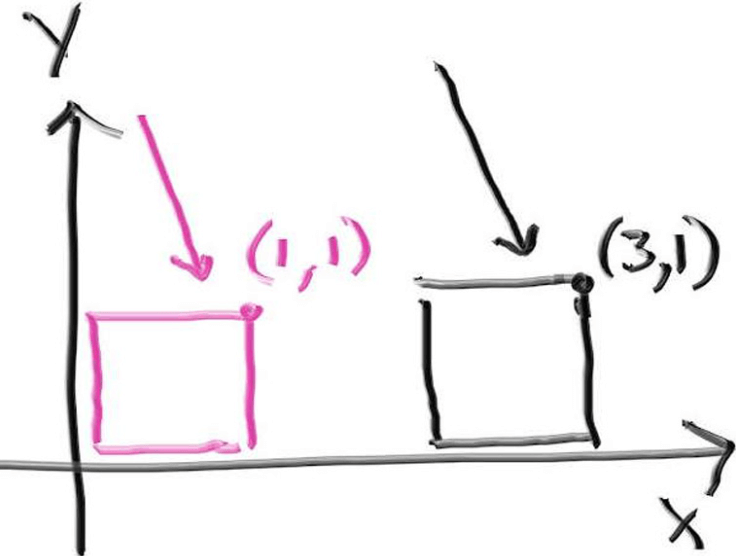
与其让盒子向右移动，不如让光线向左移动，这样盒子就“相对向右移动”了，和摄像机实现移动的原理一样。但还需要注意的是，相交点是和盒子一起移动的，因此如果向左移动后的光线仍打到盒子，就让相交点向右移动。

实现平移的类Translate如下：

class Translate : public Hittable
{
public:
	Translate(shared_ptr<Hittable> object, const Vec3& offset)
		: object(object), offset(offset)
	{
		bbox = object->bounding_box() + offset;
	}

	bool hit(const Ray& r, Interval ray_t, HitRecord& rec) const override
	{
		// 让光反向移动, 以实现物体移动的效果
		Ray offset_r(r.origin() - offset, r.direction(), r.time());

		// 移动后的光是否打到物体, 是的话就让相交点正向移动
		if (!object->hit(offset_r, ray_t, rec))
		{
			return false;
		}
		rec.position += offset;
		return true;
	}

	AABB bounding_box() const override { return bbox; }

private:
	shared_ptr<Hittable> object;
	Vec3 offset;
	AABB bbox;
};

别忘了重载AABB类和Interval类的运算符：

// aabb.hpp
...
const AABB AABB::empty = AABB(Interval::empty, Interval::empty, Interval::empty);
const AABB AABB::universe = AABB(Interval::universe, Interval::universe, Interval::universe);

inline AABB operator+(const AABB& bbox, const Vec3& offset)
{
	return AABB(bbox.x + offset.x(), bbox.y + offset.y(), bbox.z + offset.z());
}

inline AABB operator+(const Vec3& offset, const AABB& bbox)
{
	return bbox + offset;
}

// interval.hpp
...
const Interval Interval::empty = Interval(+infinity, -infinity);
const Interval Interval::universe = Interval(-infinity, +infinity);

inline Interval operator+(const Interval& ival, double displacement)
{
	return Interval(ival.min + displacement, ival.max + displacement);
}

inline Interval operator+(double displacement, const Interval& ival)
{
	return ival + displacement;
}

实例的旋转

直接给出绕轴逆时针旋转的公式：

绕X轴逆时针旋转：绕Y轴逆时针旋转：绕Z轴逆时针旋转：在之前的平移中，我们按照如下想法实现了平移实例类：

将光线逆向移动offset；
移动后的光线是否和物体相交；
是的话就将相交点正向移动offset。

这种想法实际上就是改变坐标系：

将光线从世界坐标系转换到物体的模型坐标系；
在模型坐标系中，光线是否和物体相交；
是的话就将相交点从模型坐标系转换到世界坐标系。

也可以按这种思想去研究旋转这一情况。此外，旋转一个物体还将改变它表面的法线，也能通过上述公式去旋转法线。（但是缩放不是这样子的，如果要实现缩放还需研究表面法线变换。）

实现旋转的类Rotate如下：

enum class RotateAxis { X, Y, Z };

class Rotate : public Hittable
{
public:
	Rotate(shared_ptr<Hittable> object, RotateAxis axis, double angle)
	: object(object), axis(axis), angle(angle)
	{
		bbox = object->bounding_box();

		// 利用线性插值找旋转后的bbox
		Point3 min(infinity, infinity, infinity);
		Point3 max(-infinity, -infinity, -infinity);

		for (int i = 0; i < 2; ++i)
		{
			for (int j = 0; j < 2; ++j)
			{
				for (int k = 0; k < 2; ++k)
				{
					double x = i * bbox.x.max + (1 - i) * bbox.x.min;
					double y = j * bbox.y.max + (1 - j) * bbox.y.min;
					double z = k * bbox.z.max + (1 - k) * bbox.z.min;

					Vec3 tester = rotate(Vec3(x, y, z), axis);
					for (int c = 0; c < 3; ++c)
					{
						min[c] = std::fmin(min[c], tester[c]);
						max[c] = std::fmax(max[c], tester[c]);
					}
				}
			}
		}

		bbox = AABB(min, max);
	}

	bool hit(const Ray& r, Interval ray_t, HitRecord& rec) const override
	{
		// 首先逆向旋转光线, 将光线从世界坐标系转换为模型坐标系
		Point3 origin = rotate(r.origin(), axis, false);
		Vec3 direction = rotate(r.direction(), axis, false);
		Ray rotated_r(origin, direction, r.time());

		// 在模型坐标系中, 光线是否和物体相交
		if (!object->hit(rotated_r, ray_t, rec))
		{
			return false;
		}

		// 是的话就将正向旋转相交点和法线, 从模型坐标系转换到世界坐标系
		rec.position = rotate(rec.position, axis);
		rec.normal = rotate(rec.normal, axis);

		return true;
	}

	AABB bounding_box() const override { return bbox; }

private:
	shared_ptr<Hittable> object;
	RotateAxis axis;
	double angle;
	AABB bbox;

	// 默认按逆时针旋转向量Vec
	Vec3 rotate(const Vec3& vec, RotateAxis axis, bool is_ccw = true) const
	{
		double radians = degrees_to_radians(angle);
		if (!is_ccw)
		{
			radians = -radians;
		}
		double sin_theta = std::sin(radians);
		double cos_theta = std::cos(radians);

		Vec3 ret;
		if (axis == RotateAxis::X)
		{
			ret.e[0] = vec.x();
			ret.e[1] = (cos_theta * vec.y()) - (sin_theta * vec.z());
			ret.e[2] = (sin_theta * vec.y()) + (cos_theta * vec.z());
		}
		else if (axis == RotateAxis::Y)
		{
			ret.e[0] = (cos_theta * vec.x()) + (sin_theta * vec.z());
			ret.e[1] = vec.y();
			ret.e[2] = (-sin_theta * vec.x()) + (cos_theta * vec.z());
		}
		else if (axis == RotateAxis::Z)
		{
			ret.e[0] = (cos_theta * vec.x()) - (sin_theta * vec.y());
			ret.e[1] = (sin_theta * vec.x()) + (cos_theta * vec.y());
			ret.e[2] = vec.z();
		}

		return ret;
	}
};

然后调整下两个盒子：

shared_ptr<Hittable> box1 = box(Point3(0, 0, 0), Point3(165, 330, 165), white);
box1 = make_shared<Rotate>(box1, RotateAxis::Y, 15);
box1 = make_shared<Translate>(box1, Vec3(265, 0, 295));
world.add(box1);
shared_ptr<Hittable> box2 = box(Point3(0, 0, 0), Point3(165, 165, 165), white);
box2 = make_shared<Rotate>(box2, RotateAxis::Y, -18);
box2 = make_shared<Translate>(box2, Vec3(130, 0, 65));
world.add(box2);

最终结果如下：

参考资料

Ray Tracing: The Next Week

四边形

定义四边形

光线与四边形求交

找到包含四边形的平面

定位平面上的点

相交点的UV坐标系内部测试

添加其他2D图元

光源

自发光材质

给ray_color()添加背景色

将物体转换为光源

创建空的康奈尔盒场景

场景实例

实例的平移

实例的旋转

参考资料

给`ray_color()`添加背景色