4 - 算法
本文将深入介绍标准库中算法库相关内容。标准库中包含了大量泛型算法,这些算法大部分都可以应用于任何容器的元素,通过这些算法,可在容器中查找、排序和处理元素,并执行其他大量操作。算法不仅 独立于底层元素的类型,而且 独立于操作的容器的类型,算法仅使用迭代器接口执行操作,而不去操作容器本身。
有关算法库的知识可以去微软开发者文档里找。
算法概述
前面说到,算法仅使用迭代器接口执行操作。并且,算法对传递给它们的迭代器有一些要求。例如,copy_backward()需要双向迭代器,用于从最后一个元素开始,将元素从一个序列拷贝到另一个序列;stable_sort()需要随机访问迭代器,用于在原地对元素进行排序的同时保持重复元素的顺序。而forward_list容器只有前向迭代器,因此不能使用这些算法。
大部分算法都定义在<algorithm>中,一些数值算法在<numeric>中。从C++20开始,大多数算法都是constexpr,这意味着它们可以用于constexpr函数的实现。
接下来以find(),find_if()和accumulate()算法为例,介绍一下算法该怎么用:
find()和find_if()
find()可在某个迭代器范围内查找特定元素,这个算法返回目标元素的迭代器,如果找不到就返回参数中的尾迭代器:
vector<int> iVec{ 1, 2, 3, 5 };
// C++17的if初始化语法
if (auto iter{ find(cbegin(iVec), cend(iVec), 3) }; iter != cend(iVec))
{
// 输出Find element 3
cout << "Find element " << *iter << endl;
}一些容器(map, set等)以成员方法的形式提供自己的.find()版本,应该使用它们提供的版本,因为针对特定数据结构做过优化。例如在map中用std::find()是线性时间,用map.find()则是对数时间。
find_if()额外接收一个可调用对象作为参数,其应返回true或false。例如要找到一个≥4的元素:
vector<int> iVec{ 1, 2, 3, 5 };
auto iter{ find_if(cbegin(iVec), cend(iVec), [](int elem)
{
return elem >= 4;
}) };
if (iter != cend(iVec))
{
// 输出5
cout << *iter;
}accumulate()
accumulate()算法可以计算指定范围内的元素总和,在<numeric>中定义。它接收一组迭代器的范围,一个计算的初始值,以及一个可选的可调用对象:
vector<int> iVec{ 1, 2, 3, 5 };
int res{ accumulate(cbegin(iVec), cend(iVec), 0) };
cout << res; // 11上例计算该vec内所有元素的总和,也能通过编写lambda表达式,将其改成计算所有元素的乘积:
int res{ accumulate(cbegin(iVec), cend(iVec), 1, [](int v1, int v2)
{
return v1 * v2;
})}; // 30在算法中使用移动语义
和容器一样,算法库也做了相关优化,以便在合适的时候使用移动语义,而不是去进行昂贵的拷贝操作。因此,如果我们自定义的类要存放到容器里,就得实现移动语义(实现移动构造函数和移动赋值运算符,并标记为noexcept)。
算法回调
有时候可能需要在回调函数里进行一些记录,例如这里想记录find_if()算法内回调函数调用了几次:
vector<int> iVec{ 1, 2, 3, 5 };
auto overThree{ [cnt = 0](int elem) mutable
{
cout << ++cnt << endl;
return elem >= 3;
} };
find_if(cbegin(iVec), cend(iVec), overThree);
find_if(cbegin(iVec), cend(iVec), overThree);却输出如下图的结果:
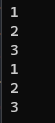
这是因为find_if()中接收的可调用对象是 overThree的 拷贝,为了避免回调被算法复制,可以使用std::ref()函数向算法传递overThree的 引用:
find_if(cbegin(iVec), cend(iVec), ref(overThree));
find_if(cbegin(iVec), cend(iVec), ref(overThree));这样输出结果就对了:
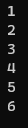
算法详解
这里列举一些常见的算法,并将它们分类展示。
非修改序列算法
非修改序列算法是不修改它们所操作的元素序列的算法。
搜索算法
前面介绍了find()和find_if(),其实还有其他变种:
| 算法 | 解释 |
|---|---|
find_if_not() | 返回指示的范围中不满足条件的第一个元素。 |
adjacent_find() | 搜索相等或满足指定条件的两个相邻元素。 |
find_first_of() | 找到指定范围内首次出现的子序列内任意1值;可接受一个二元谓词 |
search()* | 找到指定范围内首次出现的子序列;可接受一个二元谓词 |
find_end() | 找到指定范围内最后一次出现的子序列;可接受一个二元谓词 |
search_n() | 找到指定范围内重复m次的n的位置;可接受一个二元谓词 |
对于search(),从C++17开始,它有一个可选参数允许指定要使用的搜索算法:
default_searcher:普通搜索boyer_moore_searcher:实现Boyer-Moore算法的搜索boyer_moore_horspool_searcher:实现Boyer-Moore-Horspool算法的搜索
这些搜索算法在<functional>中定义。后两个算法都是针对在一大块文本中查找子字符串实现的,BMH算法虽然比BM的固定开销少,但在最坏情况下复杂度比BM高,因此要看情况选择算法。这里有个例子:
string text{ "This is the haystack to search a needle in" };
string target{ "needle" };
boyer_moore_searcher searcher{ cbegin(target), cend(target) };
auto res{ search(cbegin(text), cend(text), searcher) };
if (res != cend(text))
{
cout << "Found target!!";
}比较算法
可通过4种不同的方法比较整个范围内的元素:equal(),mismatch(),lexicographical_compare()和lexicographical_compare_three_way() [C++20]。这些算法的好处是 可以比较不同容器内的范围,因此相同类型容器元素的比较,还是用==和<运算符比较就行。
| 算法 | 解释 |
|---|---|
equal() | 如果所有对应元素都相等,就返回true;接收4个迭代器,表示两容器的范围。 |
mismatch() | 逐个元素比较两个范围是否相等或是否在二元谓词指定的意义上等效,并找到出现不同的第一个位置。 |
lexicographical_compare() | 逐个元素比较两个序列以确定其中的较小序列,如果第一个序列小于第二个,就返回true |
lexicographical_compare_three_way() | 和上一个相似,但它执行C++20的三路比较操作,并返回一个比较类别类型 |
计数算法
| 算法 | 解释 |
|---|---|
all_of() | 当给定范围中的每个元素均满足条件时返回 true。 |
any_of() | 当指定元素范围中至少有一个元素满足条件时返回 true。 |
none_of() | 当给定范围中没有元素满足条件时返回 true。 |
count() | 返回范围中其值与指定值匹配的元素的数量。 |
count_if() | 返回范围中其值与指定条件匹配的元素的数量。 |
修改序列算法
标准库提供了多种修改序列算法。一些修改算法涉及源范围和目标范围的概念,例如copy();其他算法则就地执行操作,例如generate()算法。
需要注意的是:修改算法不能将元素插入目标范围中。仅可重写/修改目标范围中已经存在的元素。因此诸如map,multimap等不能直接用修改算法,而需要 插入迭代器适配器 的帮助(详见上一篇文章)。并且,部分算法会返回一个指向输出序列最后一个元素的下一个位置的迭代器。
生成 generate
generate()算法需要一个迭代器范围,能把该范围内的值替换为从可调用对象中返回的值:
vector<int> iVec(10);
int value{ 1 };
generate(begin(iVec), end(iVec), [&value] {value *= 2; return value; });输出结果如下:
2 4 8 16 32 64 128 256 512 1024填充 fill
fill()可以将一个序列中的所有元素设置为一个新值。
fill_n()可以将一个序列中的前n个元素设置为一个新值。
变换 transform
transform()算法有多种重载,其中之一是对范围内的每个元素应用回调,期望回调生成一个新元素,并保存在指定的目标范围中。例如下面的代码将vector中每个元素增加100:
vector<int> iVec{ 1, 2, 3, 4, 5 };
transform(begin(iVec), end(iVec), begin(iVec), [](int elem)
{
return elem + 100;
});输出结果如下:
101 102 103 104 105transform()另外一种形式是对范围内的元素调用二元函数,需要将第一个范围的首尾迭代器,第二个范围的首迭代器和目标范围的首迭代器作为参数。例如下边的代码就是计算两个vector元素对的和,并将结果保存到输出流迭代器中:
vector<int> iVec1{ 1, 2, 3, 4, 5 };
vector<int> iVec2{ 2, 1, 0 };
transform(begin(iVec2), end(iVec2), begin(iVec1), ostream_iterator<int>{cout, " "},
[](int v1, int v2) { return v1 + v2; });注意,第一个容器的范围一定要比第二个的范围小,否则会报越界错误。输出结果如下:
3 3 3拷贝 copy
copy()算法可将一个范围内的所有元素复制到另一个范围中。源范围和目标范围必须不同,但在一定限制条件下可以重叠。限制条件如下:
对于copy(b, e, d),
- 如果d在b之前,则可以重叠
- 如果d处于[b, e)范围,则行为不确定(UB)
下例将vec1中的元素拷贝到vec2中,并将结果拷贝到输出流中输出(注意对vec2应用了resize()方法,因为 复制不会创建或扩大容器,只是替换现有元素):
vector<int> iVec1{ 1, 2, 3, 4, 5 };
vector<int> iVec2;
iVec2.resize(size(iVec1));
copy(cbegin(iVec1), cend(iVec1), begin(iVec2));
copy(cbegin(iVec2), cend(iVec2), ostream_iterator<int>{cout, " "});copy_backward()算法可将源范围内的元素反向复制到目标范围。也就是说,该算法从源范围最后一个元素开始,将该元素复制到目标范围的最后一个位置,并逐渐反向移动。该算法也有两个范围的限制条件:
对于copy_backward(b, e, d),
- 如果d在e之后,则能正确重叠
- 如果d处于[b, e)范围,则行为不确定(UB)
下例将vec1的元素反向拷贝到vec2中,结果和上边copy()是一样的:
// 注意第三个参数是end()
copy_backward(cbegin(iVec1), cend(iVec1), end(iVec2));copy_if()算法除了要提供copy()的三个参数,还要提供一个满足条件(可调用对象)。下例将vec1中的偶数元素复制到vec2中,并 删除vec2多余的空间:
vector<int> iVec1{ 1, 2, 3, 4, 5 };
vector<int> iVec2;
iVec2.resize(size(iVec1));
auto endIter = copy_if(cbegin(iVec1), cend(iVec1), begin(iVec2), [](int elem) { return elem % 2 == 0; });
iVec2.erase(endIter, end(iVec2));copy_n()算法从源范围中复制n个元素到目标范围。它的第一个参数是起始迭代器,第二个参数是指定要复制的元素个数,第三个参数是目标迭代器。该算法 不会执行任何边界检查,因此要确保两个范围的边界,否则会产生未定义行为。下例将vec1中复制3个元素到vec2中:
vector<int> iVec1{ 1, 2, 3, 4, 5 };
vector<int> iVec2;
iVec2.resize(3);
copy_n(cbegin(iVec1), 3, begin(iVec2));移动 move
标准库有两个移动算法move()和move_backward(),如果想在自定义类的容器里使用,得让这个类实现移动语义(移动构造函数和移动赋值运算符)。
move()有两种用法:
- 接收一个参数,将左值转换为右值,在
<utility>中定义; - 接收三个参数,在容器间移动元素。
下例用到了move()的这两个用法,先实现有移动语义的类MyClass,然后将其从vecSrc中移动到vecDst中:
class MyClass
{
public:
MyClass() = default;
MyClass(const MyClass& src) = default;
MyClass(string str) : m_str{ move(str) } {}
virtual ~MyClass() = default;
// 移动赋值运算符
MyClass& operator= (MyClass&& rhs) noexcept
{
// 自引用情况
if (this == &rhs) { return *this; }
m_str = move(rhs.m_str);
cout << format("Move operator= (m_str = {})", m_str) << endl;
return *this;
}
void setString(string str) { m_str = move(str); }
const string& getString() const { return m_str; }
private:
string m_str;
};
int main()
{
vector<MyClass> vecSrc{ MyClass{"a"}, MyClass{"b"}, MyClass{"c"} };
vector<MyClass> vecDst(vecSrc.size());
move(begin(vecSrc), end(vecSrc), begin(vecDst));
for (const auto& c : vecDst) { cout << c.getString() << " "; }
}输出结果如下:
Move operator= (m_str = a)
Move operator= (m_str = b)
Move operator= (m_str = c)
a b cmove_backward()使用和move()同样的移动机制,但按从最后一个元素向第一个元素的顺序移动。
替换 replace
replace()和replace_if()算法将一个范围内匹配某个值或满足某个谓词的元素替换为新的值。
对于replace_if(),前两个参数指定容器元素的范围,第三个参数是一个返回布尔值的lambda表达式,第四个参数则指定满足条件要替换的值。下例将容器中所有奇数值替换为0:
vector<int> vec{ 1, 2, 3, 4, 5 };
replace_if(begin(vec), end(vec), [](int elem) {return elem % 2 != 0; }, 0);
copy(cbegin(vec), cend(vec), ostream_iterator<int>{cout, " "});此外,还有名为replace_copy()和replace_copy_if()的变体,这些变体将结果复制到不同的目标范围。
擦除 erase
C++20对几乎所有标准库容器都支持std::erase()和std::erase_if()。官方将这些操作称为统一容器擦除,前者删除容器中与给定值匹配的所有元素;后者则删除与给定谓词匹配的所有元素。注意这些算法需要容器的引用,而不是迭代器的范围。从C++20开始,这些函数是删除容器中元素的首选方法。
例如下例将删除vector<string>中的所有空元素:
void removeEmpty(vector<string>& strings)
{
erase_if(strings, [](const string& str) {return str.empty(); });
}
int main()
{
vector<string> strings{ "", "2", "3", "4" };
copy(cbegin(strings), cend(strings), ostream_iterator<string>{cout, " "});
cout << endl;
removeEmpty(strings);
copy(cbegin(strings), cend(strings), ostream_iterator<string>{cout, " "});
cout << endl;
}输出如下:
2 3 4
2 3 4需要注意的是,erase_if()适用于所有容器,而erase()则不适用于有序和无序的关联容器(set/map等),因为它们有自己的erase(key)方法。
删除 remove
如果编译器还不支持C++20,那么一种可能的解决方法是这样的:
void removeEmptyOld(vector<string>& strings)
{
for (auto iter{begin(strings)}; iter != end(strings);)
{
if (iter->empty())
iter = strings.erase(iter);
else
++iter;
}
}这种方案效率很低,因为要保持vector在内存中的连续性,会涉及很多内存操作,得到\(O(n^2)\)的复杂度。
这里有一种线性时间(\(O(n)\)复杂度)的方法:“删除-擦除法(Remove-Erase-Idiom)”,这种算法只能访问迭代器抽象,不能真正地从底层容器中删除元素,而是将匹配给定值/谓词要求的元素替换为下一个不匹配的元素。最终按顺序留下两种集合:一个是要保留的元素集合;另一个是要删除的元素集合。
使用remove_if()参考实现如下:
void removeEmptyByREI(vector<string>& strings)
{
auto it{ remove_if(begin(strings), end(strings), [](const string& str) {return str.empty(); }) };
strings.erase(it, end(strings));
}remove()函数系列是稳定的,它们保持了容器中剩余元素的顺序,尽管这些算法将要保留的元素向前移动了。除了remove(),remove_if()外,也有remove_copy()和remove_copy_if()变体,它们不会改变源范围,而是将所有要保留的元素复制到另一个目标范围中。
唯一化 unique
unique()可看作特殊的remove(),它能将所有重复的连续元素删除。通常应对有序序列使用unique(),但它也能用于无序序列。并且list容器有自己的.unique()方法。
unique()的基本形式是就地操作数据,但unique_copy()则将结果复制到一个新的目标范围。
乱序 shuffle
shuffle()以随机顺序重新安排某个范围内的元素,其复杂度为线性时间,可用于洗牌等任务。它的参数是要乱序的范围的首尾迭代器,以及一个随机的随机数生成器对象。
下例展示如何设置一个随机数种子,并声明一个默认随机数生成器供我们使用shuffle():
random_device seeder;
const auto seed{ seeder.entropy() ? seeder() : time(nullptr) };
default_random_engine engine{ static_cast<default_random_engine::result_type>(seed) };
shuffle(begin(iVec), end(iVec), engine);在C++11中有个
random_shuffle()算法,它使用默认随机数生成器std::rand()生成随机数。为了让我们对shuffle()更有控制权(控制随机数生成的算法等),在C++17中该算法最终被删除。
采样 sample
sample()算法从给定的源范围返回n个随机选择的元素,并存储在目标范围。它需要五个参数:
- 采样范围的首尾迭代器
- 目标范围的首迭代器
- 要选择的元素数量
- 随机数生成引擎
例子如下:
sample(cbegin(values), cend(values), begin(target), numberOfSamples, engine);反转 reverse
reverse()算法反转某个范围内元素的顺序。将第一个元素和倒一个元素交换,以此类推。
例子如下:
reverse(begin(values), end(values));旋转 rotate
rotate()算法用于“旋转”容器中的元素,它接收三个迭代器参数:first,middle和last,然后rotate()函数将范围[first, last)中的元素进行旋转操作,将范围[first, middle)的元素移到范围[middle, last)的后面。
下例简要使用rotate()算法:
vector<string> values{ "first", "middle", "last" };
printElem(values);
rotate(begin(values), begin(values) + 1, end(values));
printElem(values);输出如下:
first middle last
middle last first移动 shift
C++20还引入了shift_left()和shift_right()算法来移动给定范围内的元素,将它们移动到新位置。位于范围两端的元素会被删除。shift_left返回指向新范围末尾的迭代器,而shift_right()则返回指向新范围开头的迭代器。
使用这两个算法的示例如下:
vector<int> values{ 11, 22, 33, 44, 55 };
printElem(values);
// 左移所有元素2位
auto newEnd{ shift_left(begin(values), end(values), 2) };
// 重设容器大小
values.erase(newEnd, end(values));
printElem(values);
// 右移所有元素2位
auto newBegin{ shift_right(begin(values), end(values), 2) };
values.erase(begin(values), newBegin);
printElem(values);输出如下:
11 22 33 44 55
33 44 55
33操作算法
此类算法只有两个:for_each()和for_each_n()。for_each()对范围内的每个元素执行回调,for_each_n()对范围内的前n个元素执行回调。如果给定迭代器的类型是非const,则回调可以修改范围内的元素。
for_each()
下例用for_each()和lambda表达式,计算范围内元素的和与积:
vector<int> values{ 11, 22, 33, 44, 55 };
int sum{ 0 };
int product{ 1 };
for_each(cbegin(values), cend(values), [&sum, &product](int i)
{
sum += i;
product *= i;
});
cout << format("Sum: {}", sum) << endl;
cout << format("Product: {}", product) << endl;也能用仿函数实现这个功能:
class SumAndProduct
{
public:
void operator() (int value)
{
m_sum += value;
m_product *= value;
}
int getSum() const { return m_sum; }
int getProduct() const { return m_product; }
private:
int m_sum{ 0 };
int m_product{ 1 };
};
// main
SumAndProduct calc;
calc = for_each(cbegin(values), cend(values), calc);
cout << calc.getSum() << " " << calc.getProduct();可以发现这里用了for_each()的返回值,它返回calc经过std::move()的结果,如果calc没有实现移动语义(本例),就会返回一个它的拷贝。
for_each_n()
for_each_n()算法需要范围的起始迭代器、要迭代的元素数量以及函数回调。它返回的迭代器等于begin + n,通常不执行任何边界检查。
下例迭代map的前两个元素:
map<int, int> myMap{{1, 10}, {2, 20}, {3, 30}};
for_each_n(cbegin(myMap), 2, [](const auto& p)
{
cout << p.first << ", " << p.second << endl;
});交换算法
iter_swap()
交换给定的迭代器所指向的元素的值。
swap_ranges()
接收第一个范围的首尾迭代器和第二个范围的首迭代器,将这两个范围间的元素进行交换。
分区算法
如果谓词返回true的所有元素在谓词返回false的所有元素之前,则序列将根据某个谓词对序列进行分区。序列中不满足谓词的第一个元素被称为分区点(Partition Point)。
partition()
该算法对序列进行不稳定分区。下例演示了如何把vector分为偶数在前,奇数在后的分区:
vector<int> values{1, 2, 3, 4, 5, 6};
printElem(values);
partition(begin(values), end(values), [](int elem) {return elem % 2 == 0; });
printElem(values);输出如下:
1 2 3 4 5 6
6 2 4 3 5 1partition_copy()
该算法将来自某个来源的元素复制到两个不同的目标,因此它会 返回一对迭代器:指向第一个和第二个目标范围内最后一次拷贝元素的迭代器。
下例在上例的基础上,将奇数和偶数分开存储:
vector<int> values{1, 2, 3, 4, 5, 6};
printElem(values);
vector<int> odds(values.size()), evens(values.size());
auto pairIters{ partition_copy(cbegin(values), cend(values), begin(evens), begin(odds),
[](int i) {return i % 2 == 0; }) };
evens.erase(pairIters.first, end(evens));
odds.erase(pairIters.second, end(odds));
printElem(evens);
printElem(odds);输出如下:
1 2 3 4 5 6
2 4 6
1 3 5除此之外,还有几个分区算法:is_partitioned(),stable_partition()和partition_point()没说,这里待补全或者自行去微软开发者文档查找。
排序算法
标准库还提供了一些不同的排序方法,它只能应用于顺序容器。排序和有序关联容器(set/map)无关,因为有序关联容器已经维护了元素的顺序;排序也和无序关联容器(unordered_xxx)无关,因为它们没有排序的概念。而一些容器(list和forward_list等)也有自己特化的高效排序算法。因此,通用的排序算法最适用于 vector, deque, array 和 C风格数组。
sort()
sort()算法一般情况下在\(O(N\log N)\)时间内对某个范围的元素进行排序。sort()默认根据operator<进行排序,即进行升序排序。也能通过添加一个可调用对象实现自定义规则排序。
stable_sort()是该算法的变体,可以保证范围内相等元素的相对顺序,因此效率也相对低了。
is_sorted()可以检查指定范围内元素是否有序;is_sorted_until()则返回一个迭代器,该迭代器之前的元素都是有序的。
nth_element()
nth_element()是一个强大的选择算法,给定一个元素范围和一个指向该范围内第n个元素的迭代器,该算法会重新排列该范围内的元素,并且第n个元素就是刚刚给定的那个元素,时间复杂度是\(O(n)\)。
下例使用nth_element(),找出第三大的元素:
vector<int> values{1, 2, 3, 4, 5, 6};
nth_element(begin(values), begin(values) + 2, end(values), greater<>{});
cout << values.at(2);结果是4。
也可以结合sort()使用,例如要获取5个最大的元素:
vector<int> values{1, 2, 3, 4, 5, 6};
// 先分区
nth_element(begin(values), begin(values) + 4, end(values), greater<>{});
printElem(values);
// 再排序前5大的元素(begin+5的原因是参数end要求指向第5个元素的下一个)
sort(begin(values), begin(values) + 5);
for_each_n(begin(values), 5, [](const auto& elem) {cout << elem << " "; });结果如下:
6 5 4 3 2 1
2 3 4 5 6除此之外,还有partial_sort()和partial_sort_copy(),它们只排序范围中的部分元素,其余不排序,并看要求修改源范围/复制到新范围。
二分搜索算法
这种算法通常用于 有序序列或至少已分区的序列。一些关联容器(map/set)有它们特化的高效算法,应该使用这些成员方法而不是接下来要说的通用算法。
lower_bound()
STL源码中的原话:找到第一个可以插入
__val的位置,并且不改变原有排序(Finds the first position in which@a valcould be inserted without changing the ordering.)。
该算法在有序范围内查找不小于(大于等于)给定值的第一个元素,常用于发现在有序序列中将新值插入那个位置,使插入后序列仍有序。
auto iter { lower_bound(begin(values), end(values), number) };
values.insert(iter, number);upper_bound()
STL源码中的原话:找到最后一个可以插入
val而不改变原来有序数组的排序位置(Finds the last position in which@p __valcould be inserted without changing the ordering)。
查找有序序列中大于给定值的第一个元素。
equal_range()
返回一对pair,包含上边lower_bound()和upper_bound()的结果。
binary_search()
该算法以对数时间搜索元素,需要指定范围的首尾迭代器、要搜索的值和可选的比较回调,结果是一个布尔值,找到是true。注意:如果sort()/partition()有比较回调,那么该算法的比较回调也需和sort()/partition()的比较回调一致。
集合算法
集合算法可用于任意有序范围,它是一种特殊的修改算法,最适合操作set容器的序列,当然也能操作大部分容器的 排序后 序列。
includes()
includes()算法实现了标准的子集判断功能,检查某个有序范围内的所有元素是否包含在另一个有序范围内。
if (includes(cbegin(vec1), cend(vec1), cbegin(vec2), cend(vec2)))
{
cout << "Vec2是Vec1的子集" << endl;
}set_xxx()
这些算法实现了标准的集合操作,给定两个有序序列,进行集合操作后,将结果复制到第三个排好的序列中。详见下表:
| 算法 | 释义 | 结果范围 |
|---|---|---|
set_union() | 两集合取并集 | 两个输入范围的总和 |
set_intersection() | 两集合取交集 | 两个输入范围的最小大小 |
set_difference() | 两集合取差集(只存在于第一个集合,不存在于第二个集合) | 第一个输入范围的大小 |
set_symmetric_difference() | 两集合取对称差集(两个集合的“异或”,所有存在于其中一个集合但不同时存在于两集合的元素) | 两个输入范围的总和 |
// 并集
result.resize(size(vec1) + size(vec2));
auto newEnd {set_union(cbegin(vec1), cend(vec1), cbegin(vec2), cend(vec2), begin(result))};
// Ps: 实际上插入位置begin(result)还是有点危险, 应该用<iterator>中
// 的std::inserter(容器, 迭代器位置);
// 例: std::inserter(result, result.begin());merge()
merge()算法可将两个排好序的范围归并在一起,并维持排好的顺序复制到一个新范围里(如果想就地归并,需要用implace_merge()算法)。这个算法的复杂度为线性时间,需要以下参数:
- 第一个源范围的首尾迭代器
- 第二个源范围的首尾迭代器
- 目标范围的起始迭代器,目标范围得足够大,以保存归并后的结果。
- (可选)比较回调
vecMerged.resize(size(vecA) + size(vecB));
merge(cbegin(vecA), cend(vecA), cbegin(vecB), cend(vecB), begin(vecMerged));堆算法
堆是一种标准的数据结构,数组或序列中的元素以半排序方式在其中,因此能够快速找到“堆顶”元素。例如priority_queue这种结构就是用堆实现的,也用到了堆算法。常见的堆算法如下:
| 算法 | 解释 |
|---|---|
is_heap() | 检查某范围内元素是不是堆 |
is_heap_until() | 在给定范围的元素中查找最大的子堆 |
make_heap() | 从某范围中创建一个堆 |
push_heap(), pop_heap() | 在堆中添加/删除元素 |
sort_heap() | 对堆进行升序排序 |
最小/最大算法
min()/max()
通过运算符operator<或用户提供的二元谓词比较两个或多个任意类型的元素,并返回一个较小/较大元素的const引用。
// 比较两个数
int max = max(x, y);
// 比较一堆数字(用到初始化列表)
int max = max({x, y, z, w});在GNU C Library(glibc)有宏MIN()和MAX();在Windows.h中有宏min()和max()。为了避免误用这些宏导致二次计算,可以这样使用:
auto maxValue = {(std::max)(1, 2)};在Windows上,可以在添加Windows.h前添加
#define NOMINMAX来禁用Windows的min()和max()宏。
minmax()
以pair的形式返回包含两个或多个元素的最大和最小值。
// 使用minmax()
auto p {minmax({x, y, z, w})};
cout << format("Minmax of 4 elements is <{},{}>", p.first, p.second) << endl;
// 使用minmax() + C++17结构化绑定
auto[min1, max1] {minmax({x, y, z, w})};
cout << format("Minmax of 4 elements is <{},{}>", min1, max1) << endl;min_element()/max_element()
处理迭代器范围的min/max问题。
minmax_element()
处理迭代器范围的minmax问题,返回一对包含指向最小和最大元素的迭代器。
clamp()
是一个小型辅助函数,在<algorithm>中定义,可用于确保值v在给定的最小值lo和最大值hi之间:
- 如果v < lo,返回对lo的引用
- 如果v > hi,返回对hi的引用
- 否则返回对v的引用
例如:
clamp(-3, 1, 10); // 1
clamp(3, 1, 10); // 3
clamp(22, 1, 10); // 10并行算法
当处理大型数据集或必须对数据集中的每个单独元素进行大量工作时,可使用算法的并行版本来提高性能。目前有约60中算法支持并行执行,它需要接受一个执行策略作为第一个参数,执行策略共有4个,定义在<execution>中:
| 执行策略 | 全局实例 | 描述 |
|---|---|---|
sequenced_policy | seq | 不允许算法并行执行 |
parallel_policy | par | 允许算法并行执行 |
parallel_unsequenced_policy | par_unseq | 允许算法并行执行和矢量化执行,还允许在线程间迁移执行 |
unsequenced_policy 【C++20】 | unseq | 允许算法矢量化执行,但不允许并行执行 |
当编译器矢量化代码时,会用一个所谓的矢量CPU指令替换多个CPU指令。矢量指令用一条硬件指令对多个数据执行一些操作,这种指令也被称为 单指令多数据指令(SIMD)。
首先是parallel_policy,使用并行策略对vector容器排列的实例如下:
vector<int> values{1, 2, 3, 4, 5, 6};
sort(execution::par, begin(values), end(values), greater<>{});需要注意的是,传递给并行算法的回调函数不允许抛出任何未捕获的异常,否则会调用std::terminate()终止程序。
然后是支持矢量化的parallel_unsequenced_policy和unsequenced_policy,它们允许对回调函数进行交错调用,即不按顺序执行。这意味着会对函数回调施加诸多限制:不能分配/释放内存,获取互斥以及使用非锁std::atomic等。
以下还有些要注意的点:
- 并行算法未采取措施避免数据争用和死锁,需要程序员自行解决。
- 即使非并行算法是
constexpr,但并行版本的算法不是。 - 与非并行版本相比,某些并行版本算法的返回类型可能略有不同。例如
for_each(),非并行返回提供的回调,而并行则没有返回任何东西。
数值处理算法
前面已经介绍了accumumate()算法,接下来康康其他的数值处理算法:
iota()
<numeric>定义的iota()算法会生成指定范围内的序列值,从给定的值开始,调用operator++生成每个后续值:
iota(begin(values), end(values), 5);reduce算法
标准库有4种reduce算法:accumulate(), reduce(), inner_product()和transform_reduce(),它们都定义在<numeric>中。
accumulate()
之前已经介绍过了,它不支持并行处理。
reduce()
该算法和accumulate()差不多,都是计算广义和,但它支持并行和矢量化运行。
int res = std::reduce(std::execution::par_unseq, cbegin(vec), cend(vec));有关广义和的定义:
计算\([X_0,X_n]\)内元素的和,初始值为Init,并且给定了二元运算符\(\Theta\):\(\mathrm{Init}\ \Theta\ X_0\ \Theta\ ...\ \Theta\ X_{n-1}\)。
默认情况下,
accumulate()的二元运算符是operator+,reduce()的二元运算符是std::plus。
inner_product()
该算法计算两个序列的内积(\((X_1Y_1)+(X_2Y_2)+...\)):
int res = inner_product(cbegin(v1), cend(v1), cbegin(v2), 0);它需要两个二元运算符,默认情况下分别是operator+和operator*。inner_product()不支持并行执行,如果要并行执行,得用下面提到的transform_reduce()。
transform_reduce()
该算法支持并行执行,有两个版本:
- 应用于一个范围,计算\([X_0,X_n]\)内应用一元函数\(f\)的广义和:\(\mathrm{Init}\ \Theta\ f(X_0)\ \Theta\ ...\ \Theta\ f(X_{n-1})\)
- 应用于两个范围,行为和
inner_product()相同,使用二元运算符std::plus和std::multiplies。
扫描算法(前缀和)
首先是exclusive_scan(),inclusive_scan()和partial_sum(),它们计算前缀和如下表(partial_sum()的init为0):
exclusive_scan() | inclusive_scan()/partial_sum() |
|---|---|
| \(\mathrm{y_0=Init}\) | \(\mathrm{y_0=Init\ \Theta\ X_0}\) |
| \(\mathrm{y_1=Init\ \Theta\ X_0}\) | \(\mathrm{y_1=Init\ \Theta\ X_0\ \Theta\ X_1}\) |
| \(\mathrm{y_2=Init\ \Theta\ X_0\ \Theta\ X_1}\) | … |
| … | … |
| \(\mathrm{y_{n-1}=Init\ \Theta\ X_0\ \Theta\ X_1\ ...\ \Theta\ X_{n-2}}\) | \(\mathrm{y_{n-1}=Init\ \Theta\ X_0\ \Theta\ X_1\ ...\ \Theta\ X_{n-1}}\) |
然后是transform_exclusive_scan()和transform_inclusive_scan(),在计算广义和之前,都给X应用一个一元函数。
这些扫描算法除了partial_sum()都能并行计算。
基于范围库的约束算法
在C++20中,大多数算法在std::ranges名称空间中都有所谓的受约束版本。【TODO:学习C++20范围库的基本用法】
参考资料
- 飘零的落花 - 现代C++详解
- C++20高级编程