1 - 贪心入门

发表于 2024-05-13 更新于 2024-05-14 分类于 cpp ，数据结构与算法， 6-贪心阅读次数： Waline：本文字数： 4.5k 阅读时长 ≈ 4 分钟

贪心问题入门。

区间问题

区间选点

905. 区间选点 - AcWing题库

确定贪心算法：

将每个区间按照右端点从小到大排序。
从前往后一次枚举每个区间：
1. 当前区间已经包含点，直接枚举下个区间
2. 否则选择当前区间的右端点

证明贪心算法正确性：

对于要的答案ans，必然是可行解cnt的最小值，有ans <= cnt。
对于极端情况（区间无交集），至少需要cnt才是可行解，有ans >= cnt。

因此有ans = cnt，即贪心算法的局部最优解就是全局最优解。

参考代码如下：

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

struct Seg
{
    int left, right;
    
    bool operator< (const Seg& rhs) const
    {
        return right < rhs.right;
    }
    
    Seg(int left, int right) : left(left), right(right) {}
};

int main()
{
    int n;
    cin >> n;
    
    vector<Seg> segs;
    for (int i = 0; i < n; ++i)
    {
        int left, right;
        cin >> left >> right;
        segs.emplace_back(left, right);
    }
    
    // 贪心算法
    sort(segs.begin(), segs.end());
    int ans = 0, pos = -2e9;
    for (auto& seg : segs)
    {
        if (pos < seg.left)
        {
            pos = seg.right;
            ++ans;
        }
    }
    cout << ans;
}

最大不相交区间数量

908. 最大不相交区间数量 - AcWing题库

和上题一模一样。

区间分组

906. 区间分组 - AcWing题库

确定贪心算法：

将每个区间按照左端点从小到大排序。
从前往后一次枚举每个区间：

判断能否将其放到某个现有的组中（当前区间左端点 <= 组中最右端点）：
- 如果不存在这样的组，就开个新组，将其放进新组
- 如果存在这样的组，将其放入这个组，然后更新这个组的最右端点

参考代码如下：

#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;

struct Seg
{
    int left, right;
    
    bool operator< (const Seg& rhs) const
    {
        return left < rhs.left;
    }
    
    Seg(int left, int right) : left(left), right(right) {}
};

const int INF = 2e9;

int main()
{
    int n;
    cin >> n;
    
    vector<Seg> segs;
    for (int i = 0; i < n; ++i)
    {
        int left, right;
        cin >> left >> right;
        segs.emplace_back(left, right);
    }
    
    // 贪心算法
    sort(segs.begin(), segs.end());
    priority_queue<int, vector<int>, greater<int>> maxR;
    for (auto& seg : segs)
    {
        if (maxR.empty() || maxR.top() >= seg.left)
            maxR.push(seg.right);
        else
        {
            maxR.pop();
            maxR.push(seg.right);        
        }
    }
    cout << maxR.size();
}

区间覆盖

907. 区间覆盖 - AcWing题库

令被覆盖的区间范围为[start, end]，确定贪心算法：

将每个区间按照左端点从小到大排序。
从前往后依次枚举每个区间：

在所有能覆盖start的区间中，选择右端点最大的区间。

选完后将start更新为该区间的右端点。

参考代码如下：

#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;

struct Seg
{
    int left, right;

    bool operator< (const Seg& rhs) const
    {
        return left < rhs.left;
    }

    Seg(int left, int right) : left(left), right(right) {}
};

const int INF = 2e9;

int main()
{
    int st, ed, n;
    cin >> st >> ed >> n;

    vector<Seg> segs;
    for (int i = 0; i < n; ++i)
    {
        int left, right;
        cin >> left >> right;
        segs.emplace_back(left, right);
    }

    // 贪心算法
    sort(segs.begin(), segs.end());
    int ans = 0;
    bool isOK = false;
    for (int i = 0; i < n; ++i)
    {
        int j = i, maxR = -INF;
        while (j < n && segs[j].left <= st)
        {
            maxR = max(maxR, segs[j].right);
            j++;
        }

        // 无解
        if (maxR < st)
        {
            isOK = false;
            break;
        }

        // 有解
        ans++;
        if (maxR >= ed)
        {
            isOK = true;
            break;
        }

        st = maxR;
        i = j - 1;
    }

    if (isOK)
        cout << ans;
    else
        cout << -1;
}

Huffman树

获取答案的过程是一棵Huffman树：

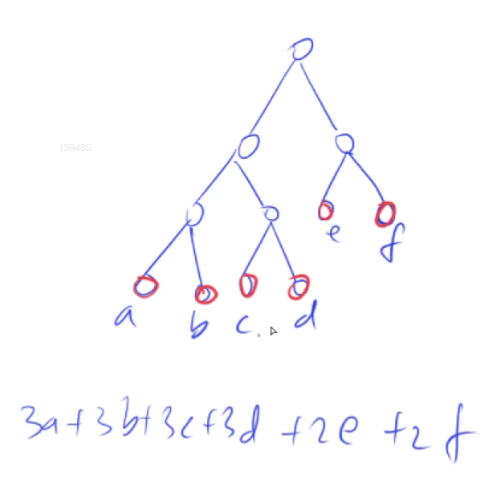
合并果子

148. 合并果子 - AcWing题库

只需要每次合并重量最小的两堆果子就行了。

#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;

int main()
{
    int n;
    cin >> n;
    priority_queue<int, vector<int>, greater<int>> heap;
    
    for (int i = 0; i < n; ++i)
    {
        int x;
        cin >> x;
        heap.push(x);
    }
    
    int ans = 0;
    while (heap.size() > 1)
    {
        int a = heap.top(); heap.pop();
        int b = heap.top(); heap.pop();
        ans += a + b;
        heap.push(a + b);
    }
    cout << ans;
}

排序不等式

形如f(x) = e1 * w1 + e2 * w2, ...的最值问题。

排队打水

913. 排队打水 - AcWing题库

让耗费时间少的人先打水，这样花费所有人的时间会最少：

时间为1的人打水，剩余人等待 6 * 1；
时间为2的人打水，剩余人等待 5 * 2；
时间为3的人打水，剩余人等待 4 * 3；
…

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int main()
{
    int n;
    cin >> n;
    vector<int> t(n);
    for (int i = 0; i < n; ++i)
        cin >> t[i];
    
    sort(t.begin(), t.end());
    
    long long res = 0;
    for (int i = 0; i < n; ++i)
        res += t[i] * (n - i - 1);
    
    cout << res;
}

绝对值不等式

形如f(x) = |x1 - x| + |x2 - x| + ...的最值问题。

可以将这些选项分组，有：

f(x) = (|x1 - x| + |xn - x|) + (|x2 - x| + |xn-1 - x|) + ...。

如果我们要求f(x)的最小值，例如第一组，x都应尽量位于[x1, xn]之间，此时每组路径和为xn - x1。最稳妥的做法就是取它们的中位数。

货舱选址

104. 货仓选址 - AcWing题库

对商店从小到大排序后，取它们中点即可，然后求距离之和。

参考代码如下：

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int main()
{
    int n;
    cin >> n;
    vector<int> a(n);
    for (int i = 0; i < n; ++i)
        cin >> a[i];
    
    sort(a.begin(), a.end());
    
    int res = 0;
    for (int i = 0; i < n; ++i)
        res += abs(a[i] - a[n / 2]);
    cout << res;
}

推公式

题中推出来的公式 + 不等式解决贪心问题。

耍杂技的牛

125. 耍杂技的牛 - AcWing题库

要使每头牛的危险值最小，根据贪心思想：

自身w值越大应该放到底部（即减小上述式中的被减数）
自身s值越大应该放到底部（即增大上述式中的减数）

因此按照 w[i] + s[i] 从小到大的顺序排序，最大的危险系数一定是最小的。

参考代码如下：

#include <iostream>
#include <algorithm>
using namespace std;

typedef pair<int, int> PII;
const int N = 50010;
int n;
PII cow[N];
int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ )
    {
        int s, w;
        scanf("%d%d", &w, &s);
        cow[i] = {w + s, w};
    }

    sort(cow, cow + n);

    int res = -2e9, sum = 0;
    for (int i = 0; i < n; i ++ )
    {
        int s = cow[i].first - cow[i].second, w = cow[i].second;
        res = max(res, sum - s);
        sum += w;
    }

    printf("%d\n", res);

    return 0;
}