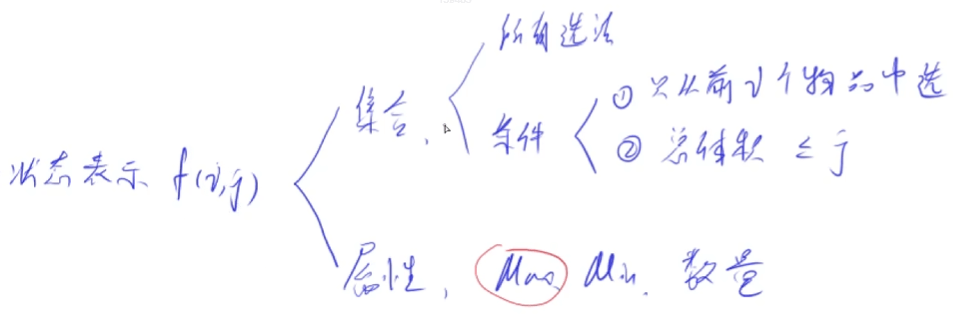3 - 背包问题

发表于 2024-05-07 更新于 2024-05-08 分类于 cpp ，数据结构与算法， 5-动态规划阅读次数： Waline：本文字数： 10k 阅读时长 ≈ 8 分钟

非常哈人动态规划，使我脑子旋转。

背包问题

0/1背包问题

概念

给N个物品，一个容量为V的背包，物品有它的体积Vi和价值Wi。每个物品最多使用一次，求能放入背包物品的最大总价值。

思路

使用动态规划解决问题，要思考两大点：

状态表示：整个问题需要用几维的状态来表示，每维状态的含义是什么，以及要求的是最大值、最小值还是数量。

如图，01背包问题可用二维集合f(i, j)表示，含义是所有选法的价值的最大值。

其中，每个维的含义如下：
- i表示只从前i个物品选；
- j表示选择的物品总体积 <= j。
例如，f(2, 3)就是求在只选择前2个物品，总体积不超过3的选法中，物品总价值的最大值。

该问题的最终答案是f(N, V)。
状态计算(求状态转移方程)：就是如何将集合f(i, j)划分为可计算的子集合。
划分子集的原则：
- 不重复：划分的子集合不能属于两个父集合，这个原则有时候可以忽略。
- 不遗漏：所有子集合都需要被考虑到。
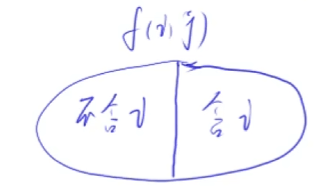
如图，f(i, j)可被划分为不选i，选i两个子集合：
- 不选i，也就是f(i - 1, j)，从1 ~ i-1中选，并且总体积不超过j。
- 选i，也就是f(i - 1, j - Vi)，从1 ~ i-1中选，并且总体积不超过j-Vi（给i留坑），然后再加上Wi。需要注意的是，选i的前提是当前体积j可以放下Vi。
最终f(i, j)只需要取两个子集合的最大值就行了：f(i, j) = max(f(i - 1, j), f(i - 1, j - Vi) + Wi)。

代码实现

2. 01背包问题 - AcWing题库

朴素版

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

struct Stuff
{
    int v, w;
    Stuff(int volume, int weight) : v(volume), w(weight) {}
};

int main()
{
    int n, v;
    cin >> n >> v;

    vector<Stuff> stuffs(n + 5, Stuff(0, 0));
    for (int i = 1; i <= n; ++i)
    {
        cin >> stuffs[i].v >> stuffs[i].w;
    }

    // 动态规划
    vector<vector<int>> dp(n + 5, vector<int>(v + 5, 0));
    // i是编号, 从1到n
    for (int i = 1; i <= n; ++i)
    {
        // j是背包容量, 从0到v
        for (int j = 0; j <= v; ++j)
        {
            // 还要考虑能不能装下i
            if (j >= stuffs[i].v)
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - stuffs[i].v] + stuffs[i].w);
            else
                dp[i][j] = dp[i - 1][j];
        }
    }


    cout << dp[n][v];
}

一维优化版

动态规划的优化一般都是对代码/状态转移方程做等价变形。例如这里f(i, j)中的i只用到了i - 1；j却用到j和j - Wi，均<= j，因此能用一维滚动数组进行空间优化，删掉i这一维。

注意到在j的枚举中，从0到stuffs[i].v是没有意义的，因此可以让j从stuffs[i].v ~ V枚举，然后代码就成了这样：

for (int i = 1; i <= n; ++i)
	for (int j = stuffs[i].v; j < v; ++j)
        dp[j] = max(dp[j], dp[j - stuffs[i].v] + stuffs[i].w);

但这样写仍有问题，就是dp[j - stuffs[i].v]可能在循环过程中被修改，导致结果不是期望的。为了避免在一次循环中它是1，另一次就成2了，对j的枚举应该改成从V 到stuffs[i].v逆向枚举，防止被修改：

for (int i = 1; i <= n; ++i)
	for (int j = v; j >= stuffs[i].v; --j)
        dp[j] = max(dp[j], dp[j - stuffs[i].v] + stuffs[i].w);

最后的答案是dp[V]。

完全背包问题

概念

给N个物品，一个容量为V的背包，物品有它的体积Vi和价值Wi。每个物品不限使用次数，求能放入背包物品的最大总价值。

思路

状态表示：和0/1背包问题一样，都是f(i, j)：
状态计算：对集合f(i, j)进行划分，分为：
- 第i个物品选0个：f(i - 1, j - 0 * Vi) + 0 * Wi；
- 第i个物品选1个：f(i - 1, j - 1 * Vi) + 1 * Wi；
- …
- 第i个物品选了k个：f(i - 1, j - k * Vi) + k * Wi。
而我们要这些集合的最大值。

综合起来，有f(i, j) = max(f(i - 1, j), ..., f(i - 1, j - k * Vi) + k * Wi)，也就是f(i, j) = max(f(i, j), f(i - 1, j - k * Vi) + k * Wi)。

代码实现

3. 完全背包问题 - AcWing题库

朴素版

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

struct Stuff
{
    int v, w;
    Stuff(int v, int w) : v(v), w(w) {}
};

int main()
{
    int n, v;
    cin >> n >> v;

    vector<Stuff> objs(n + 5, Stuff(0, 0));
    for (int i = 1; i <= n; ++i)
        cin >> objs[i].v >> objs[i].w;

    // dp
    vector<vector<int>> dp(n + 5, vector<int>(v + 5, 0));
    for (int i = 1; i <= n; ++i)
        for (int j = 0; j <= v; ++j)
            for (int k = 0; k * objs[i].v <= j; ++k)
                dp[i][j] = max(dp[i][j], dp[i - 1][j - k * objs[i].v] + k * objs[i].w);

    cout << dp[n][v];
}

二维优化版

将f(i, j) 和f(i, j - Vi)展开，发现：

综合得到：f(i, j) = max(f(i - 1, j), f(i, j - Vi) + w))。因此代码如下：

// dp
vector<vector<int>> dp(n + 5, vector<int>(v + 5, 0));
for (int i = 1; i <= n; ++i)
{
    for (int j = 0; j <= v; ++j)
    {
        // 枚举第一个子集合
        dp[i][j] = dp[i - 1][j];
        // 能放下就枚举第二个子集合
        if (j >= objs[i].v)
            dp[i][j] = max(dp[i][j], dp[i][j - objs[i].v] + objs[i].w);
    }
}
cout << dp[n][v];

一维优化版

按照01背包的优化思路，完全背包也能优化为1维滚动数组:

dp[i][j] = dp[i - 1][j]变为dp[j] = dp[j]，无意义可省去。
修改j的遍历区间为objs[i].v ~ v，dp[i][j] = max(dp[i][j], dp[i][j - objs[i].v] + objs[i].w)变为dp[j] = max(dp[j], dp[j - objs[i].v] + objs[i].w)。这里不需要修改j的遍历区间从大到小，是因为修改的是同一层状态，而不是上一层。

参考代码如下：

vector<int> dp(v + 5, 0);
for (int i = 1; i <= n; ++i)
    for (int j = objs[i].v; j <= v; ++j)
        dp[j] = max(dp[j], dp[j - objs[i].v] + objs[i].w);

多重背包问题

概念

有 N 种物品和一个容量是 V 的背包。第 i 种物品最多有 si 件，每件体积是 vi，价值是 wi。求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。输出最大价值。

思路

状态表示：还是f(i, j)，所有只从前i个物品中选，并且总体积不超过j的选法，我们要这些选法的最大值。
状态计算：对集合f(i, j)进行划分，有如下子集合：
- 选0个i；
- 选1个i；
- …
- 选Si个i；
可以发现和完全背包问题的状态转移方程相同，不过有了数量上限。因此多重背包问题的状态转移方程为：f(i, j) = max(f(i, j), f(i - 1, j - k * Vi) + k * Wi)，其中k = 0, 1, ..., Si。

代码实现

朴素版

4. 多重背包问题 I - AcWing题库

#include <iostream>
#include <vector>
using namespace std;

int main()
{
    int n, m;
    cin >> n >> m;
    
    vector<int> v(n + 5), w(n + 5), s(n + 5);
    for (int i = 1; i <= n; ++i)
    {
        cin >> v[i] >> w[i] >> s[i];
    }
    
    // dp
    vector<vector<int>> dp(n + 5, vector<int>(m + 5, 0));
    for (int i = 1; i <= n; ++i)
        for (int j = 0; j <= m; ++j)
            for (int k = 0; k <= s[i] && k * v[i] <= j; ++k)
                dp[i][j] = max(dp[i][j], dp[i - 1][j - k * v[i]] + k * w[i]);
        
    cout << dp[n][m];
}

二进制优化

5. 多重背包问题 II - AcWing题库

不能用完全背包的优化来优化多重背包，因为有Si限制，得另寻他法。

假设第i个物品有1023个，如果计算取0~1023个物品的所有情况就太慢了（上面的朴素版），可以将物品先“打包”，再取。例如，将物品打包为1个, 2个, 4个, 8个, …, 512个共十组，那么取0~1023个物品情况就能由通过取这十组的若干组凑出来。这样就相当于把一种多重背包问题的物体变成十种0/1背包问题的物体了。枚举次数从1024次直接降低到10次，大大提高了效率。

先来看看组该怎么划分，假设有S个物品，根据1 + 2 + ... + 2^k <= S，1 + 2 + ... + 2^k = sum, sum + (S - sum) = S，可划分出这样的k + 1组物品。

然后我们就能开始凑物品了，变成解k+1种物体的0/1背包问题了。

这是对多重背包问题的一种物品的处理方式，只需对所有物品都这样处理就行了。参考代码如下：

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int main()
{
    int n, m;
    cin >> n >> m;
    vector<int> v(1, 0), w(1, 0);
    
    // 二进制分组优化
    int cnt = 0;    // 统计分组后物品总组数
    for (int i = 0; i < n; ++i)
    {
        int vv, ww, s;
        cin >> vv >> ww >> s;
        
        // 开始给每个物品分组
        int k = 1;
        while (k <= s)
        {
            cnt++;
            v.push_back(k * vv);
            w.push_back(k * ww);
            s -= k;
            k *= 2;
        }
        // 还有剩余的, 再分一组
        if (s > 0)
        {
            cnt++;
            v.push_back(s * vv);
            w.push_back(s * ww);
        }
    }
    
    // 解0/1背包问题 (注意分组后物品总数变成了cnt)
    vector<int> dp(m + 5, 0);
    for (int i = 1; i <= cnt; ++i)
        for (int j = m; j >= v[i]; --j)
            dp[j] = max(dp[j], dp[j - v[i]] + w[i]);
            
    cout << dp[m];
}

分组背包问题

概念

有 N 组物品和一个容量是 V 的背包。每组物品有若干个，同一组内的物品最多只能选一个。每件物品的体积是 vij，价值是 wij，其中 i 是组号，j 是组内编号。求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。输出最大价值。

思路

状态表示：还是f(i, j)，只从前i组物品中选，且总体积<= j的所有选法，我们要总价值的最大值。
状态计算：前面的背包问题都是围绕第i种物品选几个，而分组背包问题则是 围绕第i组物品选哪个：
- 不选第i组的物品：f(i - 1, j)。
- 选择第i组第1个物品：f(i - 1, j - V[i][1]) + W[i][1]。
- …
- 选择第i组第Si个物品：f(i - 1, j - V[i][Si]) + W[i][Si]。
我们要这些子集的最大值。因此状态转移方程是f(i, j) = max(f(i, j), f(i - 1, j - V[i][k]) + W[i][k]))。

代码实现

9. 分组背包问题 - AcWing题库

朴素版

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int main()
{
    int n, m;
    cin >> n >> m;
    
    vector<int> s(n + 5, 0);
    vector<vector<int>> v(n + 5), w(n + 5);
    for (int i = 1; i <= n; ++i)
    {
        cin >> s[i];
        vector<int> vv(s[i] + 5, 0), ww(s[i] + 5, 0);
        for (int j = 1; j <= s[i]; ++j)
            cin >> vv[j] >> ww[j];
        v[i] = vv;
        w[i] = ww;
    }
    
    // dp
    vector<vector<int>> dp(n + 5, vector<int>(m + 5, 0));
    for (int i = 1; i <= n; ++i)
        for (int j = 0; j <= m; ++j){
            // k = 0
            dp[i][j] = dp[i - 1][j];
            // k = 1 ~ s[i]
            for (int k = 1; k <= s[i]; ++k)
                if (v[i][k] <= j)
                    dp[i][j] = max(dp[i][j], dp[i - 1][j - v[i][k]] + w[i][k]);
        }
    
    cout << dp[n][m];
}

一维优化版

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int main()
{
    int n, m;
    cin >> n >> m;
    
    vector<int> s(n + 5, 0);
    vector<vector<int>> v(n + 5), w(n + 5);
    for (int i = 1; i <= n; ++i)
    {
        cin >> s[i];
        vector<int> vv(s[i] + 5, 0), ww(s[i] + 5, 0);
        for (int j = 1; j <= s[i]; ++j)
            cin >> vv[j] >> ww[j];
        v[i] = vv;
        w[i] = ww;
    }
    
    // dp
    vector<int> dp(m + 5, 0);
    for (int i = 1; i <= n; ++i)
        for (int j = m; j >= 0; --j)       // 要用到上一层的dp, 因此倒序遍历j
            for (int k = 1; k <= s[i]; ++k)
                if (v[i][k] <= j)
                    dp[j] = max(dp[j], dp[j - v[i][k]] + w[i][k]);
    
    cout << dp[m];
}

总结

dp数组初始化问题

求最大值

数组所有元素初始化为最小值（负值），第一个元素初始化为0。求的时候是形如dp[] = max(,)的式子。

求最小值

数组所有元素初始化为最大值，第一个元素初始化为0。求的时候是形如dp[] = min(,)的式子。

求方案数

数组所有元素初始化为0，第一个元素初始化为1。求的时候是形如dp[] += dp[...]的式子。

代码“模板”

0/1背包问题

完全背包问题

多重背包问题

分组背包问题

练习题

0/1背包

2915. 和为目标值的最长子序列的长度 - 力扣（LeetCode）

0/1背包模板题。物品个数为nums.size()，背包容量为target。物品i的容量为nums[i]，价值为1。我们要取最大值。

参考代码如下：

int lengthOfLongestSubsequence(vector<int>& nums, int target) {
    int n = nums.size();
    int v = target;

    // dp: 由于要输出不存在的答案, 这里让dp初始化为负数, 然后dp[0]初始化为0
    vector<int> dp(v + 5, -114514);
    dp[0] = 0;
    for (int i = 0; i < n; ++i)
        for (int j = v; j >= nums[i]; --j)
            dp[j] = max(dp[j], dp[j - nums[i]] + 1);

    return dp[v] > 0 ? dp[v] : -1;
}

416. 分割等和子集 - 力扣（LeetCode）

这道题看起来有点吓人，实际上就是上面那道题的变种。将数组分割为等和子集，就是求和为数组总和一半的最长子序列的长度（实际上这里只要有解就行，不一定要最长）。因此，可以先对数组求和，然后看他是不是偶数，是的话才能继续往下做。然后这道题就变成0/1背包模板题了，物品个数为nums.size()，背包容量为sum / 2；物品i的容量为nums[i]，价值为1，要取最大的。

参考代码如下：

bool canPartition(vector<int>& nums) {
    int n = nums.size();
    int v = reduce(nums.begin(), nums.end(), 0);
    if (v % 2)
        return false;
    else
        v /= 2;

    // 0/1背包问题
    vector<int> dp(v + 5, -1919810);
    dp[0] = 0;
    for (int i = 0; i < n; ++i)
        for (int j = v; j >= nums[i]; --j)
            dp[j] = max(dp[j], dp[j - nums[i]] + 1);

    return dp[v] > 0;
}

494. 目标和 - 力扣（LeetCode）

可以发现，正数之和 + 负数绝对值之和 = 数组nums所有元素和，那么 负数绝对值之和 = 数组nums所有元素和 - 正数之和。去掉绝对值，负数之和 = 正数之和 - 数组nums所有元素和。我们最后要让正数之和 + 负数之和 = target，因此有正数之和 = (元素和 + target) / 2。

在正数之和存在的前提下，这道题就变成了经典01背包问题：容量为正数之和的背包中有nums.size()个物品，物品i的容积为nums[i]，价值为1，要取方案总数：

int findTargetSumWays(vector<int>& nums, int target) {
    int sum = reduce(nums.begin(), nums.end(), 0);
    if (sum + target < 0 || (target + sum) % 2)
        return 0;

    int n = nums.size();
    int v = (target + sum) / 2;
    vector<int> dp(v + 5, 0);
    // 初始化: 容量为0的背包有且只有一种解法(不放)
    dp[0] = 1;	

    for (int i = 0; i < n; ++i)
        for (int j = v; j >= nums[i]; --j)
            dp[j] += dp[j - nums[i]];

    return dp[v];
}

494. 目标和
2787. 将一个数字表示成幂的和的方案数 1818
474. 一和零（二维）
1049. 最后一块石头的重量 II 2092
1774. 最接近目标价格的甜点成本
879. 盈利计划 2204
3082. 求出所有子序列的能量和 ~2300
956. 最高的广告牌 2381
2518. 好分区的数目 2415
2742. 给墙壁刷油漆 2425
LCP 47. 入场安检
2291. 最大股票收益（会员题）
2431. 最大限度地提高购买水果的口味（会员题）

完全背包

322. 零钱兑换 - 力扣（LeetCode）

是完全背包模板题，背包容量为amount，有coins.size()种物品，第i种物品库存无限，容量为coins[i]，价值为1。我们要求装满背包后总价值最小。

int coinChange(vector<int>& coins, int amount) {
    int n = coins.size();
    int v = amount;

    vector<int> dp(v + 5, 114514);
    dp[0] = 0;
    for (int i = 0; i < n; ++i)
        for (int j = coins[i]; j <= v; ++j)
            dp[j] = min(dp[j], dp[j - coins[i]] + 1);

    return dp[v] == 114514 ? -1 : dp[v];
}

518. 零钱兑换 II - 力扣（LeetCode）

和上面的一样，就是改成了求方案数量：

int change(int amount, vector<int>& coins) {
    int n = coins.size();
    int v = amount;

    vector<int> dp(v + 5, 0);
    dp[0] = 1;
    for (int i = 0; i < n; ++i)
        for (int j = coins[i]; j <= v; ++j)
            dp[j] += dp[j - coins[i]];

    return dp[v];
}

物品可以重复选，无个数限制。

279. 完全平方数
1449. 数位成本和为目标值的最大数字 1927 打印方案

多重背包

2585. 获得分数的方法数 - 力扣（LeetCode）

const int MOD = 1e9 + 7;
int waysToReachTarget(int target, vector<vector<int>>& types) {
    // 多重背包问题
    // 由于同类型题目无法区分，导致不能用二进制优化
    // 且二进制优化适合求最值, 而不是求方案数

    int n = types.size();
    int m = target;
    vector<vector<int>> dp(n + 5, vector<int>(m + 5, 0));
    dp[0][0] = 1;

    for (int i = 1; i <= n; ++i)
        for (int j = 0; j <= m; ++j)
            for (int k = 0; k <= types[i - 1][0] && k * types[i - 1][1] <= j; ++k)
                dp[i][j] = (dp[i][j] + dp[i - 1][j - k * types[i - 1][1]]) % MOD;

    return dp[n][m];
}

尝试一维优化：

const int MOD = 1e9 + 7;
int waysToReachTarget(int target, vector<vector<int>>& types) {
    // 多重背包问题
    // 由于同类型题目无法区分，导致不能用二进制优化
    // 且二进制优化适合求最值, 而不是求方案数

    int n = types.size();
    int m = target;
    vector<int> dp(m + 5, 0);
    dp[0] = 1;

    for (int i = 0; i < n; ++i)
        for (int j = target; j >= types[i][1]; --j)
            for (int k = 1; k <= types[i][0] && k * types[i][1] <= j; ++k)
                dp[j] = (dp[j] + dp[j - k * types[i][1]]) % MOD;

    return dp[m];
}

物品可以重复选，有个数限制。

2902. 和带限制的子多重集合的数目 2759

分组背包

1155. 掷骰子等于目标和的方法数 - 力扣（LeetCode）

朴素版分组背包如下：

const int MOD = 1e9 + 7;
int numRollsToTarget(int n, int k, int target) {
    // 分组背包问题
    vector<vector<int>> dp(n + 5, vector<int>(target + 5, 0));
    dp[0][0] = 1;

    for (int i = 1; i <= n; ++i)
        for (int j = 0; j <= target; ++j)
            for (int x = 1; x <= k; ++x)
                if (x <= j)
                    dp[i][j] = (dp[i][j] + dp[i - 1][j - x]) % MOD;

    return dp[n][target];
}

``` 同一组内的物品至多/恰好选一个。

掷骰子等于目标和的方法数 1654
最小化目标值与所选元素的差 2010
从栈中取出 K 个硬币的最大面值和 2158