思想

DFS算法，也称回溯算法，本质上就是一种暴力穷举算法。解决一个回溯问题，实际上就是一个决策树的遍历过程，站在决策树的一个节点上，只需要思考以下三个问题：

1. 路径：已经做出的选择；
2. 选择列表：当前可做出的选择；
3. 结束条件：已经到达决策树底层，无法再做出选择。

DFS算法的代码框架如下：

result = []
def dfs(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return
    
    for 选择 in 选择列表:
        做出选择
        dfs(路径, 选择列表)
        撤销选择

其核心就是for循环里的递归，在递归调用前“做出选择”，在递归调用后“撤销选择”。

全排列问题

46. 全排列 - 力扣（LeetCode）

决策树

首先，画出该问题的决策树。例如求[1, 2, 3]全排列的决策树如下：

那么就可以确定路径、选择列表和结束条件了：

• 路径：已经选择了的数字
• 选择列表：还可以做出选择的数字
• 结束条件：到达决策树底部，选择列表为空

写DFS代码

参考代码如下：

vector<vector<int>> paths;

void dfs(vector<int>& nums, vector<int>& path, vector<int>& used)
{
    // 结束条件
    if (nums.size() == path.size())
    {
        paths.push_back(path);
        return;
    }

    for (int i = 0; i < nums.size(); ++i)
    {
        if (!used[i])
        {
            // 做出选择
            path.push_back(nums[i]);
            used[i] = 1;
            // dfs
            dfs(nums, path, used);
            // 撤销选择
            path.pop_back();
            used[i] = 0;
        }
    }
}

vector<vector<int>> permute(vector<int>& nums) {
    vector<int> path, used(nums.size(), 0);
    dfs(nums, path, used);
    return paths;
}

这里没有显式记录“选择列表”，而是使用used[i]记录nums[i]是否已被选择过。

N皇后问题

51. N 皇后 - 力扣（LeetCode）

52. N 皇后 II - 力扣（LeetCode）

思路一

可以按行枚举，枚举每一行皇后可以放到哪儿。然后边做边判断，该路径放的皇后有无冲突，有的话可以直接停止DFS，往回走。这里就用到了 剪枝 的思想，如果当前判断发现DFS没用了，则不必继续DFS，直接返回原来的状态。

画决策树

思路一的决策树如下：

写DFS代码

参考代码如下：

// 所有答案
vector<vector<string>> paths;
// 当前答案
vector<string> path;
// 皇后在列, 副对角线, 主对角线是否能放
vector<int> col, dg, udg;

void dfs(int u, int n)
{
    // 结束条件
    if (u == n)
    {
        paths.push_back(path);
        return;
    }

    for (int i = 0; i < n; ++i)
    {
        // 检查皇后是否能放
        if (!col[i] && !dg[u + i] && !udg[n - u + i])
        {
            // 做出选择
            path[u][i] = 'Q';
            col[i] = dg[u + i] = udg[n - u + i] = 1;

            dfs(u + 1, n);

            // 撤销选择
            path[u][i] = '.';
            col[i] = dg[u + i] = udg[n - u + i] = 0;
        }
    }
}

vector<vector<string>> solveNQueens(int n) {
    // 初始化
    col.resize(20, 0);
    dg.resize(20, 0);
    udg.resize(20, 0);
    path.resize(n, string(n, '.'));

    dfs(0, n);

    return paths;
}

这里用3个数组存储皇后是否能在列和两个对角线上存放的状态。有关这三个数组的位置关系推导如下：

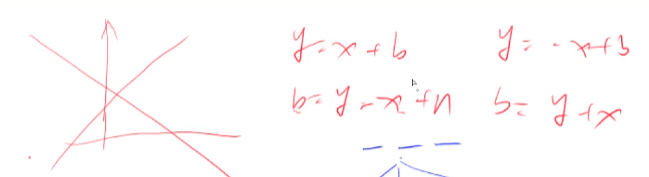
如图所示，对于在棋盘(x, y)上的棋子，可以将它抽象为两个直线的交点，而对于棋盘上的每一个位置，这两个直线也是不一样的。因此可以用每组直线的截距去表示一个位置在列、两个对角线上存放的状态。

思路二

除了按行枚举外，还可以按棋盘上的每个格子枚举，分为在该格子上放/不放两种状态。

画决策树

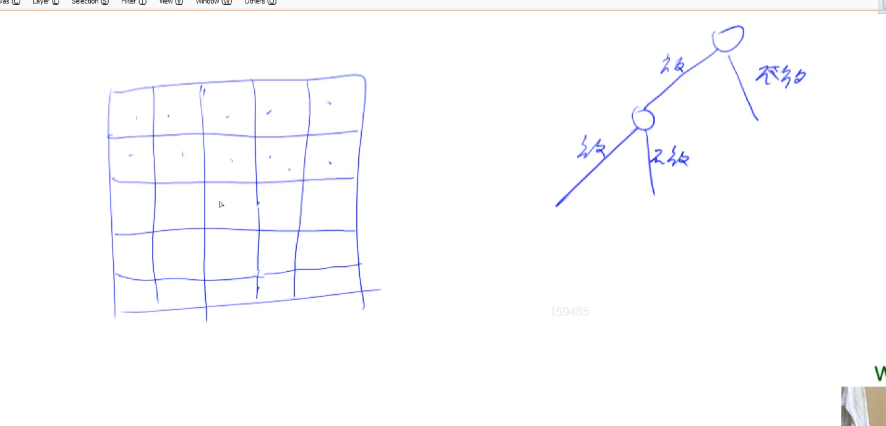
写DFS代码

// 所有答案
vector<vector<string>> paths;
// 当前答案
vector<string> path;
// 皇后在行,列, 副对角线, 主对角线是否能放
vector<int> row, col, dg, udg;

void dfs(int x, int y, int u, int n)
{
    // 每行走到最后一列, 变到下一行第一列
    if (y == n)
    {
        ++x;
        y = 0;
    }

    // 结束条件: 到最后一行, 放了n个皇后
    if (x == n)
    {
        if (u == n)
        {
            paths.push_back(path);
        }
        return;
    }

    // 做出不放皇后的选择, 不必撤销
    dfs(x, y + 1, u, n);
    if (!row[x] && !col[y] && !dg[x + y] && !udg[n + x - y])
    {
        // 做出放皇后的选择
        path[x][y] = 'Q';
        row[x] = col[y] = dg[x + y] = udg[n + x - y] = 1;

        dfs(x, y + 1, u + 1, n);

        // 撤销选择
        path[x][y] = '.';
        row[x] = col[y] = dg[x + y] = udg[n + x - y] = 0;
    }
}

vector<vector<string>> solveNQueens(int n) {
    // 初始化
    row.resize(20, 0);
    col.resize(20, 0);
    dg.resize(20, 0);
    udg.resize(20, 0);
    path.resize(n, string(n, '.'));

    dfs(0, 0, 0, n);

    return paths;
}

总结

回溯算法就是一个多叉树的遍历问题，关键就是在前序遍历和后序遍历的位置做一些操作。

参考资料

• 《labuladong的算法笔记》
• 算法基础课 - AcWing