思想

把一些问题抽象成图，从一个点开始，向四周扩散，然后问你求最短路。当边权为1时，才能用BFS。BFS找到的路径一定是最短的，但代价就是空间复杂度可能比DFS大得多。

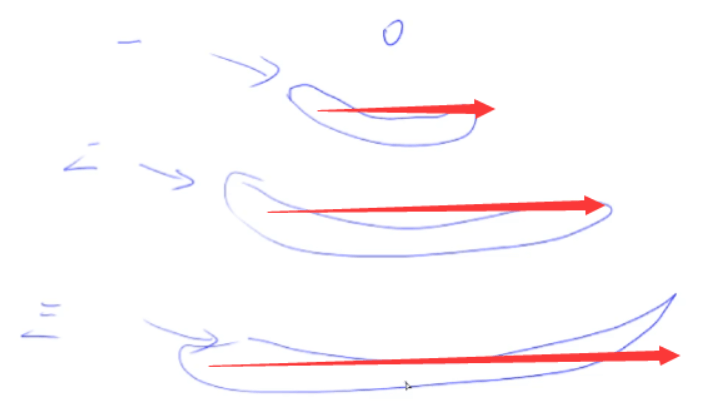
BFS的代码框架如下：

queue.push(初始状态)
while (队列不空)
{
	取队头t
    拓展队头t
}

练习题

最短路问题

走迷宫

844. 走迷宫 - AcWing题库

可以从起点(0, 0)开始BFS，每往前走一步，就记录当前位置离起点的距离。这样BFS结束后，终点(n - 1, m - 1)的距离就是离起点的最短距离。

参考代码如下：

#include <iostream>
#include <vector>
#include <queue>
using namespace std;

int n, m;
vector<vector<int>> map(110, vector<int>(110, 0)), dist(110, vector<int>(110, -1));

int bfs()
{
    // 初始状态
    queue<pair<int, int>> q;
    q.push({0, 0});
    dist[0][0] = 0;
    
    vector<pair<int, int>> dir = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
    // while队列不空
    while (!q.empty())
    {
        // 取队头
        auto [x, y] = q.front();
        q.pop();
        
        // 拓展队头
        for (int i = 0; i < 4; ++i)
        {
            auto [dX, dY] = dir[i];
            pair<int, int> next = {x + dX, y + dY};
            
            if (next.first >= 0 && next.first < n && 
                next.second >= 0 && next.second < m && 
                map[next.first][next.second] == 0 && 
                dist[next.first][next.second] == -1)
            {
                dist[next.first][next.second] = dist[x][y] + 1;
                q.push(next);
            }
        }
    }
    
    return dist[n - 1][m - 1];
}

int main()
{
    cin >> n >> m;
    for (int i = 0; i < n; ++i)
    {
        for (int j = 0; j < m; ++j)
        {
            cin >> map[i][j];
        }
    }
    
    cout << bfs() << '\n';
}

二叉树的最小深度

111. 二叉树的最小深度 - 力扣（LeetCode）

和“最短路径”有关，可以用BFS。最开始将根节点和它的深度1入队，然后开始BFS循环，取队头元素，判断是否是叶子节点（左右子节点均为空），不是的话就入队子节点和它的深度。

参考代码如下：

int minDepth(TreeNode* root) {
    if (root == nullptr)    return 0;

    queue<pair<TreeNode*, int>> q;
    q.push({root, 1});

    while (!q.empty())
    {
        // 取队头
        auto [cur, depth] = q.front();
        q.pop();

        // 验证是否是叶子节点
        if (cur->left == nullptr && cur->right == nullptr)
            return depth;

        // 拓展队头
        if (cur->left)  q.push({cur->left, depth + 1});
        if (cur->right) q.push({cur->right, depth + 1});
    }

    return 1;
}

打开转盘锁

752. 打开转盘锁 - 力扣（LeetCode）

要求打开转盘锁的最小次数，可用BFS来解决，首先看看如何根据问题构造要层序遍历的多叉树：

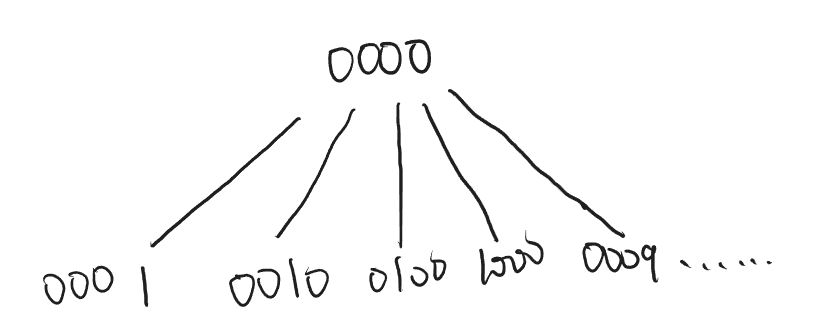
锁的每个状态可作为多叉树的节点，每次上/下拨视为状态转移。接下来，我们先把工具函数准备好：

// 将转盘锁从左往右第i为下拨
string plus(string str, int i)
{
    if (str[i] == '9')
        str[i] = '0';
    else
        ++str[i];
    return str;
}

string minus(string str, int i)
{
    if (str[i] == '0')
        str[i] = '9';
    else
        --str[i];
    return str;
}

然后就能写BFS框架了，需要注意的是，如果转出deadends里的数字，需要跳过本轮BFS。参考代码如下：

string plus(string str, int i)
{
    if (str[i] == '9')
        str[i] = '0';
    else
        ++str[i];
    return str;
}

string minus(string str, int i)
{
    if (str[i] == '0')
        str[i] = '9';
    else
        --str[i];
    return str;
}

int openLock(vector<string>& deadends, string target) {
    // 使用Hash存储deadends, 进行O(1)查询节省时间
    unordered_set<string> visited;
    visited.insert(deadends.begin(), deadends.end());

    // 直接得出答案的情况
    if (visited.count(target))  return -1;
    if (target == "0000")    return 0;

    // BFS
    queue<pair<string, int>> q;
    q.push({"0000", 0});

    while (!q.empty())
    {
        // 取队头
        auto [cur, ans] = q.front();
        q.pop();

        // 验证是否是答案
        if (cur == target)
            return ans;
        // 转到deadend里的数字就放弃BFS
        if (visited.count(cur))
            continue;

        // 拓展队头
        visited.insert(cur);
        for (int i = 0; i < 4; ++i)
        {
            string tmp = plus(cur, i);
            if (!visited.count(tmp))
                q.push({tmp, ans + 1});

            tmp = minus(cur, i);
            if (!visited.count(tmp))
                q.push({tmp, ans + 1});
        }
    }

    return -1;
}

八数码

845. 八数码 - AcWing题库

和上面的的开锁问题同理，但这里有个难点，就是如何用一行字符串存储3x3棋盘：

• 首先找到目标字符在字符串中的索引。
• 在3x3棋盘中，x = 索引 / 3，y = 索引 % 3
• 索引 = x * 3 + y

参考代码如下：

#include <iostream>
#include <vector>
#include <queue>
#include <unordered_map>
using namespace std;

string start = "", target = "12345678x";
unordered_map<string, int> dist;
queue<string> q;
vector<pair<int, int>> dir = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};

int main()
{
    char ch;
    while (cin >> ch)
        start += ch;
        
    // BFS
    q.push(start);
    dist[start] = 0;
    
    while (!q.empty())
    {
        string cur = q.front();
        q.pop();
        int dis = dist[cur];
        
        if (cur == target)
        {
            cout << dis;
            return 0;
        }
        
        // 拓展队头: 让x上下左右四个方向分别与x交换
        int idx = cur.find('x');
        int x = idx / 3, y = idx % 3;
        for (int i = 0; i < 4; ++i)
        {
            auto [dx, dy] = dir[i];
            int a = x + dx, b = y + dy;
            if (a >= 0 && a < 3 && b >= 0 && b < 3)
            {
                swap(cur[idx], cur[a * 3 + b]);
                if (!dist.count(cur))
                {
                    dist[cur] = dis + 1;
                    q.push(cur);
                }
                swap(cur[idx], cur[a * 3 + b]);
            }
        }
    }
    
    cout << -1;
}

其他

填充每个节点的下一个右侧节点指针

116. 填充每个节点的下一个右侧节点指针 - 力扣（LeetCode）

117. 填充每个节点的下一个右侧节点指针 II - 力扣（LeetCode）

是一道经典的二叉树的层序遍历题，应使用BFS。每次通过层序遍历，就能得到一层的二叉树节点，我们只需在用当层节点拓展下层节点的同时，将当层节点用链表连接起来就好了。

参考代码如下：

Node* connect(Node* root) {
    if (root == nullptr)
        return nullptr;

    vector<Node*> curLevel;
    curLevel.push_back(root);
    while (!curLevel.empty())
    {
        // 拓展下层所有节点的同时, 将当层节点连起来
        vector<Node*> nextLevel;
        for (int i = 0; i < curLevel.size(); ++i)
        {
            // 连接当层节点
            if (i)  
                curLevel[i - 1]->next = curLevel[i]; 

            // 拓展下层节点
            if (curLevel[i]->left) 
                nextLevel.push_back(curLevel[i]->left);  
            if (curLevel[i]->right) 
                nextLevel.push_back(curLevel[i]->right);  
        }
        curLevel = nextLevel;
    }

    return root;
}

参考资料

• 《labuladong的算法笔记》
• 算法基础课 - AcWing