并查集(Disjoint Set)结构，也称为Union-Find算法，主要是为了解决图论中 ”动态连通性“ 而存在的。

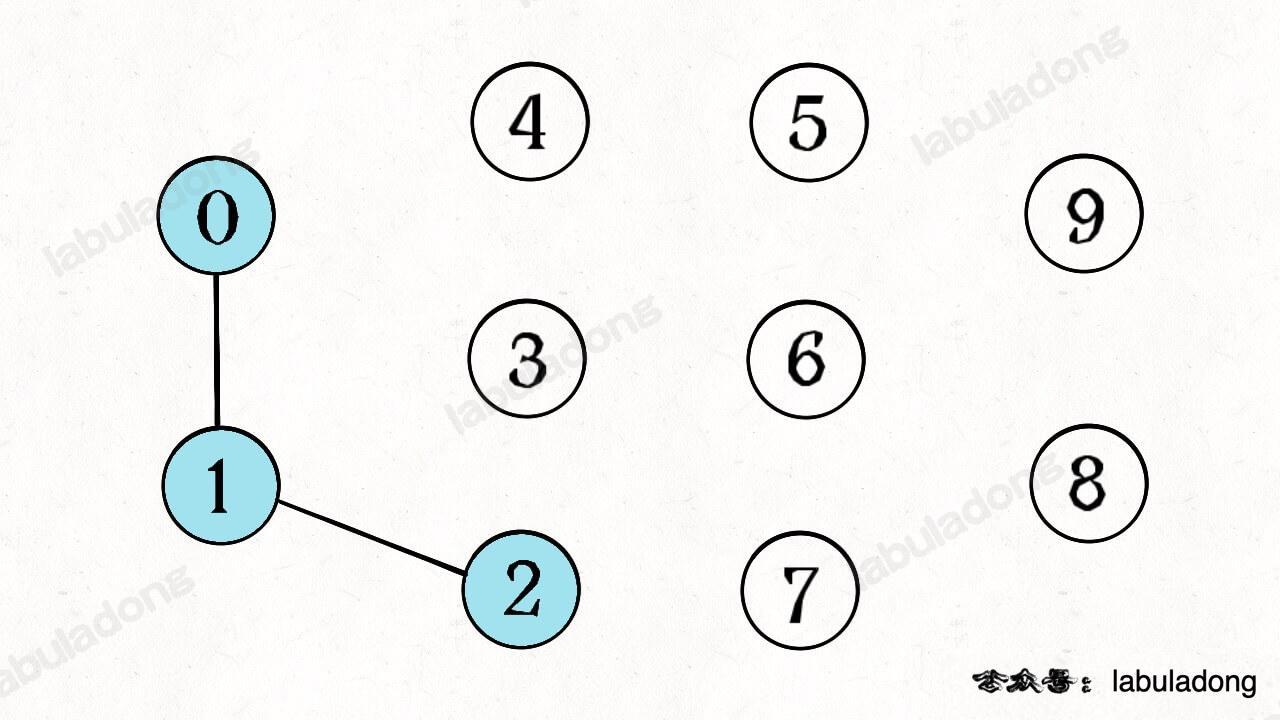
如图，上面有8个集合：[0, 1, 2], [3], ...，并查集可快速地用来处理以下问题：

• 将两个集合合并(union(a, b))
• 询问两个元素是否在同一个集合中（find(a, b)）

此外，图论中的部分DFS问题也可通过并查集来解决。

基本操作

初始化

我们用森林表示并查集，用数组来具体体现这个森林。在最开始，我们让所有节点的父节点都是它本身，这样就完成了并查集的初始化工作：

struct UF
{
    // 连通分量的数量
    int count;
    // 记录节点x的父节点parent[x]
    vector<int> parent;
    
    UF(int n)
        : count(n), parent(n)
    {
        // 刚开始所有节点的父节点都是自己
		for (int i = 0; i < n; ++i)
            parent[i] = i;
    }
};

合并两个集合

要想合并两个集合，只需让其中一个集合的根节点连接到另一个节点的根节点上即可：

void connect(int p, int q)
{
    int rootP = find(p);
    int rootQ = find(q);
    if (rootP == rootQ)
        return;
    // 合并操作
    parent[rootP] = rootQ;
    count--;
}

int find(int x)
{
    while (parent[x] != x)
        x = parent[x];
    return x;
}

接下来看看connect()和find()的时间复杂度。发现find()影响时间复杂度，它的功能是从某节点往上遍历到树根，最坏情况下树是一个链表，时间复杂度为，需要对它进行 路径压缩。

如图，想法让树变成这样的结构，时间复杂度就降到了：

路径压缩优化后的写法如下：

int find(int x)
{
    if (parent[x] != x)
        parent[x] = find(parent[x]);
    return parent[x];
}

判断两元素是否在一个集合中

只需判断两元素的根节点是否相同即可：

bool isConnected(int p, int q)
{
    int rootP = find(p);
    int rootQ = find(q);
    return rootP == rootQ;
}

综合起来，得到并查集数据结构：

struct UF
{
    // 连通分量的数量
    int count;
    // 记录节点x的父节点parent[x]
    vector<int> parent;
    
    void connect(int p, int q)
    {
        if (find(p) == find(q))
            return;
        
        parent[rootQ] = rootP;
        count--;
    }
    
    bool isConnected(int p, int q)
    {
        return find(p) == find(q);
    }
    
    int find(int x)
    {
        if (parent[x] != x)
            parent[x] = find(parent[x]);
        return parent[x];
    }
    
    UF(int n)
        : count(n), parent(n)
    {
        // 刚开始所有节点的父节点都是自己
		for (int i = 0; i < n; ++i)
            parent[i] = i;
        // 也能用<numeric>中的iota()
        // 为容器顺序分配 0, 1, 2, ...
        // iota(parent.begin(), parent.end(), 0);
    }
};

如果觉得写一个类太麻烦，也能只写一个find(x)，然后单独维护parent数组。

进阶操作

反向并查集

由于并查集仅支持插入关系而不能删除已有的关系，因此要进行“删除”的话得反向思考。先遍历所有关系和事件，提取出所有事件结果后仍保持的关系，将它们加入并查集中。然后逆序遍历事件，正序时遇到的“删除”事件相当于逆序下的“添加”，因此碰到删除时进行添加操作即可。

以美团240309春招实习笔试——小美的朋友关系（反向并查集）为例。

#include <iostream>
#include <map>
#include <set>
#include <stack>
#include <string>
#include <vector>
#include <algorithm>
using namespace std;

struct UF
{
    // 题给范围n太大, 用map存储
    map<int, int> pa;

    int find(int a)
    {
        if (pa[a] != a)
            pa[a] = find(pa[a]);
        return pa[a];
    }

    bool isConnect(int a, int b)
    {
        return find(a) == find(b);
    }

    void add(int x, int y)
    {
        pa[find(x)] = find(y);
    }
};

int main() {
    int n, m, q;
    cin >> n >> m >> q;

    // 存储关系
    UF uf;
    set<pair<int, int>> relations;
    while (m --)
    {
        int a, b;
        cin >> a >> b;

        // 初始化
        uf.pa[a] = a;
        uf.pa[b] = b;

        if (a > b)
            swap(a, b);
        relations.insert({a, b});
    }

    // 存储事件并维护关系
    vector<vector<int>> acts;
    while (q --)
    {
        int op, a, b;
        cin >> op >> a >> b;

        // 初始化
        uf.pa[a] = a;
        uf.pa[b] = b;

        if (a > b)
            swap(a, b);      
        // 删除操作, 合法就删除, 不合法就跳过
        if (op == 1)
        {
            if (relations.find({a, b}) != relations.end())
                relations.erase({a, b});
            else
                continue;
        }

        vector<int> tmp = {op, a, b};
        acts.emplace_back(tmp);
    }

    // 用剩余的关系建立并查集
    for (auto& [a, b] : relations)
        uf.add(a, b);
    
    // 逆向遍历事件
    reverse(acts.begin(), acts.end());
    stack<string> ans;
    for (auto& act : acts)
    {
        int op = act[0], a = act[1], b = act[2];
        if (op == 1)
            uf.add(a, b);
        else
        {
            if (uf.isConnect(a, b))
                ans.push("Yes");
            else
                ans.push("No");
        }
    }

    // 输出答案
    while (!ans.empty())
    {
        cout << ans.top() << '\n';
        ans.pop();
    }
}

练习题

Acwing

836. 合并集合 - AcWing题库

并查集模板题：

#include <iostream>
#include <vector>
using namespace std;

struct UF
{
    int count;
    vector<int> parent;
    
    UF(int n)
        : count(n), parent(n + 5)
    {
        for (int i = 0; i < n + 5; ++i)
            parent[i] = i;
    }
    
    int find(int x)
    {
        if (parent[x] != x)
            parent[x] = find(parent[x]);
        return parent[x];
    }
    
    void connect(int p, int q)
    {
        int rootP = find(p);
        int rootQ = find(q);
        if (rootP == rootQ)
            return;
        
        parent[rootQ] = rootP;
        count--;
    }
    
    bool isConnect(int p, int q)
    {
        return find(p) == find(q);
    }
};

int main()
{
    int n, m;
    cin >> n >> m;
    
    UF uf(n);
    
    char ch;
    int a, b;
    for (int i = 0; i < m; ++i)
    {
        cin >> ch >> a >> b;
        if (ch == 'M')
            uf.connect(a, b);
        else
        {
            if (uf.isConnect(a, b))
                cout << "Yes\n";
            else
                cout << "No\n";
        }
    }
}

837. 连通块中点的数量 - AcWing题库

除了可以在图中进行DFS，这道题也能用并查集来做，我们需要额外数组size来记录每个根节点所在连通块的点的数量。

#include <iostream>
#include <vector>
#include <string>
using namespace std;

struct UF
{
    // 连通分量的数量
    int count;
    // 记录节点x的父节点parent[x]
    vector<int> parent;
    // 记录各集合的连通块数量
    vector<int> size;
    
    void connect(int p, int q)
    {
        int rootP = find(p);
        int rootQ = find(q);
        if (rootP == rootQ)
            return;
        
        parent[rootQ] = rootP;
        size[rootP] += size[rootQ];
        count--;
    }
    
    bool isConnected(int p, int q)
    {
        return find(p) == find(q);
    }
    
    int find(int x)
    {
        if (parent[x] != x)
            parent[x] = find(parent[x]);
        return parent[x];
    }
    
    int getSize(int x)
    {
        return size[find(x)];
    }
    
    UF(int n)
        : count(n), parent(n + 5), size(n + 5, 1)
    {
        // 刚开始所有节点的父节点都是自己
		for (int i = 0; i < n + 5; ++i)
            parent[i] = i;
    }
};

int main()
{
    int n, m;
    cin >> n >> m;
    
    UF uf(n);
    
    int a, b;
    string q;
    for (int i = 0; i < m; ++i)
    {
        cin >> q;
        if (q == "C")
        {
            cin >> a >> b;
            uf.connect(a, b);
        }
        else if (q == "Q1")
        {
            cin >> a >> b;
            if (uf.isConnected(a, b))
                cout << "Yes\n";
            else
                cout << "No\n";
        }
        else
        {
            cin >> a;
            cout << uf.getSize(a) << '\n';
        }
    }
}

4493. 环形连通分量 - AcWing题库

从示例中可以发现，符合条件的环形连通分量，每个节点的度均为2。因此，我们可以使用并查集维护每个连通分量，顺便维护每个节点的度，如果度不为2，那就标记该集合不符合条件。

代码如下：

#include <iostream>
#include <vector>
#include <numeric>
using namespace std;

struct UF
{
    vector<int> parent, degree, valid;

    UF(int n)
        : parent(n + 5), degree(n + 5, 0), valid(n + 5, 1)
    {
        iota(parent.begin(), parent.end(), 0);
    }

    int find(int x)
    {
        return parent[x] == x ? parent[x] : parent[x] = find(parent[x]);
    }

    void connect(int p, int q)
    {
        parent[find(q)] = parent[find(p)];
        ++degree[p], ++degree[q];
    }
};

int main()
{
    int n, m;
    cin >> n >> m;
    UF uf(n);

    for (int i = 0; i < m; ++i)
    {
        int u, v;
        cin >> u >> v;
        uf.connect(u, v);
    }

    // 遍历度数不为2的节点
    for (int i = 1; i <= n; ++i)
        if (uf.degree[i] != 2)
            uf.valid[uf.find(i)] = 0;

    // 记录答案
    int ans = 0;
    for (int i = 1; i <= n; ++i)
    {
        if (uf.valid[uf.find(i)] && i == uf.find(i))
            ++ans;
    }
        
    cout << ans;
}

LeetCode

分享丨【题单】常用数据结构（前缀和/差分/栈/队列/堆/字典树/并查集/树状数组/线段树） - 力扣（LeetCode）

基础

323. 无向图中连通分量的数目 - 力扣（LeetCode）

直接用UF类就行：

struct UF
{
    int count;
    vector<int> parent;

    UF(int n)
        : count(n), parent(n + 5)
        {
            for (int i = 0; i < parent.size(); ++i)
                parent[i] = i;
        }

    int find(int x)
    {
        if (parent[x] != x)
            parent[x] = find(parent[x]);
        return parent[x];
    }

    void connect(int p, int q)
    {
        if (find(p) == find(q))
            return;

        parent[find(q)] = find(p);
        count--;
    }
};
public:
int countComponents(int n, vector<vector<int>>& edges) {
    UF uf(n);
    for (auto& points : edges)
        uf.connect(points[0], points[1]);
    return uf.count;
}

130. 被围绕的区域 - 力扣（LeetCode）

可以用DFS来做，先用for循环遍历边界，使用DFS把和边界相连的O变成#；然后再遍历整个棋盘，把剩下的O变成X，把#变成O。

也能用并查集来做，我们将位于边界的O加入根节点为dummy的集合，然后将内部的O加入到旁边的O的集合，最后将不属于dummy集合的O变成X就好了。参考代码如下：

class Solution {
    struct UF
    {
        vector<int> pa;

        int find(int x)
        {
            if (pa[x] != x)
                pa[x] = find(pa[x]);
            return pa[x];
        }

        void add(int a, int b)
        {
            pa[find(a)] = find(b);
        }

        bool isConnect(int a, int b)
        {
            return find(a) == find(b);
        }

        UF(int n) : pa(n + 5) 
        {
            iota(pa.begin(), pa.end(), 0);
        }
    };

    public:
    void solve(vector<vector<char>>& board) {
        int m = board.size(), n = board[0].size();
        UF uf(m * n + 5);

        // 边界O加入dummy
        for (int i = 0; i < m; ++i)
        {
            if (board[i][0] == 'O')
                uf.add(i * n, m * n);
            if (board[i][n - 1] == 'O')
                uf.add(i * n + n - 1, m * n);
        }
        for (int j = 0; j < n; ++j)
        {
            if (board[0][j] == 'O')
                uf.add(j, m * n);
            if (board[m - 1][j] == 'O')
                uf.add((m - 1) * n + j, m * n);
        }

        // 内部加入旁边的
        vector<pair<int, int>> dir = {{1, 0}, {0, 1}, {0, -1}, {-1, 0}};
        for (int i = 1; i < m - 1; ++i)
        {
            for (int j = 1; j < n - 1; ++j)
            {
                if (board[i][j] == 'O')
                {
                    for (auto& [dx, dy] : dir)
                    {
                        int x = i + dx, y = j + dy;
                        if (board[x][y] == 'O')
                            uf.add(x * n + y, i * n + j);
                    }
                }
            }
        }

        // 所有遍历一次
        for (int i = 1; i < m - 1; ++i)
        {
            for (int j = 1; j < n - 1; ++j)
            {
                if (!uf.isConnect(i * n + j, m * n))
                    board[i][j] = 'X';
            }
        }
    }
};

990. 等式方程的可满足性 - 力扣（LeetCode）

可以用并查集来做，用并查集维护26个字母的相等性。开始先遍历一遍equations，维护字母的相等关系；然后再次遍历，这时查看不等关系，如果应该不等却相等了，就是错的。

参考代码如下：

class Solution {
struct UF
{
    vector<int> pa;

    int find(int x)
    {
        if (pa[x] != x)
            pa[x] = find(pa[x]);
        return pa[x];
    }

    void connect(int a, int b)
    {
        pa[find(a)] = pa[find(b)];
    }

    bool isConnect(int a, int b)
    {
        return find(a) == find(b);
    }

    UF(int n) : pa(n + 5) 
    {
        iota(pa.begin(), pa.end(), 0);
    }
};

public:
    bool equationsPossible(vector<string>& equations) {
        UF uf(26);

        // 先获取相等关系
        for (auto& str : equations)
        {
            if (str.find("==") != string::npos)
                uf.connect(str[0] - 'a', str[3] - 'a');
        }

        // 再用不等关系判断正误
        for (auto& str : equations)
        {
            if (str.find("!=") != string::npos)
                if (uf.isConnect(str[0] - 'a', str[3] - 'a'))
                    return false;
        }

        return true;
    }
};

990. 账户合并
991. 句子相似性 II（会员题）
992. 彼此熟识的最早时间（会员题）
993. 近义词句子（会员题）

进阶

1202. 交换字符串中的元素 1855
1203. 按字典序排列最小的等效字符串
1204. 执行交换操作后的最小汉明距离 1892
1205. 情侣牵手 1999
1206. 移除最多的同行或同列石头 2035
1207. 相似字符串组 2054
1208. 你能穿过矩阵的最后一天 2124
1209. 处理含限制条件的好友请求 2131
1210. 保证图可完全遍历 2132
1211. 由斜杠划分区域 2136
1212. 找出最安全路径 2154
1213. 矩阵查询可获得的最大分数 2196
1214. 统计树中的合法路径数目 2428
1215. 好路径的数目 2445
1216. 字符串分组 2499
1217. 矩阵转换后的秩 2530
1218. 打砖块 2765
1219. 将子数组重新排序得到同一个二叉搜索树的方案数 思考：更快的做法 LCP 71. 集水器
1220. 最小化网格中的最大值（会员题）同 1632 题

公因数并查集

2709. 最大公约数遍历 2172
2710. 带阈值的图连通性 2221
2711. 按公因数计算最大组件大小 2272
2712. 数组的最大公因数排序 2429

数组并查集

1562. 查找大小为 M 的最新分组 1928
1563. 避免洪水泛滥 1974
1564. 删除操作后的最大子段和 2136
1565. 元素值大于变化阈值的子数组 2381

区间并查集

• 1851. 包含每个查询的最小区间 2286
• 2158. 每天绘制新区域的数量（会员题）

边权并查集

• 399. 除法求值
• 2307. 检查方程中的矛盾之处（会员题）