准备春招，算法题冲冲冲！

单调栈

单调栈即满足单调性的栈结构，分从小到大和从大到小两种。

例如，栈中自顶向下的元素为。插入元素时，为了保证单调性，得先弹出，然后才能插入。操作后栈变为。

为了让单调栈可用，应遵循 “及时去掉无用数据，保证栈中数据有序” 这一原则。

用数组模拟栈

除了可以用标准库的stack外，还能用数组简单模拟栈：

// 定义
const int N = 100010;
int stk[N], tt = 0;		// tt是栈顶

// 插入
stk[++tt] = x;

// 删除
tt--;

// 判断是否为空
if (tt > 0) 不空;
else		 空;

// 取栈顶元素
stk[tt];

例题

单调栈

830. 单调栈 - AcWing题库

这一题要保证栈顶元素始终是较小的数，如果栈顶数比当前数大，就让它出栈。

#include <iostream>
#include <stack>
#include <vector>
using namespace std;

int main()
{
    int n;
    cin >> n;
    
    vector<int> nums(n);
    for (int i = 0; i < n; ++i)
        cin >> nums.at(i);
        
    stack<int> stk;
    for (int i = 0; i < n; ++i)
    {
        while (!stk.empty() && stk.top() >= nums.at(i))
        {
            stk.pop();
        }
        
        if (!stk.empty())
        {
            cout << stk.top() << " ";
        }
        else
        {
            cout << "-1" << " ";
        }
        
        stk.push(nums.at(i));
    }
}

739. 每日温度 - 力扣（LeetCode）

这道题可以从右往左考虑，也能从左往右考虑。

首先看看从右往左的思路：

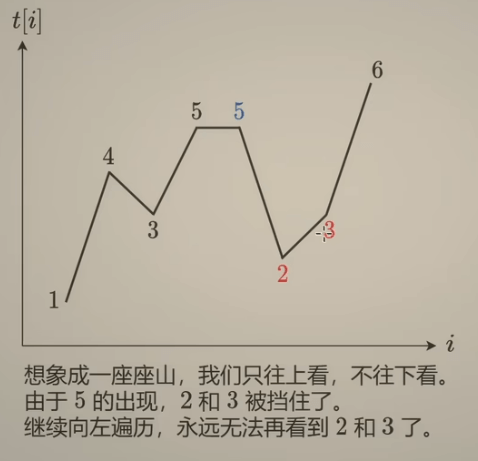
• 遍历到6，没有比6大的数，把6加入集合，答案为0
• 遍历到3，发现6比3大，把3加入集合，答案为1（6的下标 - 3的下标）
• 遍历到2，发现3比2大，把2加入集合，答案为1
• 遍历到5，发现6比5大，中间的2和3不要了，把5加入集合，答案为3
• 遍历到5，发现6比5大，中间的5不要了，。。。。。。

我们发现这个集合管理的数据刚好满足单调栈的特性（先进先出，单调性），可以用单调栈来做这道题。

vector<int> dailyTemperatures(vector<int>& temperatures) 
{
    vector<int> ans;
    ans.reserve(temperatures.size());

    // 从右往左, 单调栈
    stack<pair<int, int>> stk;
    for (int i = temperatures.size() - 1; i >= 0; --i)
    {
        while (!stk.empty() && stk.top().first <= temperatures.at(i))
        {
            stk.pop();
        }
        if (stk.empty())
        {
            stk.push({temperatures.at(i), i});
            ans.emplace_back(0);
        }
        else
        {
            ans.emplace_back(stk.top().second - i);
            stk.push({temperatures.at(i), i});
        }
    }

    reverse(ans.begin(), ans.end());
    return ans;
}

需要注意的是，由于我们是从右往左记录答案的，需要在最后一步把答案翻转过来。

然后是从左往右的思路：

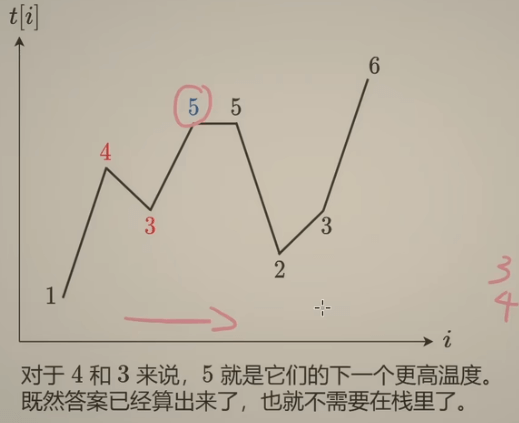
• 遍历1，1入栈
• 遍历4，发现栈顶1比4小，说明比1大的数是4，1出栈；4入栈
• 遍历3，3入栈
• 遍历5，发现栈顶3比5小，3出栈；发现栈顶4比5小，4出栈；5入栈
• ……

vector<int> dailyTemperatures(vector<int>& temperatures) {
    vector<int> ans(temperatures.size());

    // 存储下标
    stack<int> stk;
    for (int i = 0; i < temperatures.size(); ++i)
    {
        while (!stk.empty() && temperatures.at(stk.top()) < temperatures.at(i))
        {
            ans.at(stk.top()) = i - stk.top();
            stk.pop();
        }
        stk.push(i);
    }

    return ans;
}

42. 接雨水 - 力扣（LeetCode）

可以用单调栈来写，以示例1为例：

• 栈空，0入栈
• 由于1比0大，0出栈作为坑的中间，由于此时栈空，没有坑的左边，水会漏，因此放弃计算；1入栈
• 0比1小，0入栈
• 由于2比0大，0出栈作为坑的中间，此时栈中的1作为坑的左边不出栈（因为这个左边的1下次就会变成中间的1了），计算得出雨水为1；2入栈
• 1比2小，1入栈
• 0比1小，0入栈
• 由于1比0大，0出栈，此时左边1中间0右边1，计算水为1；1入栈
• 由于3比1大，1出栈，此时左边2中间1右边3，计算水为3（隔了3格宽）；3入栈
• 。。。。。。

代码如下：

int trap(vector<int>& height) {
    int ans = 0;
    stack<int> stk;
    for (int i = 0; i < height.size(); ++i)
    {
        while (!stk.empty() && height.at(i) >= height.at(stk.top()))
        {
            int midHeight = height.at(stk.top());
            int midPos = stk.top();
            stk.pop();
            if (stk.empty())
                break;
            // 不pop Left是因为要让它成为下一个mid
            int leftHeight = height.at(stk.top());
            int leftPos = stk.top();

            ans += (min(leftHeight, height.at(i)) - midHeight) * (i - leftPos - 1); 
        }

        stk.push(i);
    }

    return ans;
}

矩形系列

84. 柱状图中最大的矩形 - 力扣（LeetCode）

如图，我们可以发现最大矩形的高总是height[i]，那么剩下的就是求矩形宽的问题了。可以发现，最大矩形旁边总是有两个比它低的小矩形，那么问题就转换为如何找到这两个小矩形了。

可以用单调栈来找，比height[i]高的元素都出栈，最后栈顶元素就是旁边的矩形了，不过得要从左到右和从右到左找两次。最后遍历所有情况，取最大值即可。

参考代码如下：

int largestRectangleArea(vector<int>& heights) {
    int size = heights.size();
    // 找面积最大矩形左边的矩形
    stack<int> stk;
    vector<int> left(size, -1);     // 默认-1, 即第一个矩形的左边
    for (int i = 0; i < size; ++i)
    {
        // 让比最大矩形(假设为i)还大的矩形出栈
        while (!stk.empty() && heights.at(stk.top()) >= heights.at(i))
        {
            stk.pop();
        }
        // 如果栈内有结果, 栈顶就是左边的矩形
        if (!stk.empty())
        {
            left.at(i) = stk.top();
        }
        stk.push(i);
    }

    // 找面积最大矩形右边的矩形
    while (!stk.empty())
    {
        stk.pop();
    }
    vector<int> right(size, size);  // 默认size, 即最后一个矩形的右边
    for (int i = size - 1; i >= 0; --i)
    {
        while (!stk.empty() && heights.at(stk.top()) >= heights.at(i))
        {
            stk.pop();
        }
        if (!stk.empty())
        {
            right.at(i) = stk.top();
        }
        stk.push(i);
    }

    // 遍历所有情况, 找出最大值
    int ans = -1;
    for (int i = 0; i < size; ++i)
    {
        ans = max(ans, (right.at(i) - left.at(i) - 1) * heights.at(i));
    }

    return ans;
}

字典序最小

贡献法

参考资料

• 分享｜【题单】单调栈（矩形系列/字典序最小/贡献法） - 力扣（LeetCode）
• 算法基础课 - AcWing