1 - 二叉树

发表于 2024-04-24 更新于 2024-04-29 分类于 cpp ，数据结构与算法， 2-数据结构，树阅读次数： Waline：本文字数： 9.1k 阅读时长 ≈ 8 分钟

二叉树不仅仅是数组/链表这类基本数据结构和图这类高级数据结构中间的过滤，更代表着递归的思维模式，能够帮助我们更好地掌握计算机思维，得心应手地借助计算机解决问题。

一般问题

解题思路

二叉树解题的思维模式分为两类：

是否可以通过遍历一次二叉树得到答案？如果可以，用一个遍历函数和外部变量来实现。
是否可以定义一个递归函数，通过解决子问题（子树）的答案推导出原问题的答案？如果可以，写出递归函数的定义，充分利用函数返回值得到答案。

无论使用哪种思维模式，都需要思考：如果单独抽出一个二叉树节点，需要对它做什么事情？需要在什么时候（前/中/后序位置）做？。

练习题

翻转二叉树

226. 翻转二叉树 - 力扣（LeetCode）

只要把二叉树上每一节点的左右节点进行交换，最后的结果就是翻转后的二叉树。

首先看看能不能以 遍历一次二叉树 的方法解决，我们只需遍历每个节点，然后将其左右子节点进行交换即可。在什么位置交换？前序或者后序。

参考代码如下：

void traverse(TreeNode* root)
{
    if (root)
    {
        // =前序位置=
        swap(root->left, root->right);
        // =========
        traverse(root->left);
        // =中序位置=
        // =========
        traverse(root->right);
        // =后序位置=
        // =========
    }
}
TreeNode* invertTree(TreeNode* root) {
    traverse(root);
    return root;
}

然后看看能不能以递归的方法解决。首先给递归函数下定义：

// 将以root为根的二叉树翻转, 返回翻转后二叉树的根节点
TreeNode* invertTree(TreeNode* root);

对于某一个二叉树节点x，执行invertTree(x)时应该干什么？可以先用invertTree(x->left)翻转它的左子树，再用invertTree(x->right)翻转它的右子树。最后只剩下x->left和x->right两个节点未交换，交换他俩就好了。

参考代码如下：

TreeNode* invertTree(TreeNode* root) {
    if (root == nullptr)
        return nullptr;

    invertTree(root->left);
    invertTree(root->right);

    swap(root->left, root->right);

    return root;
}

将二叉树展开为链表

114. 二叉树展开为链表 - 力扣（LeetCode）

首先看看如何用遍历的方式去做，由于题中说展开后的链表应该与二叉树的先序遍历顺序相同，那么我们就用先序遍历来做：

TreeNode *dummy;
vector<TreeNode*> nodes;

void traverse(TreeNode* root)
{
    if (root)
    {
        nodes.push_back(root);
        traverse(root->left);
        traverse(root->right);
    }
}

void flatten(TreeNode* root) {
    dummy = new TreeNode(0);
    traverse(root);

    TreeNode *prev, *cur;
    for (int i = 1; i < nodes.size(); ++i)
    {
        prev = nodes[i - 1];
        cur = nodes[i];
        prev->left = nullptr;
        prev->right = cur;
    }
}

然后看看如何用递归的方式去做，首先给出递归函数的定义：

// 输入节点root, 返回以root为根节点的链表
void flatten(TreeNode* root);

接下来，对于一个节点x，可以执行以下流程：

用flatten(x->left)和flatten(x->right)拉平左右子树
将拉平的左子树作为新右子树
将旧右子树添加到新右子树末尾

参考代码如下：

void flatten(TreeNode* root) {
    if (root == nullptr)   
        return;

    // 1. 拉平左右子树
    flatten(root->left);
    flatten(root->right);

    // 2. 左子树作为新右子树
    TreeNode *left = root->left, *right = root->right;
    root->left = nullptr;
    root->right = left;

    // 3. 旧右子树添加到新右子树末尾
    TreeNode *tmp = root;
    while (tmp->right)
        tmp = tmp->right;
    tmp->right = right;
}

最后，题目还有进阶要求：使用的空间复杂度展开这棵树，这要求我们不能用上面的方法了。不过不要担心，只需改进一下递归方法，让它不递归就行了。

如图，使用三个指针：

cur指针指向当前遍历的根节点。
next指针指向cur左子树的根节点。
pre指针指向next树的最右子节点。

然后将cur指针的右子树放到pre->right后：

最后将左子树变成右子树，继续遍历即可：

参考代码如下：

void flatten(TreeNode* root) {
    if (root == nullptr)   
        return;

    TreeNode* cur = root;
    while (cur)
    {
        // 找cur左子树next
        if (cur->left)
        {
            TreeNode* next = cur->left;
            // 找next子树的最右节点
            TreeNode* pre = next;
            while (pre->right)
                pre = pre->right;

            // cur右子树接到pre后面
            pre->right = cur->right;
            // cur左子树变成右子树
            cur->left = nullptr;
            cur->right = next;
        }
        cur = cur->right;
    }
}

构造类问题

解题思路

二叉树构造类问题一般都是使用上面 递归分解问题 的思路：构造整棵树 = 根节点 + 构造左子树 + 构造右子树。

练习题

构造最大二叉树

654. 最大二叉树 - 力扣（LeetCode）

最大二叉树 可以用下面的算法从 nums 递归地构建:

创建一个根节点，其值为 nums 中的最大值。
递归地在最大值左边的 子数组前缀上 构建左子树。
递归地在最大值右边的 子数组后缀上 构建右子树。

代码如下：

// 在数组[left, right]中寻找最大值, 构建二叉树.
// 返回根节点
TreeNode* build(vector<int>& nums, int left, int right)
{
    if (left > right)   
        return nullptr;

    int maxVal = nums[left], idx = left;
    for (int i = left; i <= right; ++i)
    {
        if (maxVal < nums[i])
        {
            maxVal = nums[i];
            idx = i;
        }
    }

    TreeNode* root = new TreeNode(maxVal);
    root->left = build(nums, left, idx - 1);
    root->right = build(nums, idx + 1, right);

    return root;
}

TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
    return build(nums, 0, nums.size() - 1);
}

前序中序构建二叉树

105. 从前序与中序遍历序列构造二叉树 - 力扣（LeetCode）

首先，需要构建根节点，要用前序序列第一个值为根节点的特性。接下来如何构建左右子树是个难题。

来看看这两个序列：

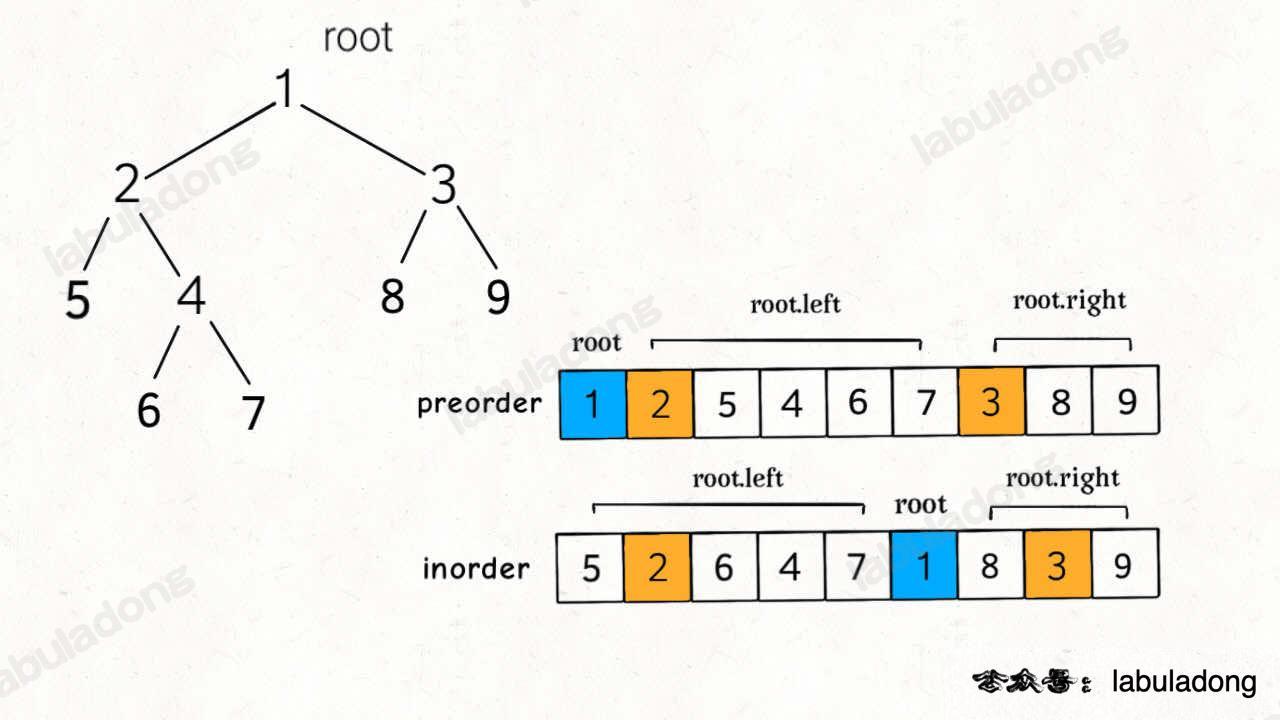
我们发现，在通过前序序列确定根节点后，可在中序序列中获得两个子树的节点。

给出递归构建二叉树的框架：

/**
*   在前序序列[preLeft, preRight]和中序序列[inLeft, inRight]中,
*   构建二叉树, 返回二叉树根结点
*/
TreeNode* build(vector<int>& preorder, int preLeft, int preRight,
                vector<int>& inorder, int inLeft, int inRight)
{
    if (preLeft > preRight || inLeft > inRight)
        return nullptr;

    // 前序序列找根节点, 然后确定它在中序序列的索引
    int rootVal = preorder[preLeft];
    int rootIdx = 0;
    for (int i = inLeft; i <= inRight; ++i)
        if (inorder[i] == rootVal)
            rootIdx = i;

    // 递归构建左右子树
    TreeNode* root = new TreeNode(rootVal);
    root->left = build(preorder, ?, ?, 
                       inorder, ?, ?);
    root->right = build(preorder, ?, ?, 
                        inorder, ?, ?);

    return root;
}

接下来就要确认递归创建左右子树中，两序列的范围怎么划分了。

首先是中序遍历，它比较好确定：

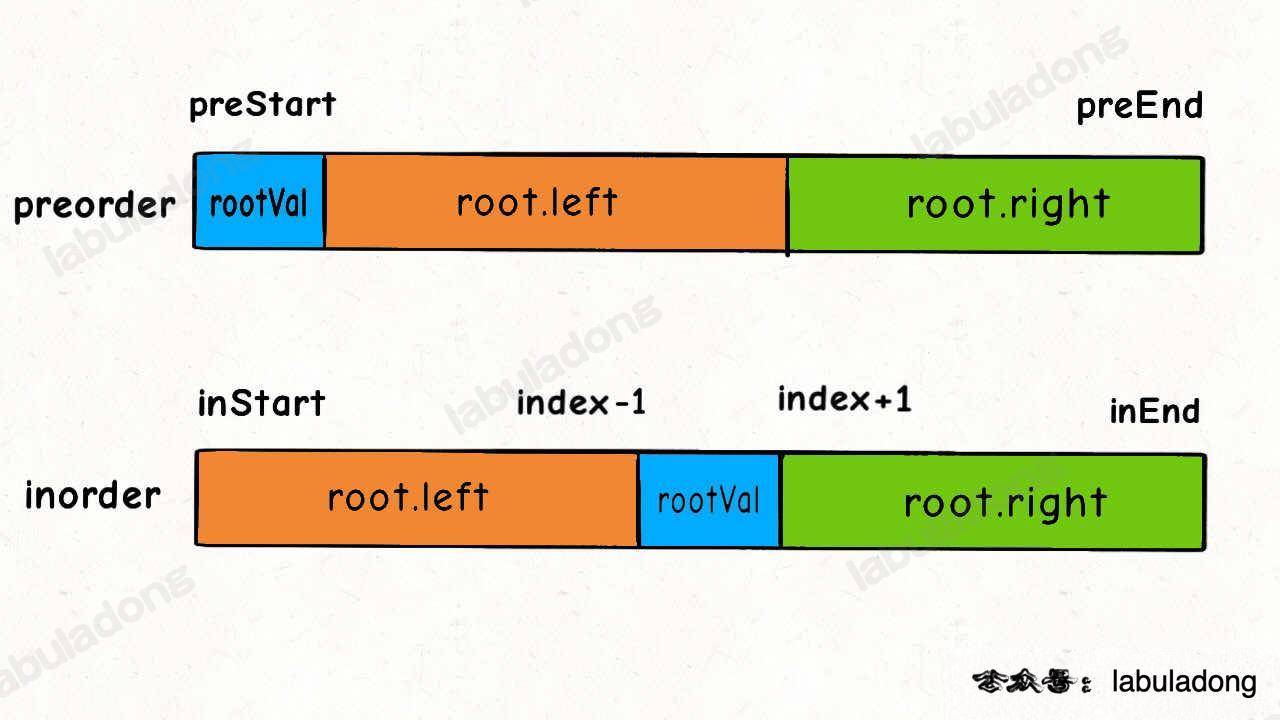
那么中序遍历的空就该填成：

root->left = build(preorder, ?, ?, 
                   inorder, inLeft, rootIdx - 1);
root->right = build(preorder, ?, ?, 
                    inorder, rootIdx + 1, inRight);

然后是先序遍历：

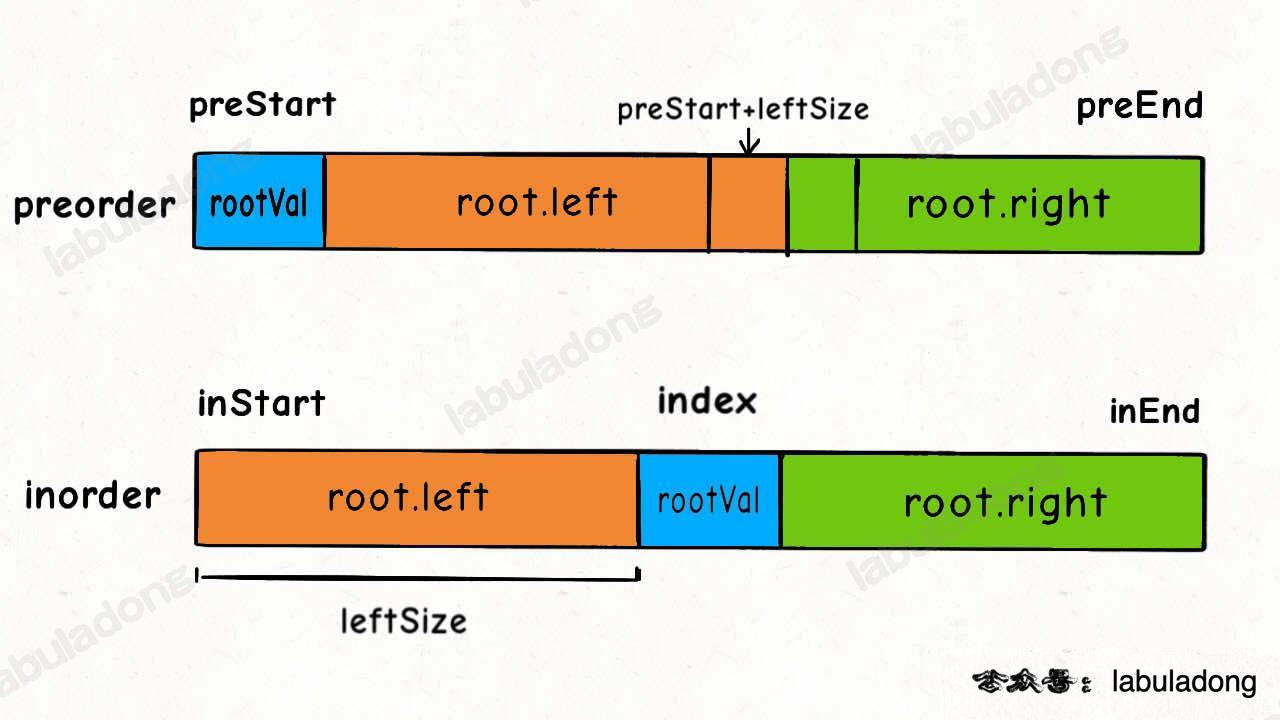
如图，可通过求出左子树节点数leftSize，进而求出左右子树的分界。那么先序遍历的空就该填成：

root->left = build(preorder, , ?, 
                   inorder, inLeft, rootIdx - 1);
root->right = build(preorder, ?, ?, 
                    inorder, rootIdx + 1, inRight);

参考代码如下：

TreeNode* build(vector<int>& preorder, int preLeft, int preRight,
                vector<int>& inorder, int inLeft, int inRight)
{
    if (preLeft > preRight || inLeft > inRight)
        return nullptr;

    // 前序序列找根节点, 然后确定它在中序序列的索引
    int rootVal = preorder[preLeft];
    int rootIdx = 0;
    for (int i = inLeft; i <= inRight; ++i)
        if (inorder[i] == rootVal)
            rootIdx = i;

    // 递归构建左右子树
    TreeNode* root = new TreeNode(rootVal);
    int leftSize = rootIdx - inLeft;
    root->left = build(preorder, preLeft + 1, preLeft + leftSize, 
                       inorder, inLeft, rootIdx - 1);
    root->right = build(preorder, preLeft + leftSize + 1, preRight, 
                        inorder, rootIdx + 1, inRight);

    return root;
}

TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
    return build(preorder, 0, preorder.size() - 1,
                 inorder, 0, inorder.size() - 1);
}

后序中序构建二叉树

106. 从中序与后序遍历序列构造二叉树 - 力扣（LeetCode）

和前序中序类似，后序和中序的关系图如下：

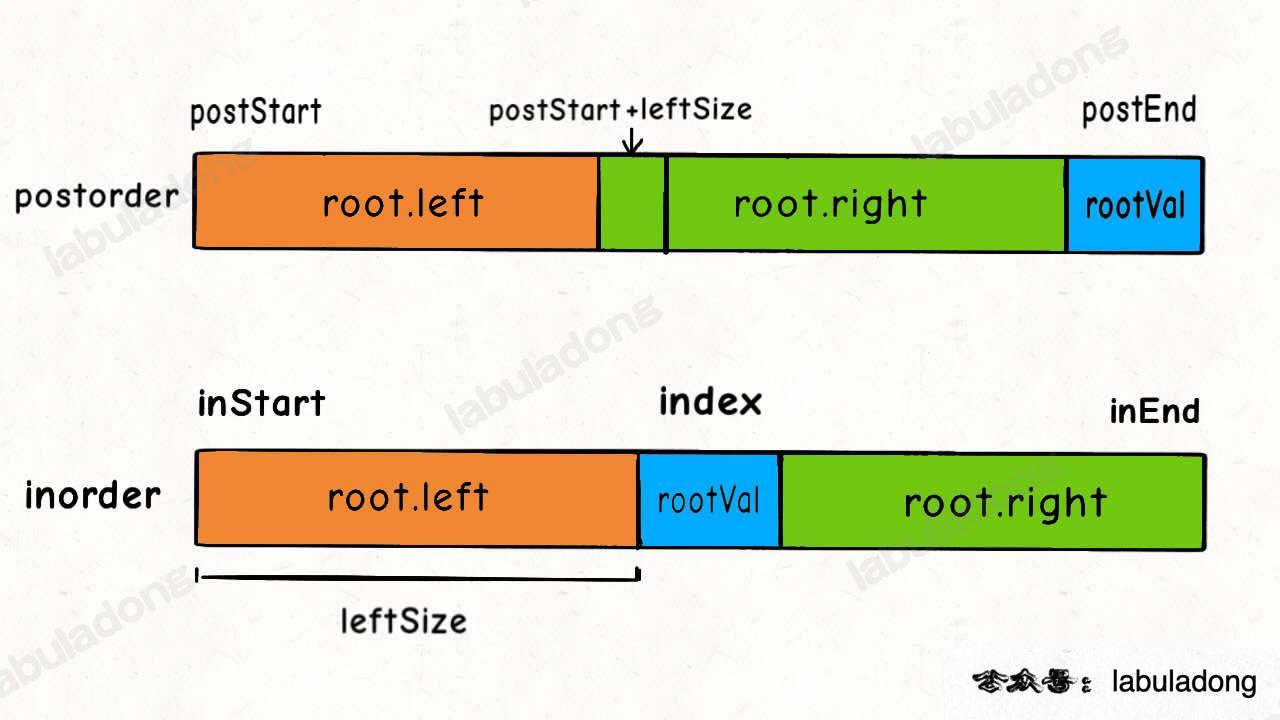
参考代码如下：

TreeNode* build(vector<int>& inorder, int inLeft, int inRight,
                vector<int>& postorder, int postLeft, int postRight)
{
    if (inLeft > inRight || postLeft > postRight)
        return nullptr;

    // 确认根节点
    int rootVal = postorder[postRight];
    int rootIdx = 0;
    for (int i = inLeft; i <= inRight; ++i)
        if (rootVal == inorder[i])
            rootIdx = i;

    // 构造左右子树
    TreeNode* root = new TreeNode(rootVal);
    int leftSize = rootIdx - inLeft;
    root->left = build(inorder, inLeft, rootIdx - 1,
                       postorder, postLeft, postLeft + leftSize - 1);
    root->right = build(inorder, rootIdx + 1, inRight,
                        postorder, postLeft + leftSize, postRight - 1);

    return root;
}

TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
    return build(inorder, 0, inorder.size() - 1,
                 postorder, 0, postorder.size() - 1);
}

前序后序构建二叉树

889. 根据前序和后序遍历构造二叉树 - 力扣（LeetCode）

只靠前序后序而没有中序构造的二叉树是不唯一的。因为在之前两道题中，我们靠前序/后序确认根节点位置，然后靠中序划分左右子树。现在没有中序了，也就不会划分左右子树了，因此，其中一种可能的构建方法如下：

把前序遍历的第一个元素作为根节点
把前序遍历的第二个元素作为左子树根节点
在后序遍历中寻找左子树根节点，确认左子树索引边界，然后确认右子树。

两个遍历的关系如下：

参考代码如下：

TreeNode* build(vector<int>& preorder, int preLeft, int preRight,
                vector<int>& postorder, int postLeft, int postRight)
{
    if (preLeft > preRight || postLeft > postRight)
        return nullptr;

    // 确认根节点
    if (preLeft == preRight)
        return new TreeNode(preorder[preLeft]);
    if (postLeft == postRight)
        return new TreeNode(postorder[postLeft]);
    int rootVal = preorder[preLeft];

    // 确认左子树根节点
    int leftRootVal = preorder[preLeft + 1];
    int leftRootIdx = 0;
    for (int i = postLeft; i <= postRight; ++i)
        if (leftRootVal == postorder[i])
            leftRootIdx = i;

    // 递归构建左右子树
    TreeNode* root = new TreeNode(rootVal);
    int leftSize = leftRootIdx - postLeft + 1;
    root->left = build(preorder, preLeft + 1, preLeft + leftSize,
                       postorder, postLeft, leftRootIdx);
    root->right = build(preorder, preLeft + leftSize + 1, preRight,
                        postorder, leftRootIdx + 1, postRight - 1);

    return root;
}

TreeNode* constructFromPrePost(vector<int>& preorder, vector<int>& postorder) {
    return build(preorder, 0, preorder.size() - 1,
                 postorder, 0, postorder.size() - 1);
}

序列化类问题

序列化与反序列化的目的就是 以某种特定格式组织数据，使得数据可以独立于编程语言。

解题思路

297. 二叉树的序列化与反序列化 - 力扣（LeetCode）

使用前中/中后序遍历

详见上面的构造类问题。

使用带空指针信息的前/后序遍历

以前序遍历为例，首先通过前序遍历得到序列化信息：

void traverse(TreeNode* root, string& data)
{
    if (root)
    {
        data += to_string(root->val) + ",";
        traverse(root->left, data);
        traverse(root->right, data);
    }
    else
        data += "#,";
}

string serialize(TreeNode* root) {
    string data = "";
    traverse(root, data);
    return data;
}

然后根据序列化信息去建树：

TreeNode* deserialize(string data) {
    // 先获取节点信息
    vector<string> nodes;
    string tmp = "";
    for (auto ch : data)
    {
        if (ch == ',')
        {
            nodes.push_back(tmp);
            tmp = "";
        }
        else
            tmp.push_back(ch);
    }

    // 再反序列化
    return build(nodes);
}

TreeNode* build(vector<string>& nodes)
{
    if (nodes.empty())  
        return nullptr;

    // 找根节点
    string str = nodes[0];
    nodes.erase(nodes.begin());
    if (str == "#")
        return nullptr;
    int rootVal = stoi(str);

    // 递归构建左右子树
    TreeNode* root = new TreeNode(rootVal);
    root->left = build(nodes);
    root->right = build(nodes);

    return root;
}

后序遍历同理。

使用带空指针信息的层序遍历

我们也能使用带空指针信息的层序遍历来解决问题，参考代码如下：

void traverse(TreeNode* root, string& data)
{
    vector<TreeNode*> q;
    q.push_back(root);

    while (!q.empty())
    {
        vector<TreeNode*> nextQ;
        for (auto& cur : q)
        {
            if (cur == nullptr)
            {
                data += "#,";
                continue;
            }
            data += to_string(cur->val) + ",";
            nextQ.push_back(cur->left);
            nextQ.push_back(cur->right);
        }
        q.swap(nextQ);
        nextQ.clear();
    }
}

// Encodes a tree to a single string.
string serialize(TreeNode* root) {
    string data = "";
    traverse(root, data);
    return data;
}

// Decodes your encoded data to tree.
TreeNode* deserialize(string data) {
    // 先获取节点信息
    vector<string> nodes;
    string tmp = "";
    for (auto ch : data)
    {
        if (ch == ',')
        {
            nodes.push_back(tmp);
            tmp = "";
        }
        else
            tmp.push_back(ch);
    }

    // 再反序列化
    return build(nodes);
}

TreeNode* build(vector<string>& nodes)
{
    if (nodes.empty() || nodes[0] == "#")  
        return nullptr;

    int nodeIdx = 0;
    TreeNode* root = new TreeNode(stoi(nodes[nodeIdx++]));
    vector<TreeNode*> q;
    q.push_back(root);

    while (!q.empty())
    {
        vector<TreeNode*> nextQ;
        for (auto parent : q)
        {
            string tmp = nodes[nodeIdx++];
            if (tmp != "#")
            {
                parent->left = new TreeNode(stoi(tmp));
                nextQ.push_back(parent->left);
            }
            tmp = nodes[nodeIdx++];
            if (tmp != "#")
            {
                parent->right = new TreeNode(stoi(tmp));
                nextQ.push_back(parent->right);
            }
        }
        q.swap(nextQ);
        nextQ.clear();
    }

    return root;
}