准备春招，算法题冲冲冲！

区间合并

区间合并，就是将所有存在 交集 的区间进行一个合并。如图，五个蓝色的区间可以合并成三个绿色的区间：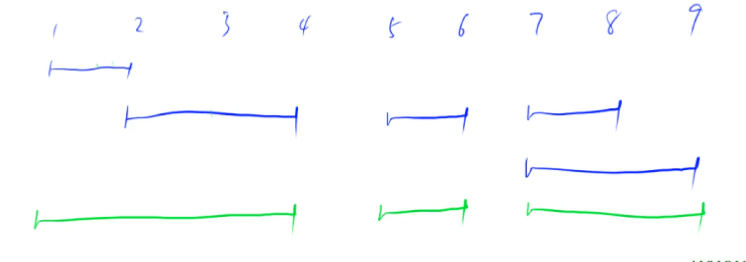

PS：若两个区间只有端点是相交的，这两个区间也能合并。

思路

1. 按区间左端点排序。
2. 扫描整个区间，把所有可能有交集的区间进行合并。

例如，当前所维护的区间如图：

可能有交集的区间如下：

• 在维护区间的内部，我们不做处理：

• 有交集（右侧突出），延长ed到突出的位置：

• 无交集，说明当前区间已经维护完毕，开始维护这个新区间：

代码

参考代码如下：

void merge(vector<pair<int, int>>& segs)
{
    vector<pair<int, int>> res;
    // 1.先对区间进行排序
    sort(segs.begin(), segs.end());
    // 2.开始区间合并
    int st = -2e9, ed = -2e9;	// 按题目范围自定义
    for (auto seg : segs)
    {
        // 情况3: 找到新区间
        if (ed < seg.first)
        {
            // 存储维护好的区间(最开始的除外)
            if (ed != -2e9)
            {
                res.push_back({st, ed});
            }
            // 开始维护新区间
            st = seg.first;
            ed = seg.second;
        }
        else
        {
            // 情况2: 有交集, 右侧突出
            ed = max(ed, seg.second);
        }
    }
    // 存储维护好的区间(最开始的除外) 
    if (st != -2e9)
    {
        res.push_back({st, ed});
    }
    
    segs = res;
}

例题

803. 区间合并 - AcWing题库

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

using PII = pair<int, int>;

void merge(vector<PII>& segs)
{
    vector<PII> ans;
    
    // 1. 排序区间
    sort(segs.begin(), segs.end());
    
    // 2. 进行区间合并
    int st = -2e9, ed = -2e9;
    for (auto [start, end] : segs)
    {
        // 情况3
        if (ed < start)
        {
            if (st != -2e9)
                ans.emplace_back(st, ed);
            st = start;
            ed = end;
        }
        else
        {
            // 情况2
            ed = max(ed, end);
        }
    }
    
    if (st != -2e9)
        ans.emplace_back(st, ed);
    
    segs = ans;
}

int main()
{
    int n, l, r;
    cin >> n;
    
    vector<PII> segs;
    segs.reserve(n);
    for (int i = 0; i < n; ++i)
    {
        cin >> l >> r;
        segs.emplace_back(l, r);
    }
    
    merge(segs);

    cout << segs.size();
}

56. 合并区间 - 力扣（LeetCode）

模板题

vector<vector<int>> merge(vector<vector<int>>& intervals) {
    int st = -1, ed = -1;
    vector<vector<int>> ans;
    ans.reserve(intervals.size());

    sort(intervals.begin(), intervals.end());
    for (auto& seg : intervals)
    {
        if (seg.at(0) > ed)
        {
            if (ed != -1)
            {
                ans.emplace_back(vector<int>({st, ed}));
            }
            st = seg.at(0);
            ed = seg.at(1);
        }
        else
        {
            ed = max(seg.at(1), ed);
        }
    }

    if (ed != -1)
    {
        ans.emplace_back(vector<int>({st, ed}));
    }

    return ans;
}

参考资料

• 算法基础课 - AcWing