3 - 前缀和与差分

发表于 2024-03-27 更新于 2024-04-22 分类于 cpp ，数据结构与算法， 1-基本算法阅读次数： Waline：本文字数： 6.3k 阅读时长 ≈ 5 分钟

准备春招，算法题冲冲冲！

前缀和与差分是一对逆运算，它们与高效区间操作有关。

前缀和Sn

概念

可以简单理解为 数组的前n项和，是一种重要的预处理方式，能大大降低查询的时间复杂度。

C++标准库中实现了前缀和函数std::partial_sum，详见这里，位于头文件<numeric>中。

构造

一维

例如有一数组A = {1, 2, 3, 4, 5}，要求一个数组S，满足S[n]为数组A的前n项和。

可通过递推实现：S[0] = A[0]，S[i] = S[i - 1] + A[i]。代码如下：

int a[] = {0, 1, 2, 3, 4, 5};
int s[6];

// 求前缀和(1起点)
for (int i = 1; i <= 5; ++i)
{
    s[i] = s[i - 1] + a[i];
}

使用std::partical_sum的代码如下：

vector<int> a = {1, 2, 3, 4, 5};
vector<int> s(a.size());

partial_sum(cbegin(a), cend(a), begin(s));

二维

int n, m, q;
cin >> n >> m >> q;

// 构造二维前缀和(1起点)
for (int i = 1; i <= n; ++i)
{
    for (int j = 1; j <= m; ++j)
    {
        cin >> a[i][j];
        s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
    }
}

区间求和操作

一维

可以通过前缀和快速求出原数组A里面一段数的和，例如要求[L, R]区间的元素和，只需计算S[R] - S[L-1]。

二维

如图，要想求二维前缀和S[i][j]（黑色填充部分），就得求绿色填充 + 红色填充 - 重叠部分 + A[i][j]。也就是：S[i][j] = S[i - 1][j] + S[i][j - 1] - S[i - 1][j - 1] + A[i][j]。

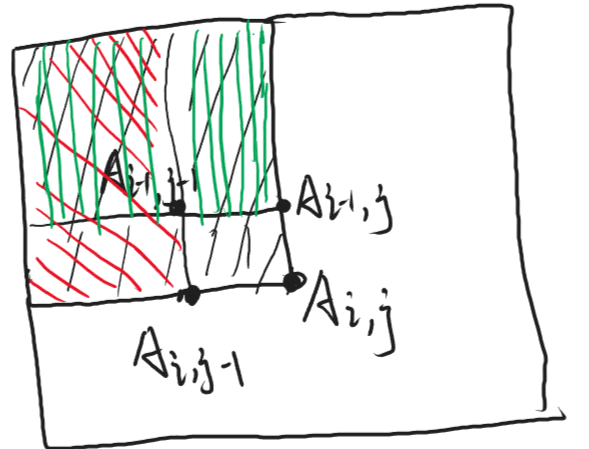
知道怎么求二维前缀和后，接下来看看如何运用它。例如，想求某矩阵的一块区间和（左上角[x1, y1]，右下角[x2, y2]），可以这样求：S[x2][y2] - S[x2][y1 - 1] - S[x1 - 1][y2] + S[x1 - 1][y1 - 1]。

例题

一维

795. 前缀和 - AcWing题库

#include <iostream>
using namespace std;

int a[100001], s[100001], n, m;

int main()
{
    cin >> n >> m;
    
    // 构造1起点的前缀和
    for (int i = 1; i <= n; ++i)
    {
        cin >> a[i];
        s[i] = s[i - 1] + a[i];
    }
    
    // 区间查询操作
    int l, r;
    for (int i = 0; i < m; ++i)
    {
        cin >> l >> r;
        cout << s[r] - s[l - 1] << '\n';
    }
}

209. 长度最小的子数组 - 力扣（LeetCode）

可以求出来数组的前缀和，然后去确定 前缀和 >= target的区间[i, j]。具体做法就是遍历前缀和中的每一个preSum[i - 1]，找到preSum[j]，使得preSum[j] - preSum[i - 1] >= target，找j的过程中可以用二分查找来加快速度。

int minSubArrayLen(int target, vector<int>& nums) {
    // 初始化前缀和(1起点)
    vector<int> preSum(nums.size() + 1, 0);
    for (int i = 1; i < preSum.size(); ++i)
    {
        preSum.at(i) = preSum.at(i - 1) + nums.at(i - 1);
    }

    // 找子数组
    int ans = 114514;
    for (int i = 1; i <= nums.size(); ++i)
    {
        auto j = lower_bound(preSum.begin(), preSum.end(), target + preSum.at(i - 1));
        if (j != preSum.end())
            ans = min<int>(j - preSum.begin() - i + 1, ans);
    }

    return ans == 114514 ? 0 : ans;
}

560. 和为 K 的子数组 - 力扣（LeetCode）

这道题可以用前缀和来做，用两层循环，统计preSum[i] - preSum[j - 1] == k的次数就行：

int subarraySum(vector<int>& nums, int k) {
    // 初始化前缀和
    vector<int> preSum(nums.size() + 1, 0);
    for (int i = 1; i <= nums.size(); ++i)
        preSum[i] = preSum[i - 1] + nums[i - 1];

    // 找答案
    int ans = 0;
    for (int i = 1; i <= nums.size(); ++i)
    {
        for (int j = 1; j <= i; ++j)
        {
            if (preSum[i] - preSum[j - 1] == k)
                ++ans;
        }
    }
    return ans;
}

但提交一看，耗时太大了，是的复杂度，有没有办法优化一下？

可以使用哈希表，和 两数之和 这道题一样，用哈希表存储前缀和的值，然后遍历一遍前缀和数组就行了：

int subarraySum(vector<int>& nums, int k) {
    int ans = 0;
    unordered_map<int, int> hash;			// 哈希表记录对应值的出现次数
    vector<int> preSum(nums.size() + 1, 0);

    // 子数组只有它一个元素
    hash[0]++;  
    for (int i = 1; i <= nums.size(); ++i)
    {
        preSum[i] = preSum[i - 1] + nums[i - 1];
        // preSum[i] - preSum[j - 1] = k  => preSum[j - 1] = preSum[i] - k 
        if (hash[preSum[i] - k])
            ans += hash[preSum[i] - k];

        hash[preSum[i]]++;
    }
    return ans;
}

二维

796. 子矩阵的和 - AcWing题库

#include <iostream>
using namespace std;

int a[1010][1010], s[1010][1010];

int main()
{
    int n, m, q;
    cin >> n >> m >> q;
    
    // 构造二维前缀和(1起点)
    for (int i = 1; i <= n; ++i)
    {
        for (int j = 1; j <= m; ++j)
        {
            cin >> a[i][j];
            s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
        }
    }
    
    // 区间求和操作
    int x1, x2, y1, y2;
    for (int i = 0; i < q; ++i)
    {
        cin >> x1 >> y1 >> x2 >> y2;
        
        cout << s[x2][y2] - s[x2][y1-1] - s[x1-1][y2] + s[x1-1][y1-1]  << '\n';
    }
}

差分Bn

概念

可看做前缀和的逆运算，例如有数组A = {a1, ... ,an}，那么B[n] = A[n] - A[n - 1], B[1] = A[1]。

从上面可以发现，A[n]的值是B的前缀和/前n项和。

差分数组的主要使用场景是 对原始数组的某个区间的元素进行增减。

区间插入操作（区间增减）

一维

给A[L] ~ A[R]都+ c，那么仅需：

void insert(int L, int R, int c)
{
    b[L] += c;				// 让A[L] ~ A[n]都被+c
    
    // 这里注意数组越界问题
    if (R + 1 < diff.size())
    	b[R + 1] -= c;		// 让A[R+1] ~ A[n]恢复原状
}

二维

可由一维类推得到，如下图所示：

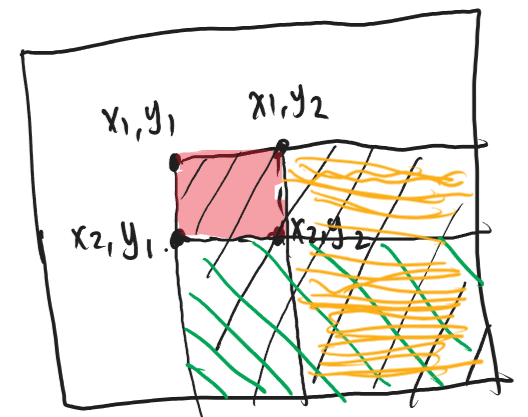
要想给A[x1][y1] ~ A[x2][y2]都+ c，那么仅需：

void insert(int x1, int y1, int x2, int y2, int c)
{
    b[x1][y1] += c; 		// a[x1][y1] ~ a[n][m] + c
    b[x2 + 1][y1] -= c;		// a[x2+1][y1] ~ a[n][m] - c
    b[x1][y2 + 1] -= c;		// a[x1][y2+1] ~ a[n][m] - c
    b[x2 + 1][y2 + 1] += c;	// a[x2+1][y2+1] ~ a[n][m] + c
}

构造

可以利用区间插入操作来构造差分，分一维和二维讨论。

一维

要想构造一维的差分，可在[1, 1]处插入a[0]，… ，在[n, n]处插入a[n - 1]。

接下来就能对差分进行区间操作了，如果想要获得操作后的a[n]，仅需对b[n]求前缀和：

for (int i = 1; i <= n; i++)
    b[i] += b[i-1];

二维

和一维同理，求前缀和代码如下：

for (int i = 1; i <= N; i++)
    for (int j = 1; j <= M; j++)
        b[i][j] += b[i-1][j] + b[i][j-1] - b[i-1][j-1];

例题

一维

797. 差分 - AcWing题库

#include <iostream>
using namespace std;

int a[100010], b[100010];

void insert(int l, int r, int c)
{
    b[l] += c;
    b[r + 1] -= c;
}

int main()
{
    int n, m;
    cin >> n >> m;
    
    // 构造差分(1起点)
    for (int i = 1; i <= n; ++i)
    {
        cin >> a[i];
        insert(i, i, a[i]);
    }
    
    // 区间操作
    int l, r, c;
    for (int i = 0; i < m; ++i)
    {
        cin >> l >> r >> c;
        insert(l, r, c);
    }
    
    // 得到操作后的A[n]
    for (int i = 1; i <= n; ++i)
    {
        b[i] += b[i - 1];
        cout << b[i] << " ";
    }
}

370. 区间加法 - 力扣（LeetCode）

差分模板题：

void insert(vector<int>& diff, int L, int R, int c)
{
    diff[L] += c;
    if (R + 1 < diff.size())
        diff[R + 1] -= c;
}

vector<int> getModifiedArray(int length, vector<vector<int>>& updates) {
    vector<int> diff(length, 0);

    // 构建差分数组
    for (auto& update : updates)
        insert(diff, update[0], update[1], update[2]);

    // 从差分数组构建修改后的区间
    for (int i = 1; i < length; ++i)
        diff[i] += diff[i - 1];

    return diff;
}

1109. 航班预订统计 - 力扣（LeetCode）

差分模板题，套了个情景，参考代码如下：

void insert(vector<int>& diff, int L, int R, int c)
{
    diff[L] += c;
    if (R + 1 < diff.size())
        diff[R + 1] -= c;
}

vector<int> corpFlightBookings(vector<vector<int>>& bookings, int n) {
    vector<int> diff(n, 0);

    // 构建差分数组(注意booking里的是1起点)
    for (auto& booking : bookings)
        insert(diff, booking[0] - 1, booking[1] - 1, booking[2]);

    // 还原修改后的区间
    for (int i = 1; i < n; ++i)
        diff[i] += diff[i - 1];

    return diff;
}

1094. 拼车 - 力扣（LeetCode）

我们可以将乘客接放的位置看成一个大区间（1~1000），然后开始模拟。例如[2,1,5]的意思就是把区间[1, 5)中所有元素+2。

代码如下：

void insert(vector<int>& diff, int L, int R, int c)
{
    diff[L] += c;
    if (R + 1 < diff.size())
        diff[R + 1] -= c;
}

bool carPooling(vector<vector<int>>& trips, int capacity) {
    // 构建差分数组
    vector<int> diff(1001, 0);
    for (auto& trip : trips)
        // 注意在[L, R)中修改, 就是在[L, R - 1]中修改
        insert(diff, trip[1], trip[2] - 1, trip[0]);

    // 获取修改后区间
    for (int i = 1; i < diff.size(); ++i)
    {
        diff[i] += diff[i - 1];
    }

    for (int i = 0; i < diff.size(); ++i)
    {
        if (diff[i] > capacity)
            return false;
    }

    return true;
}

二维

798. 差分矩阵 - AcWing题库

#include <iostream>
using namespace std;

int b[1010][1010];

void insert(int x1, int y1, int x2, int y2, int c)
{
    b[x1][y1] += c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y1] -= c;
    b[x2 + 1][y2 + 1] += c;
}

int main()
{
    int n, m, q;
    cin >> n >> m >> q;
    
    // 构造二维差分 (1起点)
    int c;
    for (int i = 1; i <= n; ++i)
    {
        for (int j = 1; j <= m; ++j)
        {
            cin >> c;
            insert(i, j, i, j, c);
        }
    }
    
    // 区间插入操作
    int x1, y1, x2, y2;
    for (int i = 0; i < q; ++i)
    {
        cin >> x1 >> y1 >> x2 >> y2 >> c;
        insert(x1, y1, x2, y2, c);
    }
    
    // 求操作后的a
    for (int i = 1; i <= n; ++i)
    {
        for (int j = 1; j <= m; ++j)
        {
            b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];
            cout << b[i][j] << " ";
        }
        cout << '\n';
    }
}

参考资料

算法基础课 - AcWing
前缀和 & 差分 - OI Wiki (oi-wiki.org)