2 - 二分
准备春招,算法题冲冲冲!
如果要在有序序列中查找我们想要的东西,顺序查找很浪费时间,而且也浪费了“有序”这一性质。而使用 二分 可以利用输入的有序性,快速得到答案。
二分
思想
找到某种性质,该性质可以让输入序列呈现“有序”状态(例如单增、单减啥的)。再将这种性质作具体要求,可以将序列一分为二:

红色为不满足/满足性质的,绿色为满足/不满足性质的,二分可以找到它们的分界点,常用来解决一些边界问题。
整数二分
首先是闭区间[Left, Right]形式,如图:

刚开始取0处为L,5处为R,那么有 M = L + (R - L) / 2 = 2。这里不直接写(L + R) / 2的目的是防止加法计算溢出。
接下来如果想找红色部分(lower_bound()),让L = M + 1,然后更新M;如果想找绿色部分(upper_bound()),让R = M - 1,然后更新M。最后R<L说明二分查找结束,L或R为要找的答案。
参考代码如下:
// 满足性质的判断函数
bool check() { }
int binarySearch(int arr[], int n)
{
int left = 0;
int right = n - 1; // [L, R]
while (left <= right)
{
int mid = left + (right - left) / 2;
if (check())
right = mid - 1; // [L, M - 1]
else
left = mid + 1; // [M + 1, R]
}
return left;
}然后是开区间的形式:
[L, R):R为6,更新R时R = M,当L == R时结束查找,L和R均指向答案。(L, R]:L为-1,更新L时L = M,当L == R时结束查找,L和R均指向答案。(L, R):L为-1,R为6,更新L时L = M,更新R时R = M,当L + 1 == R时结束查找,R指向答案。
浮点数二分
和整数二分类似,就是有关浮点数比较的部分要注意。当区间长度足够小时 (\(r-l\leq10^{-8}\)) ,可以直接用 l 当作二分答案:
| 题目要求 | 精度 |
|---|---|
| 保留四位小数 | 1e-6 |
| 保留五位小数 | 1e-7 |
| 保留六位小数 | 1e-8 |
例题
上面的可能没解释清楚,还是来看看例题吧!
二分查找
二分思想最典型的应用,查找目标值。
数的三次方根 - AcWing
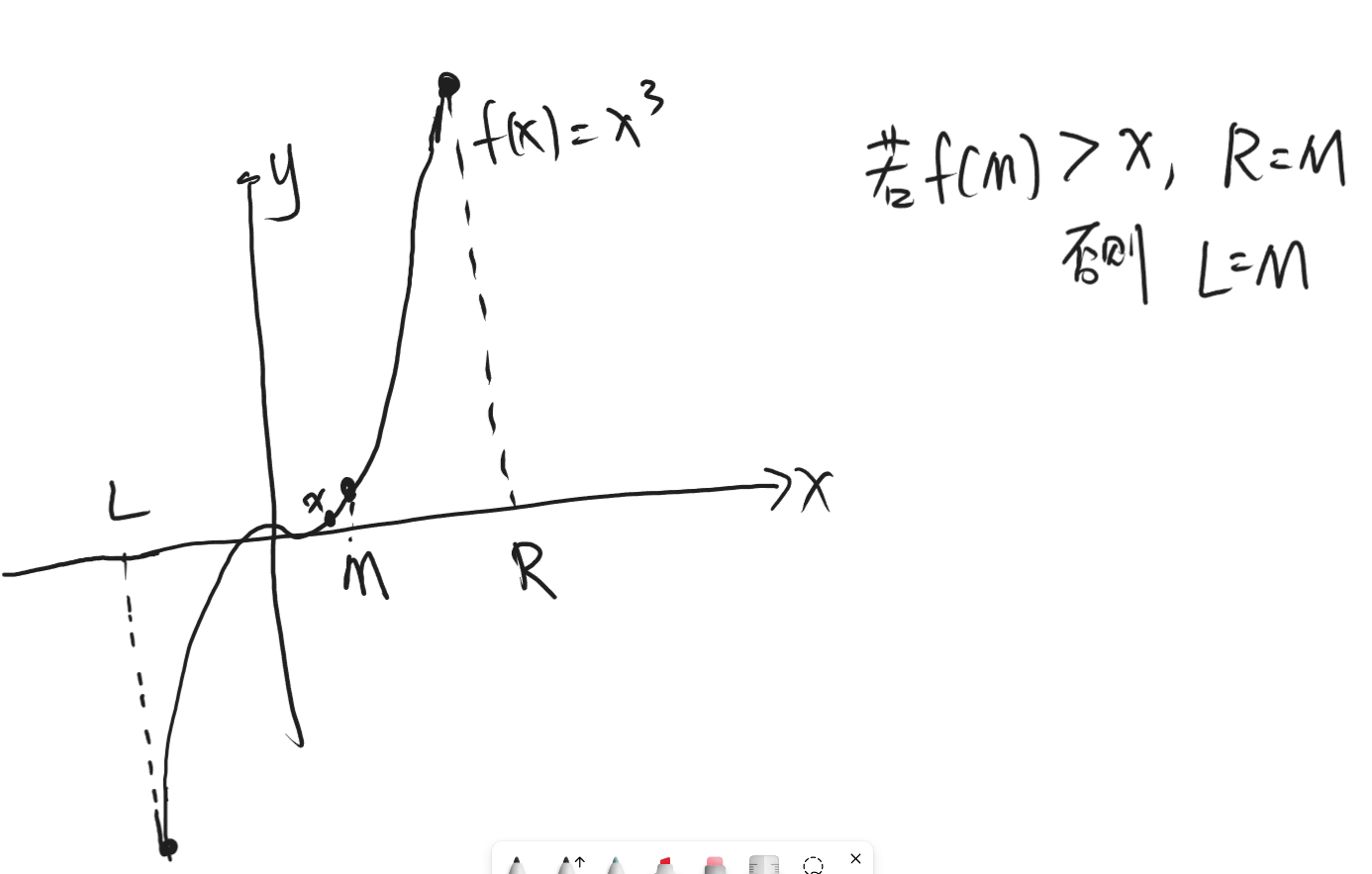
如图所示,可以通过二分的方式找到数的三次方根,注意按格式输出以及有关函数在哪个头文件定义。
#include <iostream>
#include <iomanip> // setprecision()
#include <cmath> // fabs()
using namespace std;
int main()
{
double n;
cin >> n;
double l = -10000.0, r = 10000.0;
while (fabs(l - r) >= 1e-7)
{
double mid = l + (r - l) / 2.0;
if (mid * mid * mid >= n)
r = mid;
else
l = mid;
}
cout << fixed << setprecision(6) << l;
}二分答案
275. H 指数 II - 力扣(LeetCode)
先确定二分的取值范围,由于答案h是论文篇数,那么有 \[ \nonumber 0 \leq h \leq \mathrm{cit.size()} \] 接下来利用开区间的二分函数模板,确定
Left = 0(不为-1的原因是负数答案无意义),Right = cit.size() + 1。然后要 在问题中找到令其“有序”的规律,就是找循环不变量。本题的循环不变量是:h是不是h指数。
例如,如果h=3是h指数,那么h=2,h=1,h=0也是h指数;如果h=4不是h指数,那么h=5,h=6,…,都不是h指数。
因此有:
Left及其之前的均为h指数,Right及其之后的均不是h指数。
接下来以输入示例1为例,看看二分的过程:
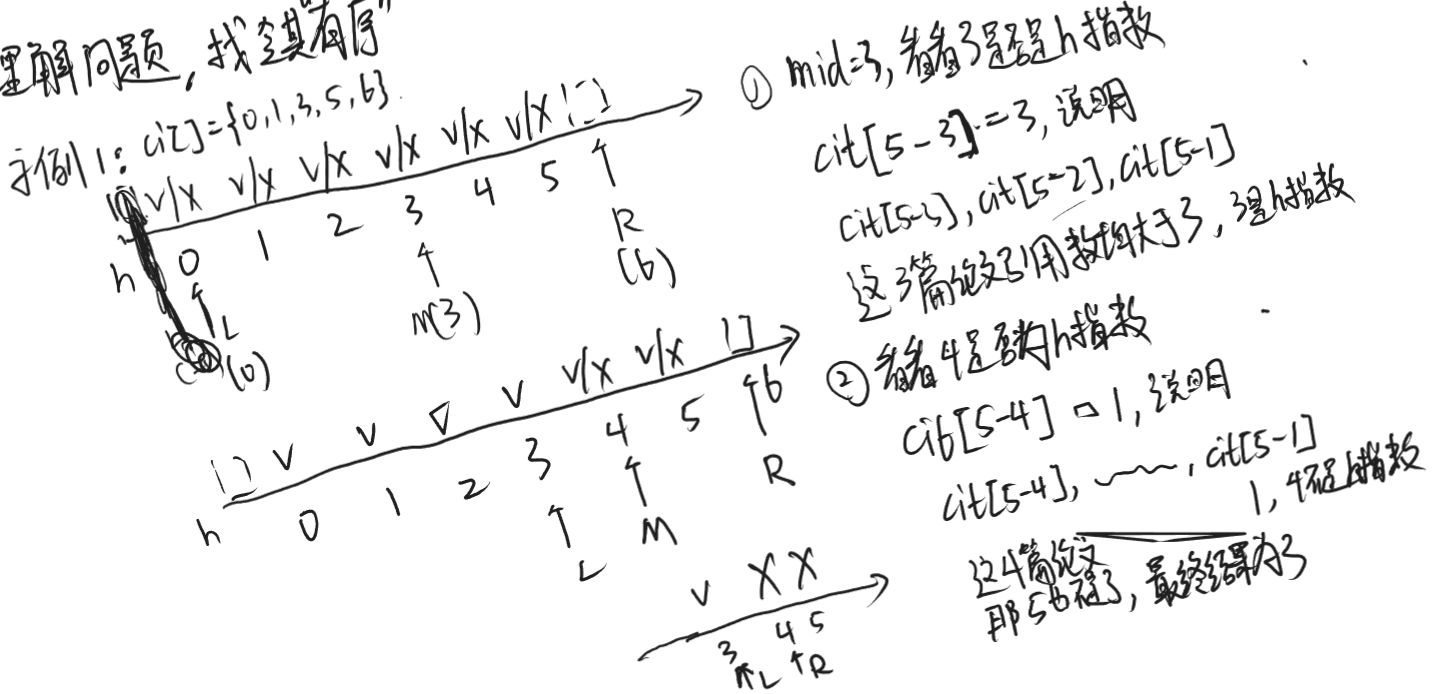
参考代码如下:
int hIndex(vector<int>& citations) {
int l = 0, r = citations.size() + 1;
while (l + 1 < r)
{
int mid = l + (r - l) / 2;
if (citations.at(citations.size() - mid) >= mid)
l = mid;
else
r = mid;
}
return l;
}1283. 使结果不超过阈值的最小除数 - 力扣(LeetCode)

参考代码如下:
int getSum(vector<int>& nums, int div)
{
int sum = 0;
for (auto& x : nums)
{
sum += ceil(static_cast<double>(x) / div);
}
return sum;
}
int smallestDivisor(vector<int>& nums, int threshold) {
// 先排序
sort(nums.begin(), nums.end());
// 再二分
int l = 0, r = nums.at(nums.size() - 1) + 1;
while (l + 1 < r)
{
int mid = l + (r - l) / 2;
if (getSum(nums, mid) > threshold)
l = mid;
else
r = mid;
}
return r;
}2187. 完成旅途的最少时间 - 力扣(LeetCode)

发现自己对二分题目有点自信了,但还是不怎么熟悉。本题主要是裁到 找到合适的取值范围 这一步了,看题目范围是1 ~ 10^7,就以为是这个范围,实际上应该是1 ~ time.max() * totaltrips。此外还要注意数据类型是long long,否则计算过程中会发生溢出,导致答案错误。
参考代码如下:
long long minimumTime(vector<int>& time, int totalTrips) {
long long l = 0;
long long r = static_cast<long long>(*max_element(cbegin(time), cend(time))) * static_cast<long long>(totalTrips) + 1LL;
while (l + 1 < r)
{
long long m = l + (r - l) / 2;
// cout << l << " " << m << " " << r << '\n';
long long trips = 0;
for_each(cbegin(time), cend(time), [&m, &trips](int v1) {trips += m / v1;});
// cout << trips << "\n";
if (trips < totalTrips)
l = m;
else
r = m;
}
return r;
}2226. 每个小孩最多能分到多少糖果 - 力扣(LeetCode)
1870. 准时到达的列车最小时速 - 力扣(LeetCode)
1011. 在 D 天内送达包裹的能力 - 力扣(LeetCode)
875. 爱吃香蕉的珂珂 - 力扣(LeetCode)
1898. 可移除字符的最大数目 - 力扣(LeetCode)
最小化最大值
数的范围 - AcWing
需要进行两次二分查找,第一次需要找该元素的起始位置,第二次需要找该元素的终止位置。
首先是第一次寻找,这里使用(left, right)的二分模板。如果arr[mid] < x,就让left = mid,否则让right = mid,当left + 1 == right时退出循环。如图,寻找第一个3的过程如下:
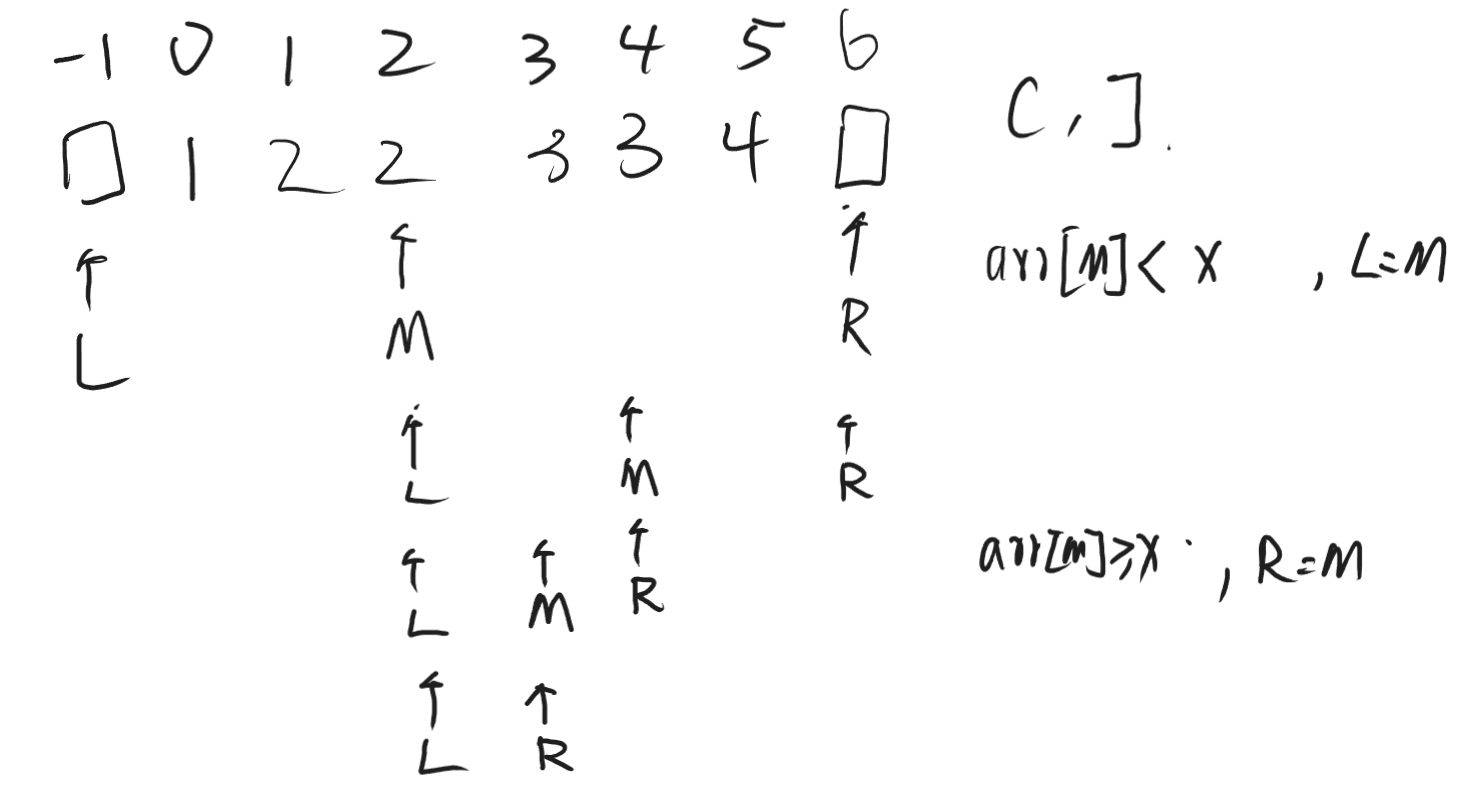
然后是第二次寻找,条件为arr[mid] <= x。如图,寻找第二个3的过程如下:
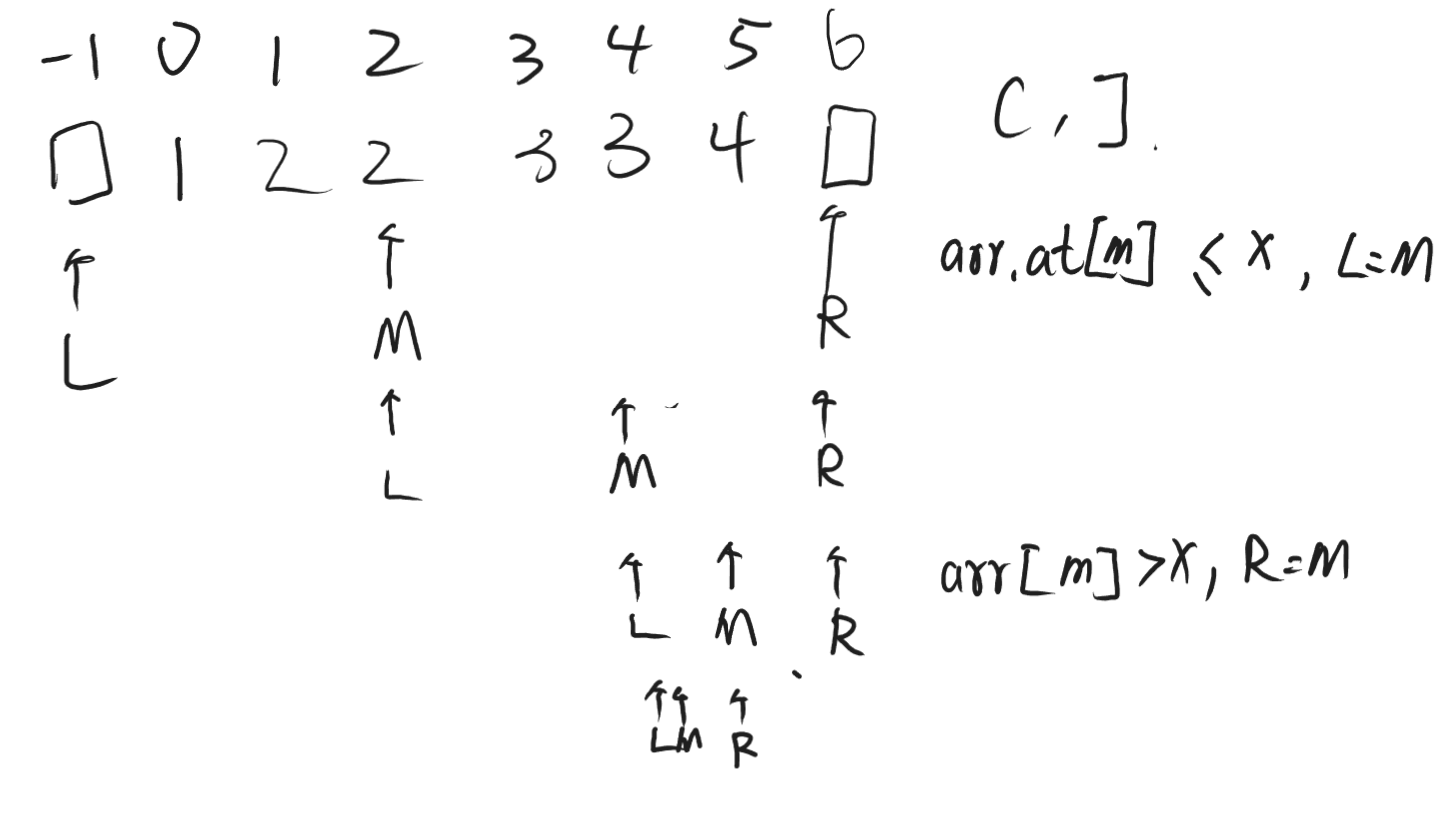
参考代码如下:
#include <vector>
#include <iostream>
using namespace std;
int findFirstX(const vector<int>& arr, int x)
{
int ans = -1;
// (left, right)
int left = -1, right = arr.size(), mid = 0;
while (left + 1 < right)
{
mid = left + (right - left) / 2;
if (arr.at(mid) < x)
left = mid;
else
right = mid;
}
// 找不到
if (right < arr.size() && arr.at(right) == x)
ans = right;
return ans;
}
int findLastX(const vector<int>& arr, int x)
{
int ans = -1;
// (left, right)
int left = -1, right = arr.size(), mid = 0;
while (left + 1 < right)
{
mid = left + (right - left) / 2;
if (arr.at(mid) <= x)
left = mid;
else
right = mid;
}
if (left < arr.size() && arr.at(left) == x)
ans = left;
return ans;
}
int main()
{
int n, q;
cin >> n >> q;
vector<int> arr(n);
for (int i = 0; i < n; ++i)
cin >> arr.at(i);
for (int i = 0; i < q; ++i)
{
cin >> n;
int firstX = findFirstX(arr, n);
int lastX = findLastX(arr, n);
cout << firstX << " " << lastX << '\n';
}
}除此之外,我们还能用标准库的二分查找算法来解决这道题:
lower_bound():该算法在有序范围内查找不小于 (大于等于) 给定值的第一个元素。upper_bound():查找有序序列中大于给定值的第一个元素。
根据这两个算法的描述,发现前者可用于第一次查找,直接用就行;后者可用于第二次查找,需要返回结果的前一项,参考代码如下:
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
int main()
{
int n, q;
cin >> n >> q;
vector<int> arr(n);
for (int i = 0; i < n; ++i)
cin >> arr.at(i);
for (int i = 0; i < q; ++i)
{
cin >> n;
int firstX = lower_bound(begin(arr), end(arr), n) - begin(arr);
int lastX = upper_bound(begin(arr), end(arr), n) - begin(arr) - 1;
if (firstX <= lastX)
cout << firstX << " " << lastX << '\n';
else
cout << -1 << " " << -1 << "\n";
}
}5566. 盖楼 - AcWing题库
这道题是个数学问题,需要用二分来简化时间复杂度。
首先来解决数学问题,假设给定楼层mid用来分配,那么:
- 只能被X整除:
onlyX = mid / x - gcd(x, y)。由于在这里x和y都是质数,那么gcd(x, y) = x * y。那么onlyX = mid / x - mid / x / y。 - 只能被Y整除:
onlyY = mid / x - mid / x / y。 - 剩下空余的楼层:
remaining = mid - onlyX - onlyY - mid / x / y
接下来将onlyY分配给n;将onlyX分配给m,那么就会剩下max(0, n - onlyY) + max(0, m - onlyX)。将remaining和前者比较,如果remaining比不于前者,说明这个mid合理。
#include <iostream>
#include <vector>
using namespace std;
int n, m, x, y;
bool check(int mid)
{
int onlyY = mid / y - mid / x / y;
int onlyX = mid / x - mid / x / y;
int ramaining = mid - onlyX - onlyY - mid / x / y;
return ramaining >= max(n - onlyY, 0) + max(m - onlyX, 0);
}
int main()
{
cin >> n >> m >> x >> y;
int l = 0, r = 1e9 + 1;
while (l + 1 < r)
{
int mid = l + (r - l) / 2;
if (check(mid))
r = mid;
else
l = mid;
}
cout << r;
}最大化最小值
第k小/大
其他
1146. 快照数组 - 力扣(LeetCode)
按一般思路,每次进行snap()操作后,都需要对原数组复制一次,而这样明显会超空间。
因此应该存储对索引的历史情况(也就是只存储离散的要修改元素,而不是整个数组),然后查找索引的历史情况时,由于snapID是升序的,可以用二分提高查找效率。
参考代码如下:
class SnapshotArray {
public:
SnapshotArray(int length)
: m_snapId(0) {}
void set(int index, int val) {
m_indexHistory[index].push_back({m_snapId, val});
}
int snap() {
return m_snapId++;
}
int get(int index, int snap_id) {
vector<pair<int, int>>& history = m_indexHistory[index];
// 二分查找
int l = -1, r = history.size();
while (l + 1 < r)
{
int mid = l + (r - l) / 2;
// 这里让id+1是因为找的是id的最新历史,
// 找到id+1的前一个元素就是id的最新历史
if (history[mid].first >= snap_id + 1)
r = mid;
else
l = mid;
}
return l < 0 ? 0 : history[l].second;
}
private:
int m_snapId;
unordered_map<int, vector<pair<int, int>>> m_indexHistory;
};参考资料
- 算法基础课 - AcWing
- 分享丨【题单】二分算法(二分答案/最小化最大值/最大化最小值/第K小) - 力扣(LeetCode)