01 - 游戏引擎的动画技术基础
本文将对游戏引擎中的动画技术基础做一些介绍,比如游戏相关的动画技术有什么,要用到的数学知识(空间坐标系、3D旋转),蒙皮动画的实现,动画的压缩,动画制作流程等。
动画技术总览
早期2D游戏使用Sprite动画技术,画出每帧动画的图像,然后逐帧播放(Doom也是2D游戏,但它通过对2D图像做变换让你以为自己在3D世界中):

接下来进入3D游戏时代,借助显卡加持,出现了骨骼动画、蒙皮动画、基于物理的动画等技术:

遇到的挑战
游戏动画要和玩家输入与Gameplay机制配合,如何及时反应很重要:

游戏引擎都是实时计算的,如何优化动画在内存的读取等耗时内容很重要:

随着人们对游戏要求越来越高,动画也被要求越来越真实:

2D动画技术
Sprite动画
将动画的所有帧画出来,然后重复播放即可,这就是Sprite动画。
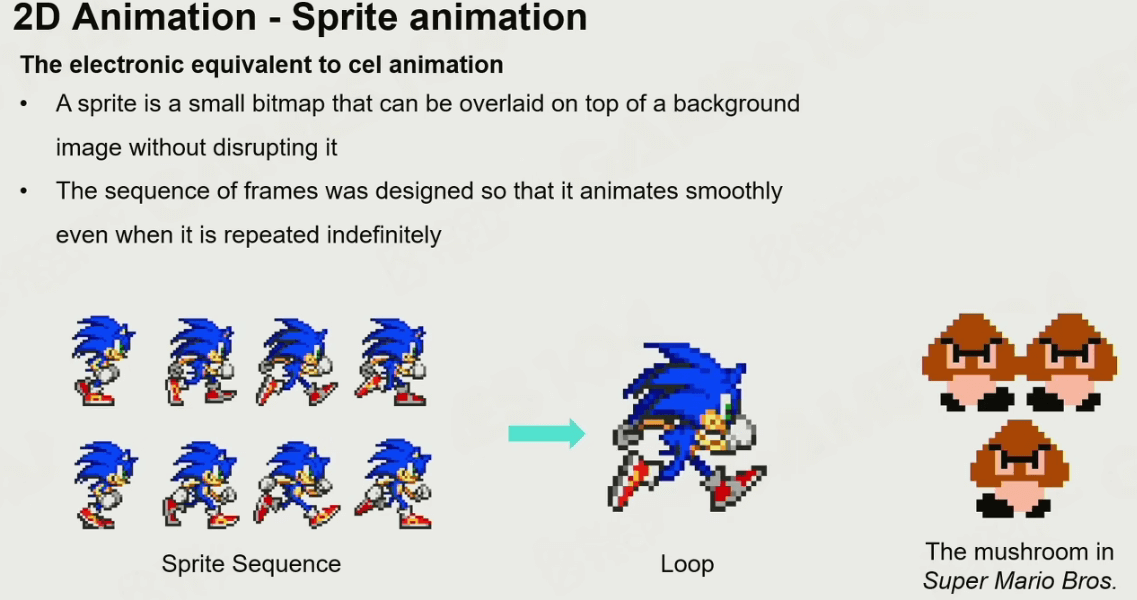
一些伪3D游戏则会额外画一些不同角度的动画,并根据摄像机相对它的位置选择性播放。

现在,Sprite动画技术主要用于粒子系统的动画等。

Live2D

Live2D将一张张小图片组合起来,通过仿射变换让它们“动起来”。

要想制作Live2D动画,首先要预处理资源,例如通过预处理资源的深度来正确处理遮挡关系。

处理好资源后,就能通过编辑控制点和网格来变换这些图片,以达到“动”的目的。
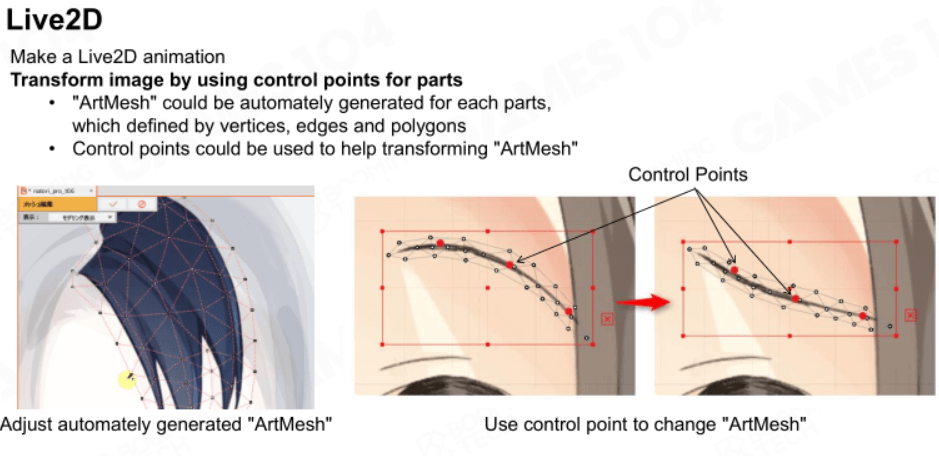
只需要在关键帧处进行变换就行,这个操作也被称为K帧。

3D动画技术
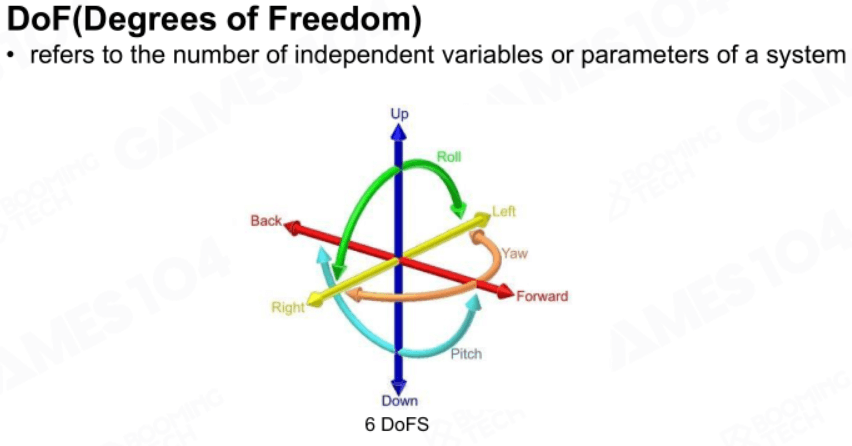
自由度DoF
就是一个物体可以变化的维度,一般来说有9个自由度,平移3个,旋转3个,放缩3个。
层级刚体动画
是最早期的3D动画,通过层级结构管理角色的骨骼,然后以骨骼为单位去做动画。但骨骼间可能会出现“穿模现象”。

顶点动画
是除物理模拟布料/水体外的另一种选择,将物体每个顶点位置随时间的变化存起来(一张平移贴图,一张旋转贴图),然后在运行时读取并“模拟”。

形变动画
和传统顶点动画类似,但添加了顶点影响权重,用于在不同关键帧间给顶点动画插值。通常用于人物表情领域。

蒙皮动画
这是目前广泛运用的技术,利用刚体骨骼和包在骨骼上的蒙皮驱动动画,看上去更自然。

在3D基础上延伸,蒙皮动画也能应用到2D游戏中。

基于物理的动画
例如布娃娃系统,布料模拟,反向动力学IK,为了追求更真实的动画,现在不少游戏开始应用基于物理的动画。

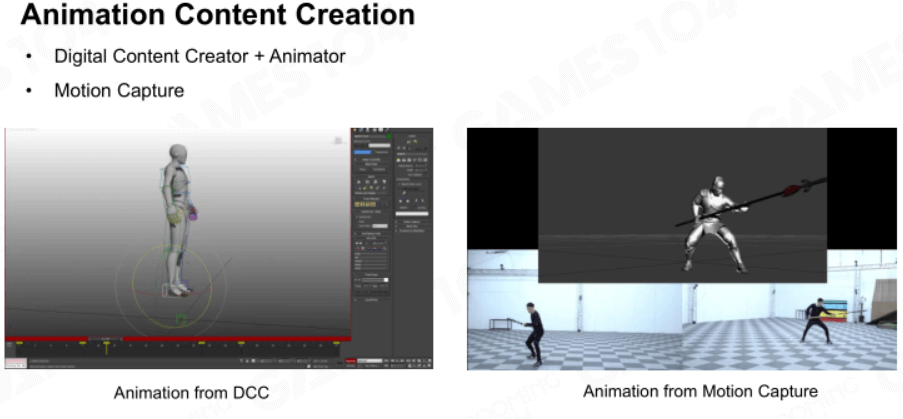
动画的制作
动画的制作分为传统手k动画和较新的动作捕捉:
预备知识
不同的空间系
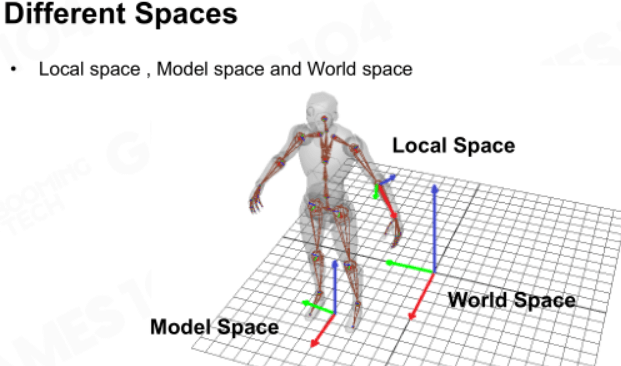
需要在各自的空间里进行动画计算,主要有三种空间:
- 世界空间:描述所有物体在世界的坐标,尺度可以很大。
- 模型空间:模型自己的坐标系,尺度一般较小。
- 局部空间:在动画里每根骨骼自己的坐标系。
设立这么多空间坐标系就是为了方便后续表达和计算。
旋转
Ps:有关旋转的数学内容,详见我的GAMES101文章。
2D旋转
2D旋转的推导如下,可以将旋转表达成矩阵:

3D旋转
绕三个轴单独旋转的推导如下:

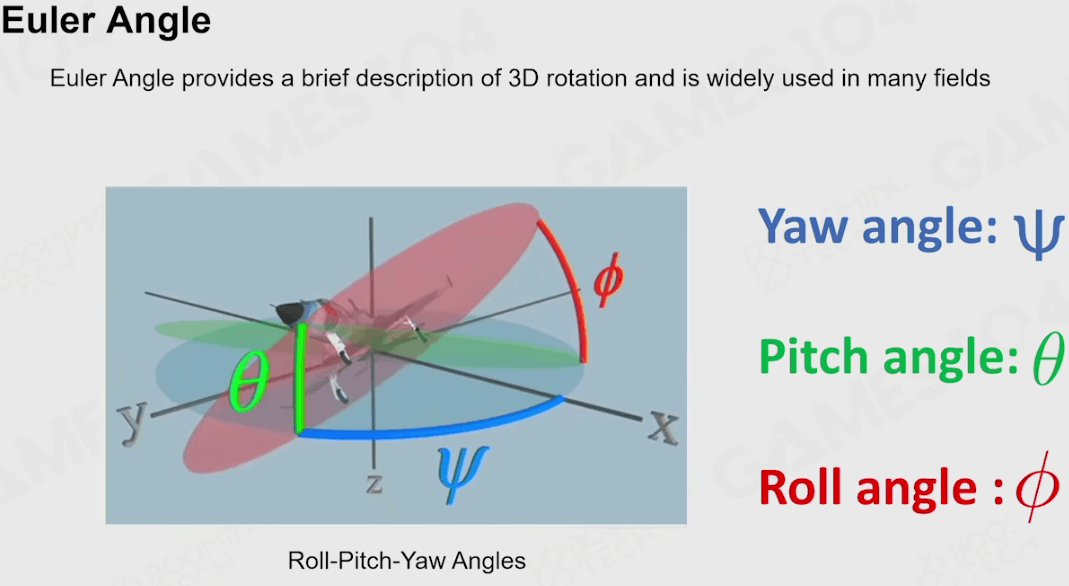
欧拉角
因此欧拉角便出现了,通过用三个角度描述物体的旋转。
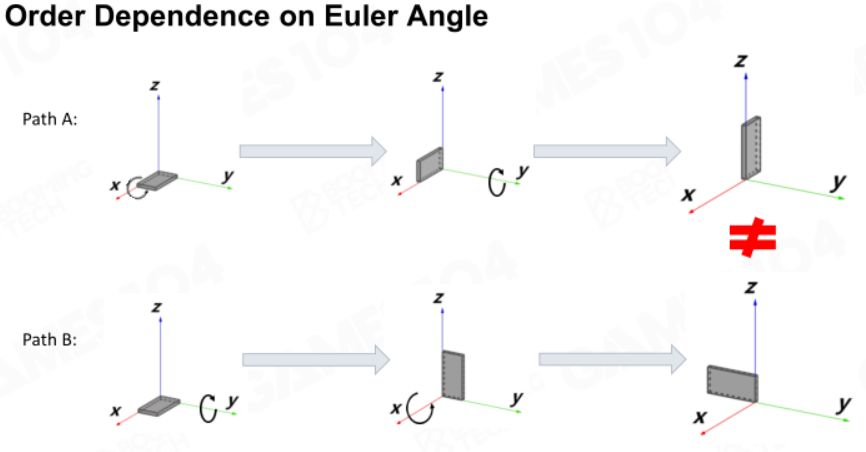
欧拉角的问题很多,首先是顺序问题:相同数值不同运算顺序得到的结果是不相同的。因此得规定好旋转的顺序。
然后是万向节死锁问题,当俯仰角为90°时,旋转其他两个角的效果一样。

用矩阵角度解释如下:

总的来说,使用欧拉角描述3D旋转有如下问题:
- 万向节死锁问题:会少一个自由度;
- 插值困难:旋转间角度插值是困难的;
- 旋转的叠加困难:需要相关矩阵计算;
- 很难做定轴运算:不能绕任意轴旋转。
四元数
3D空间的旋转也能用四元数来描述:

四元数的旋转如下:


四元数可以绕任意轴旋转:

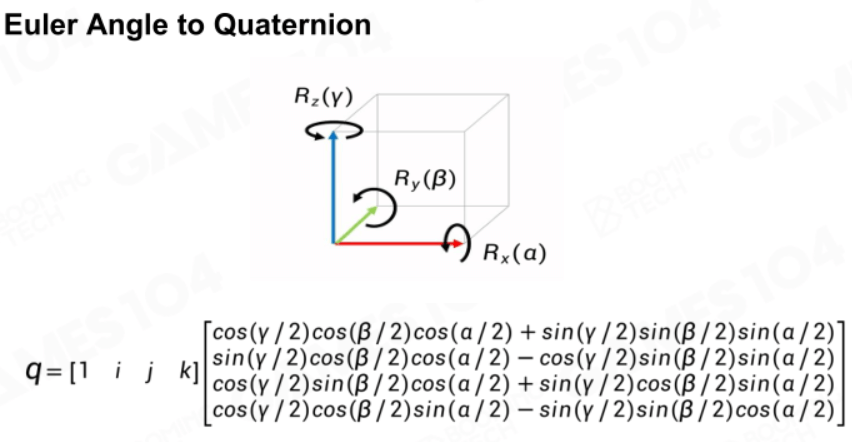
四元数和欧拉角:
四元数和矩阵:

蒙皮动画的实现
总体步骤

制作蒙皮动画的步骤如下:
- 准备一个处于绑定姿势的模型;
- 为这个模型做一个骨架;
- 给骨架刷上对应的蒙皮;
- 给骨架制作动画姿势;
- 通过骨架和蒙皮权重让模型动起来。
骨架
骨架(Skeleton)可以分为两种,人形骨架和非人形骨架。骨架由层次结构管理,最靠近根节点的骨骼一般在胯部(脊柱尾椎骨)。
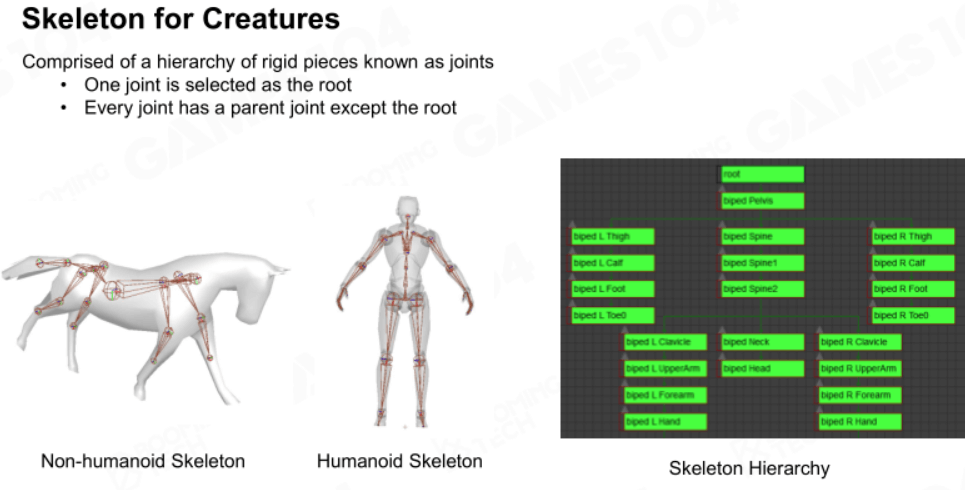
关节与骨骼
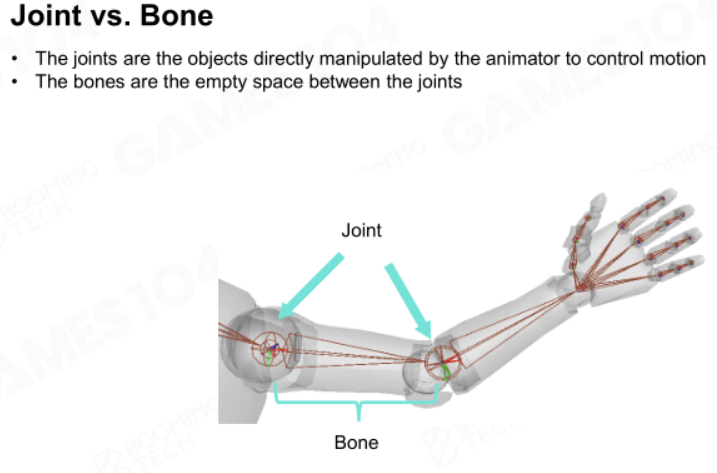
关节(Joint)和骨骼(Bone)不一样,关节是连接骨骼的节点,且存储和它相连骨骼的信息。关节有自由度,骨骼没有。
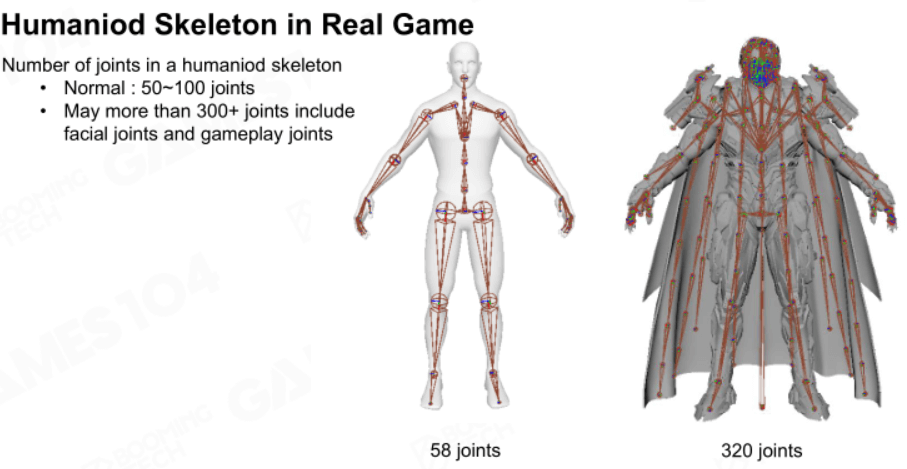
人形骨架
一般都是先准备一个标准人形骨架,然后基于此骨架准备动画。例如在给它添加装备时(如披风、变形武器等)将装备的骨架也附加到人形骨架上。
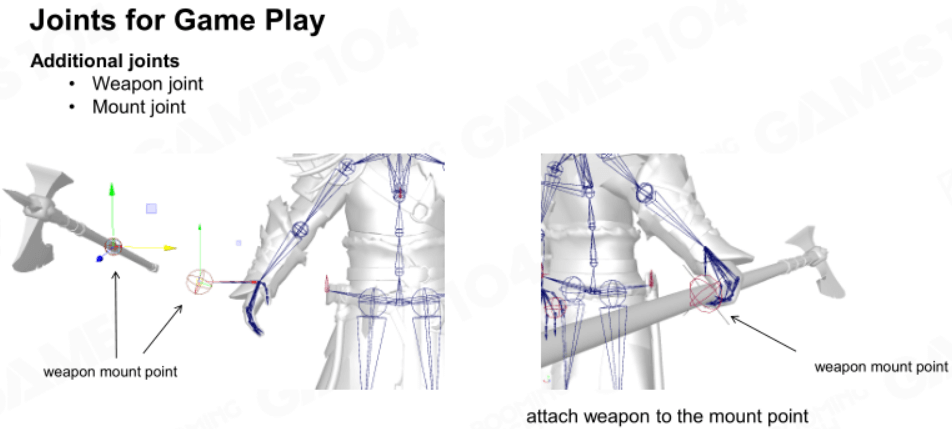
武器关节
正如上边说的,武器可以将其关节附着在人体骨架的锚点上。
人形骨架的根节点
人形骨架的根节点一般定义在两脚之间,它很容易与地面接触,方便人们调整移速。
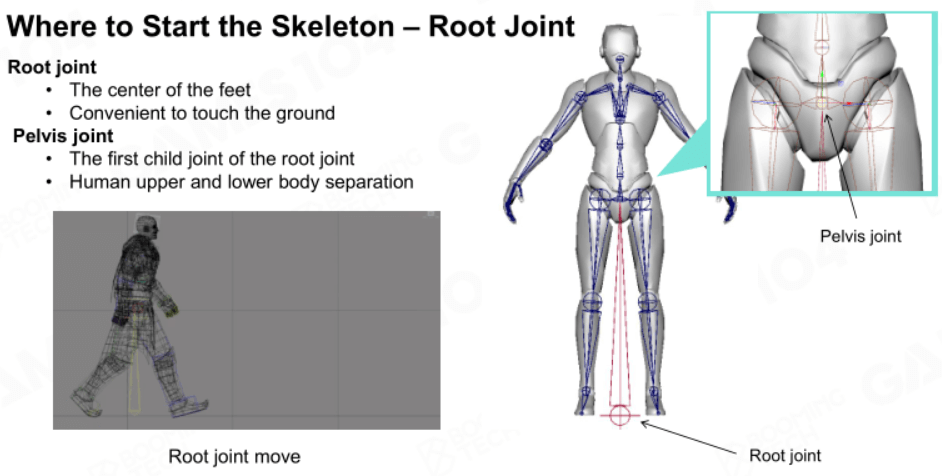
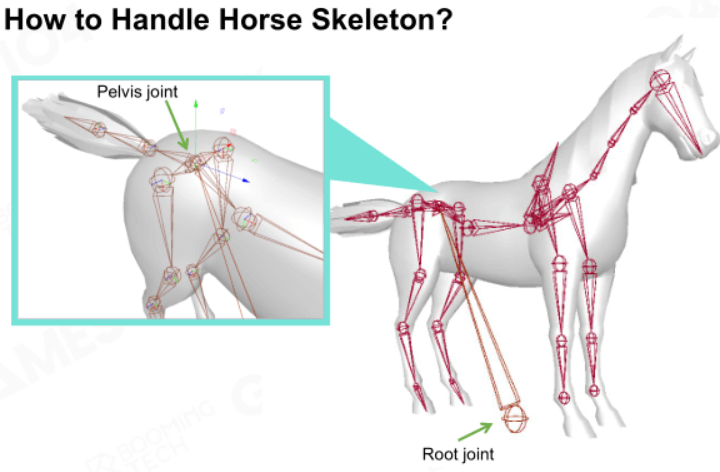
非人形骨架的根节点
非人形骨架的根节点和人形骨架类似,都在尾椎骨关节(Pelvis Joint)朝向n只脚中间的地面上。
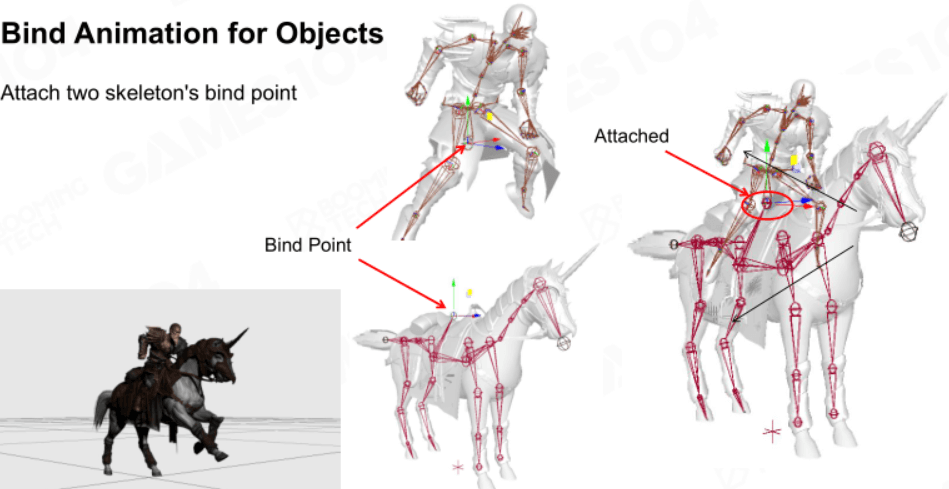
绑定
为对象绑定动画
例如将人和马绑定在一起,同时播放它们自己的动画,看起来就是人在骑马。这需要将人和马的绑定点重合,不论是平移还是旋转都要重合。
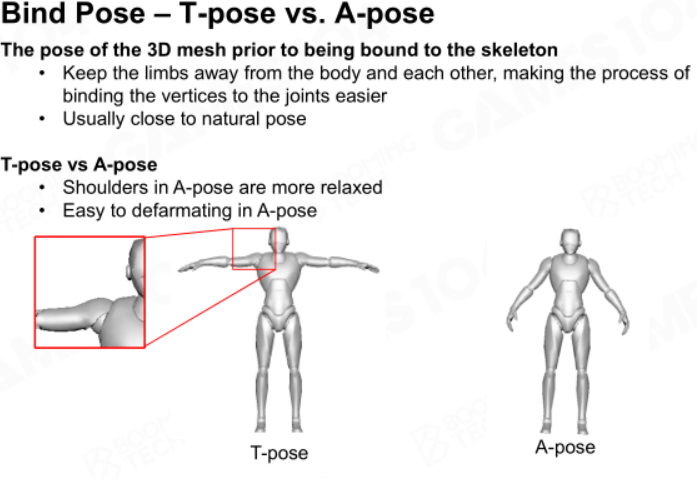
绑定姿势
绑定姿势有T-Pose和A-Pose两种,不过人们更偏向用A-Pose,因为T-Pose对肩膀过于挤压了。
骨架姿势
有了基本的绑定姿势,就能通过变换每个关节的自由度来定义骨架的姿势了。
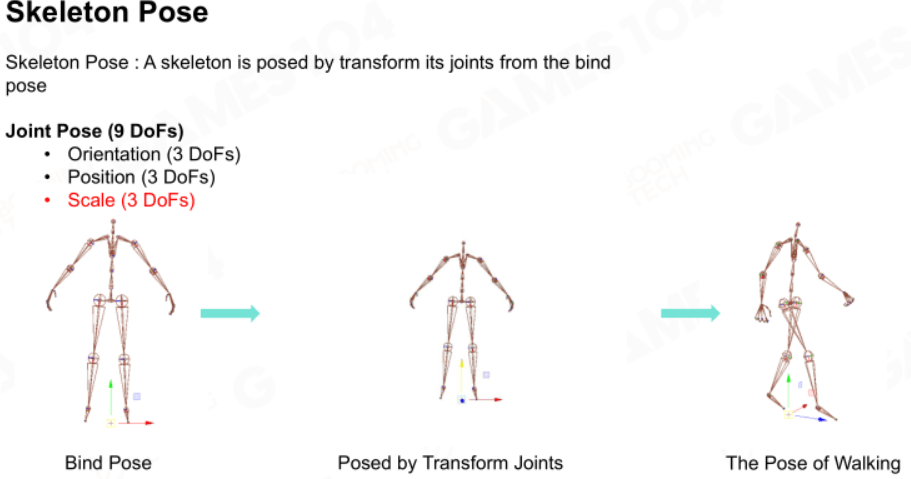
关节姿态
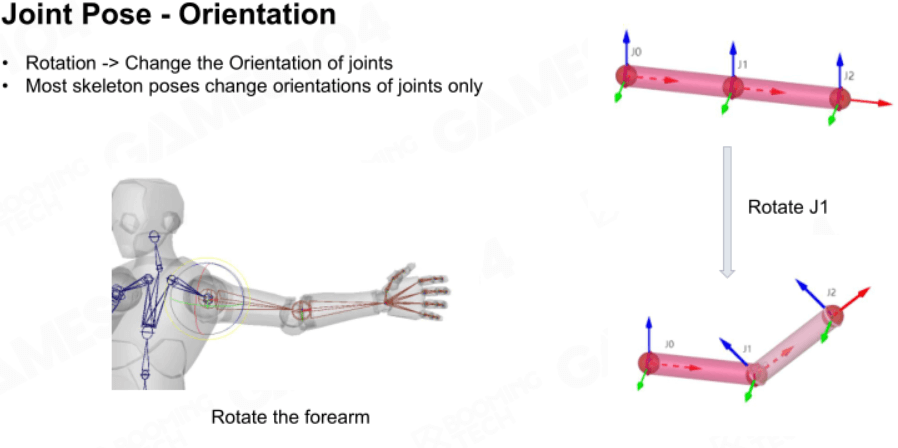
旋转
大量关节的运动主要以旋转为主,是动画表达的核心。
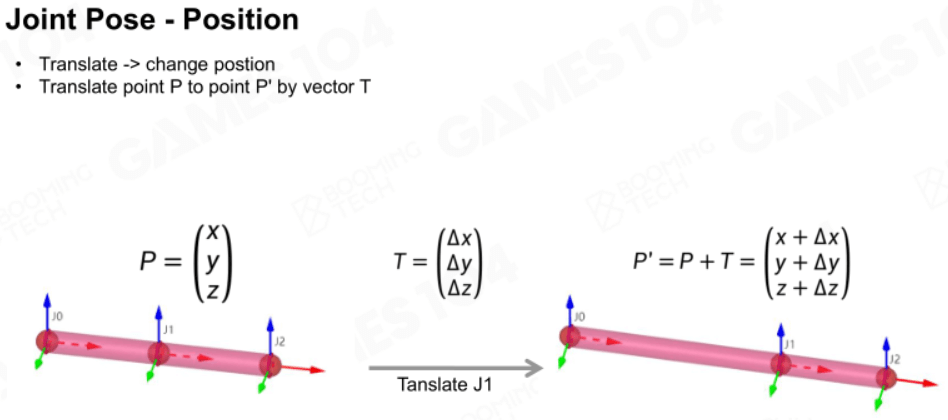
平移
在人的蹲起、表情变化、机械结构的变化动画中,需要对关节进行平移操作。

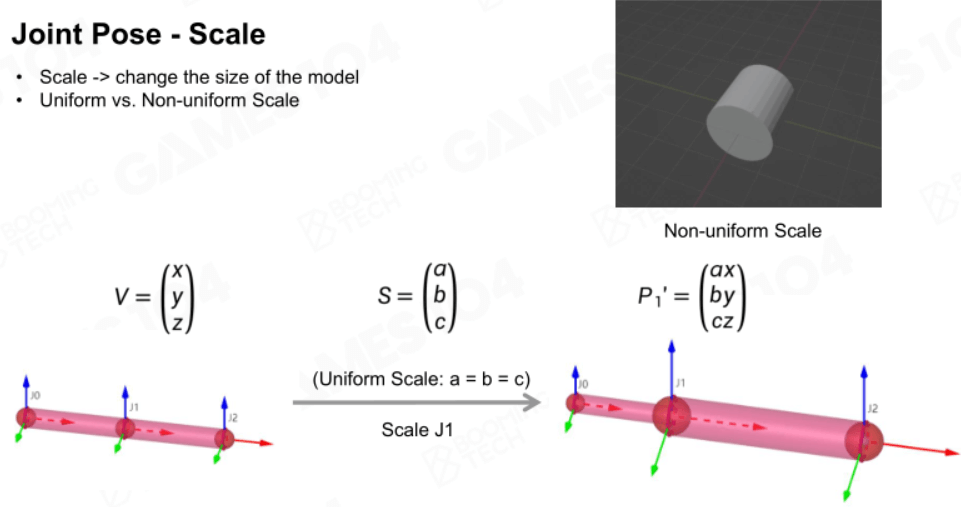
缩放
通常用于面部动画的表达。
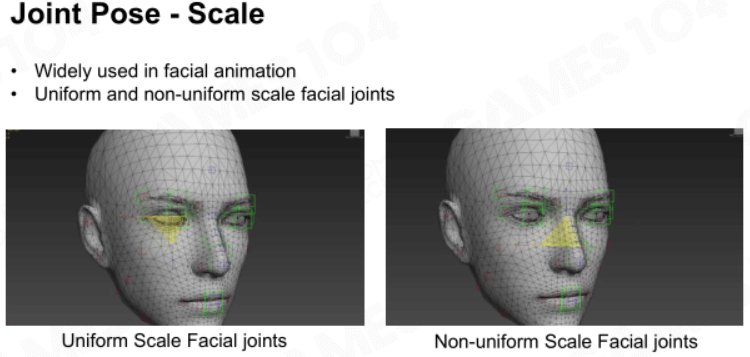
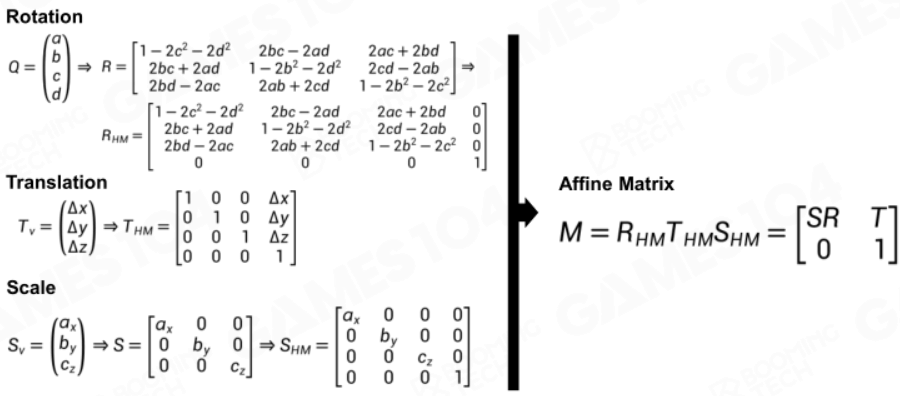
仿射矩阵
关节姿态的SRT变换可以整理成一个仿射矩阵:
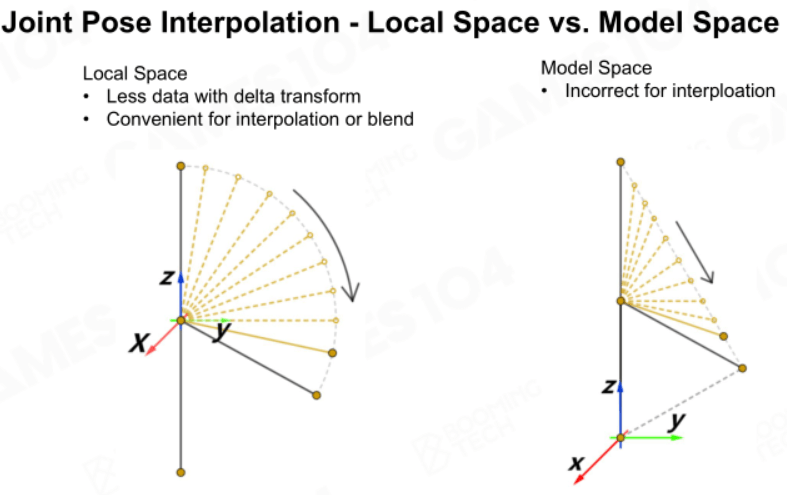
坐标系转换
关节相关数据需要存放在它自己的局部空间中,如果存放在模型空间中,会出现插值错误等问题。这和法线贴图的法线信息必须放在切线空间中一个道理。
对于蒙皮中的每一个关节,需要累积它和父节点直到根节点的仿射矩阵以得到它在模型空间的仿射矩阵:

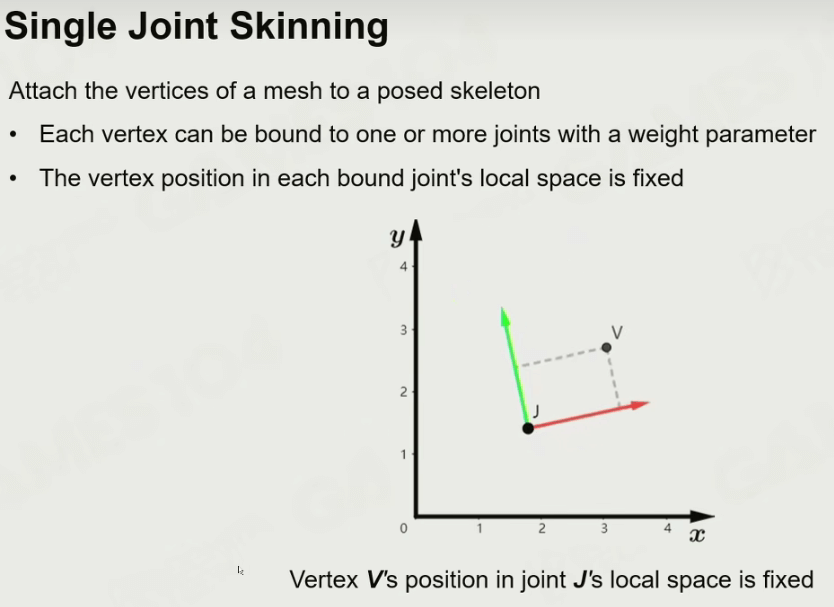
绑定网格顶点
有了关节的仿射矩阵,就能将模型上顶点和对应关节相关联,它们之间存在一种相对关系(例如距离是固定的)。
为了在数学上表示这种映射关系,需要蒙皮矩阵来帮忙,它先将初始状态顶点从模型空间变换到局部空间,再根据关节的累计仿射矩阵变换到模型空间,得到绑定好姿态的顶点。


为了减少不必要的蒙皮矩阵,需要预计算出每个关节对应姿势的蒙皮矩阵,在顶点计算时随用随取。此外由于顶点计算通常是在世界空间里,也能让蒙皮矩阵多左乘一个向世界空间变换的矩阵。

在内存中的表达方式
关节和骨架在内存中的表达方式如下,这里需要将关节仿射矩阵的逆矩阵存储下来,因为矩阵求逆也很麻烦。

蒙皮动画
多关节绑定
和单关节绑定类似,蒙皮动画是单顶点按权重绑定至多关节上。
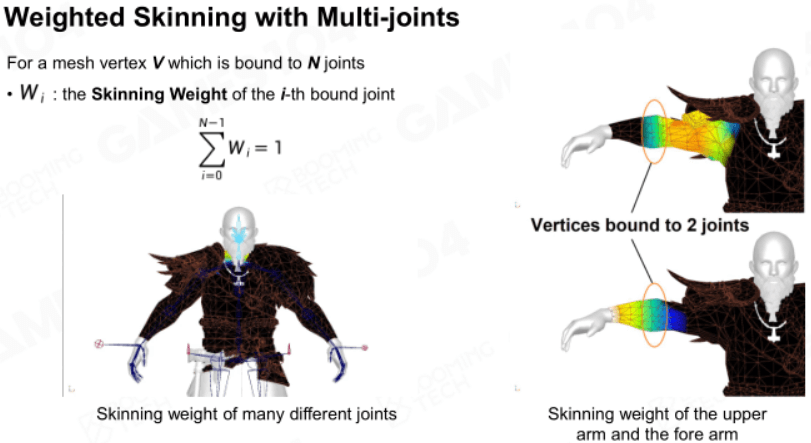
要计算该顶点经过绑定后的位置,需要在模型空间中按权重累积对应关节给它的变换。

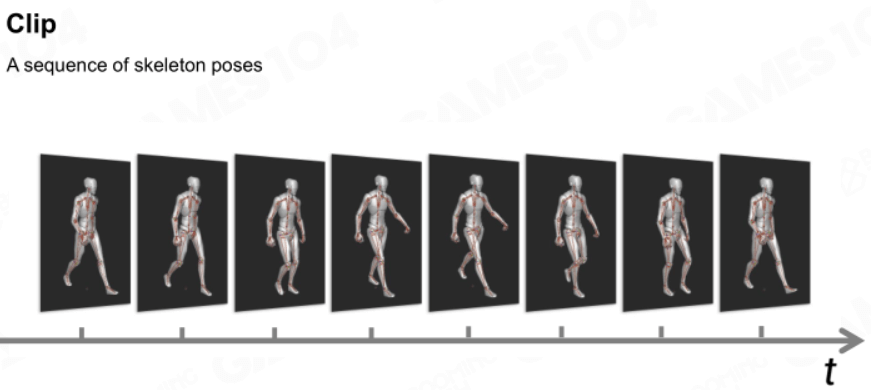
帧序列
一个帧序列就是骨架姿态随时间的组合。
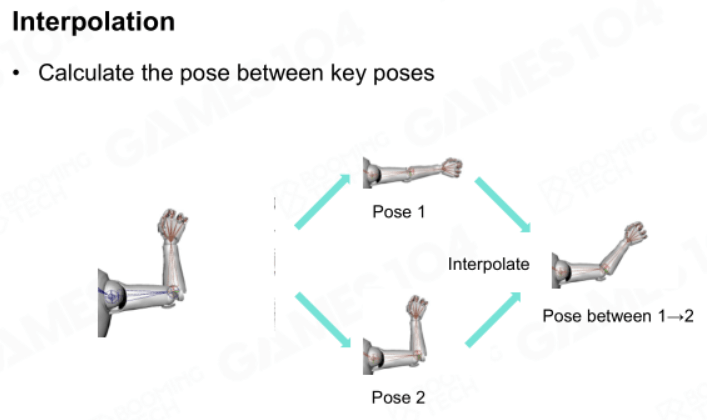
姿势间插值
由于只有关键帧的姿势,为了帧间姿势的平滑过渡,需要在姿势间进行插值。
线性插值LERP
对于位移和缩放变换,使用简单的线性插值即可:

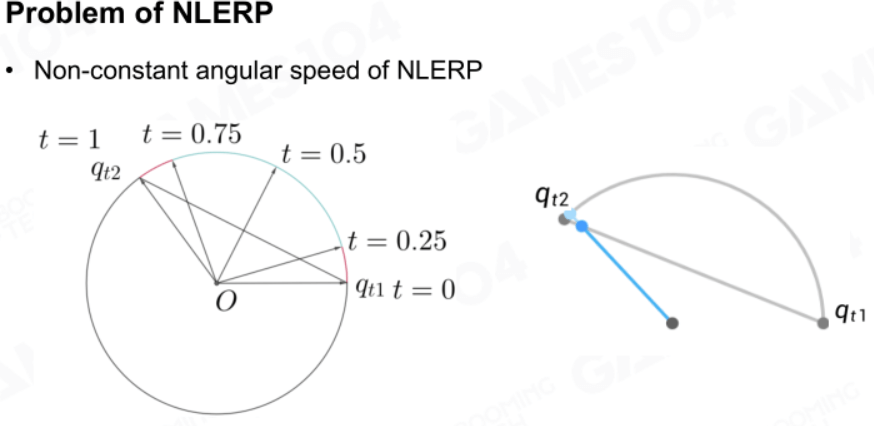
正规化线性插值NLERP
而旋转变换就有些特殊了,针对四元数要使用正规化线性插值NLERP或者球面线性插值SLERP,先看看NLERP。

有关NLERP需要注意的是,插值时要遵循最短路径原则,需要判断\(q_{t1}\cdot q_{t2}\)的大小,并根据大小决定插值的方向(顺逆时针)。如果不遵循最短路径原则,会在播放动画的时候出现关节突变的现象。

此外,NLERP还存在插值速度不均匀的问题,尤其是中间很快,两边较慢。
球面线性插值SLERP
SLERP的标准计算公式如下:
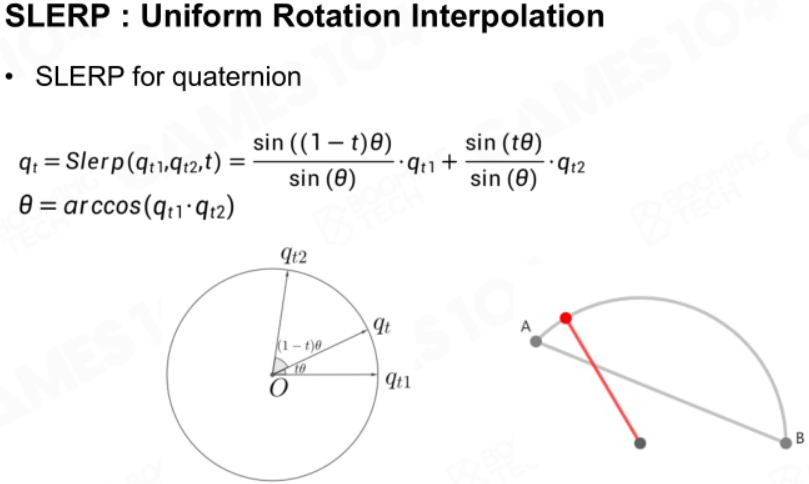
可以发现:当\(q_{t1}\,,q_{t2}\)非常接近,即\(\theta\)很小的时候,可能会导致除以0的问题。因此,在这种情况下要使用NLERP,其他情况下使用SLERP。
简单动画管线
上述内容可以总结成如下一张图,它描述了简单的动画管线:
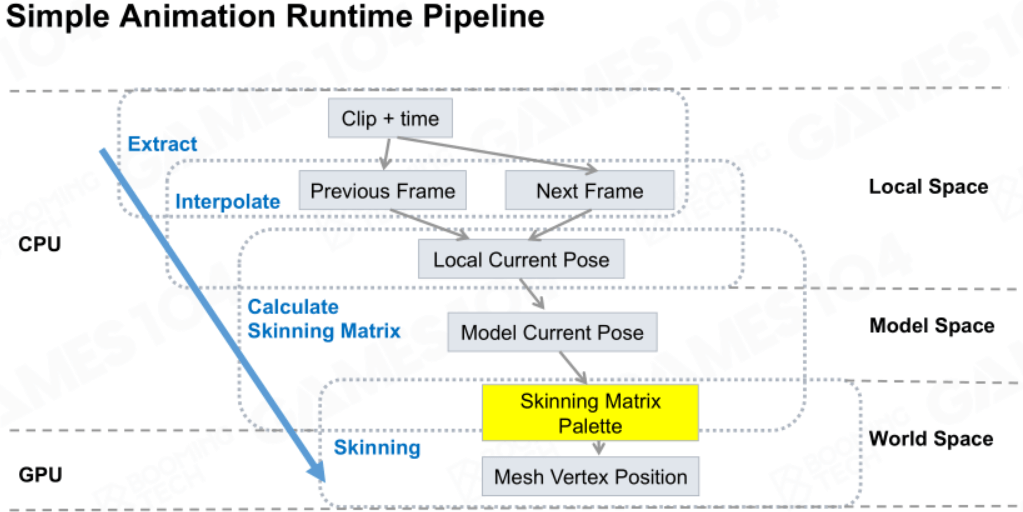
动画的压缩
原因
动画需要存储很多信息,例如单个帧序列需要存储如下信息:
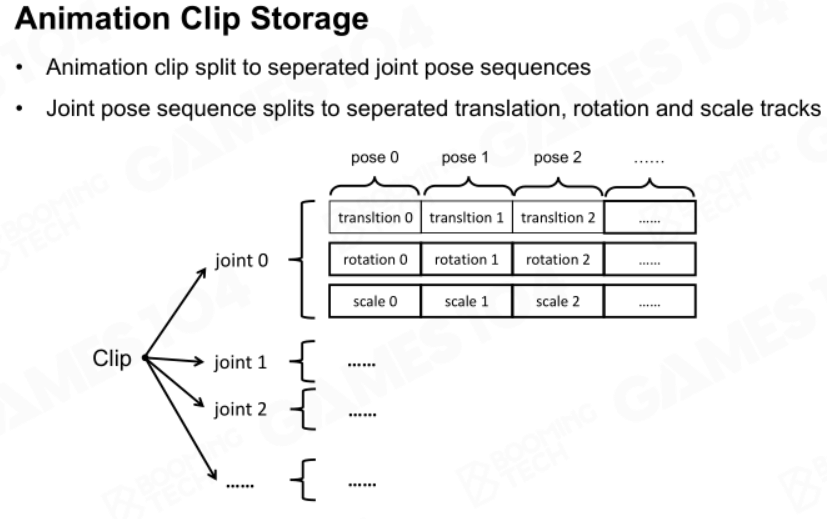
大小估算如下,可见消耗了较大空间:

因此需要对动画进行压缩。
做法
信息查重
看看一个关节所存储的SRT信息:
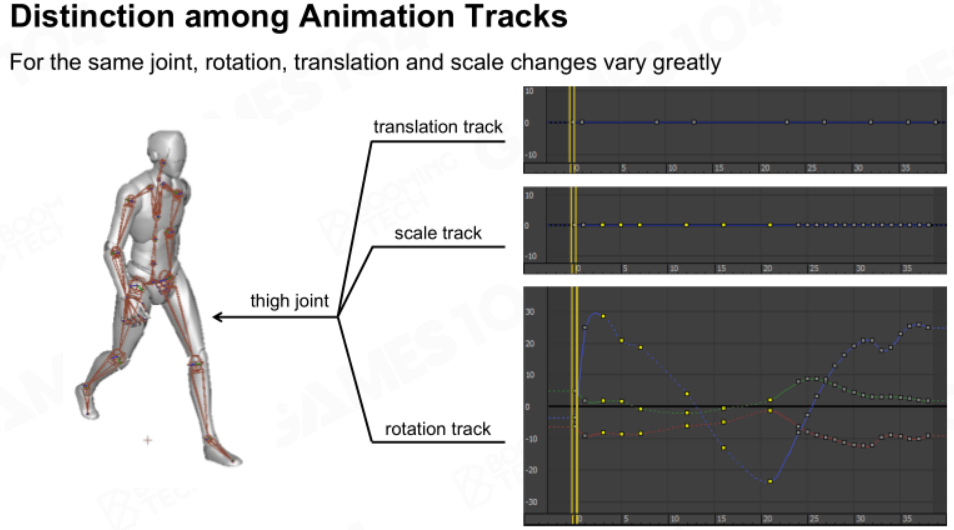
可以发现旋转R信息变化较大,平移T和缩放S几乎没有变化。因此可以忽略掉这些信息,只存储关节的旋转信息。
Ps:要保留面部关节SRT信息,以及尾椎骨等特殊关节的平移T信息。
使用关键帧
接下来在这些姿势信息中挑选一些关键的姿势,称为关键帧。然后其他时间的姿势可以通过在关键帧间插值实现。
线性关键帧插值
关键帧插值有许多算法,首先看看基于Marching思想的线性关键帧插值算法。它会在两个关键帧间尝试插值,如果容错率通过就返回当前插值结果;如果不通过则会尝试在两个“距离”更近的关键帧之间插值,直到容错率通过。
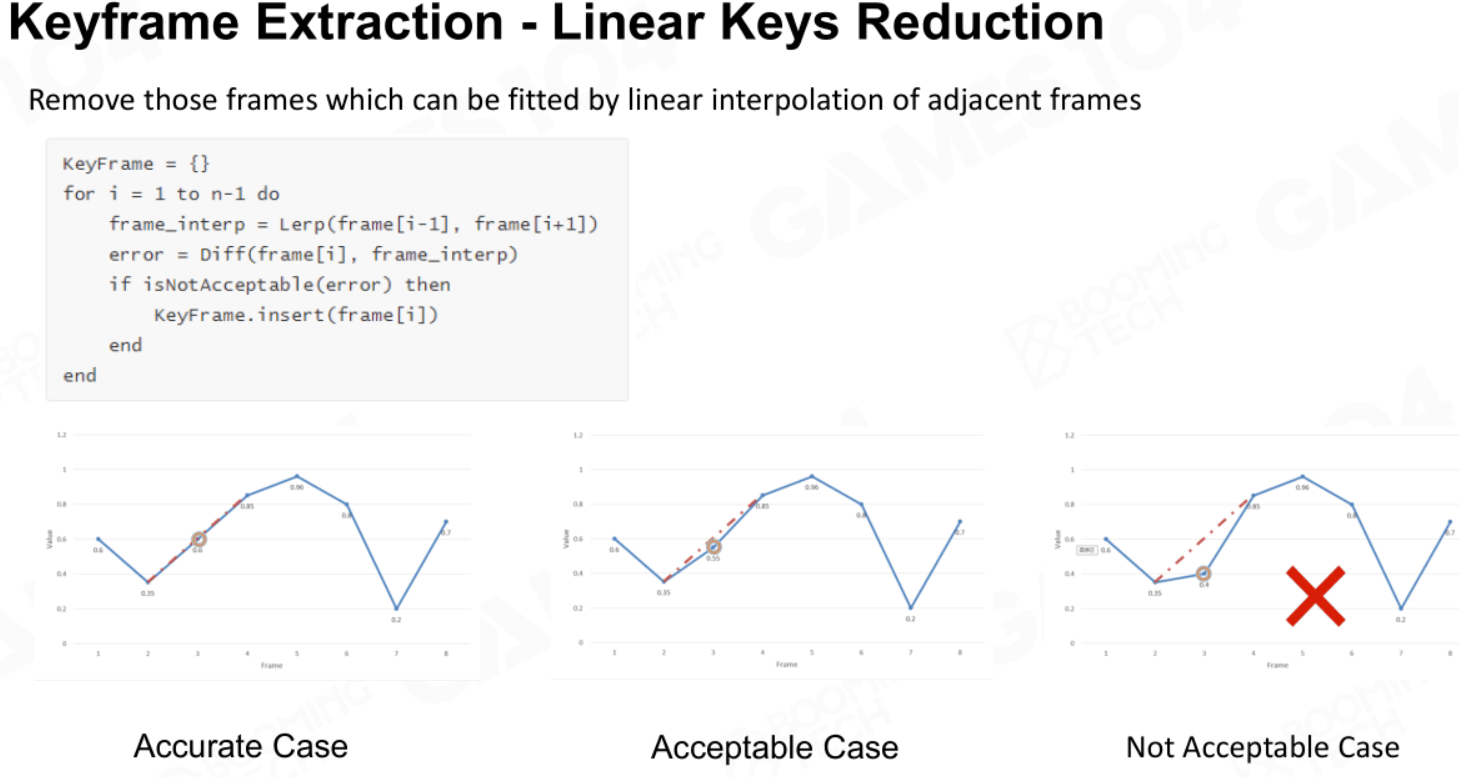
虽然计算简便,但这种差值方法对于关节的旋转变换来说还是有些生硬的。
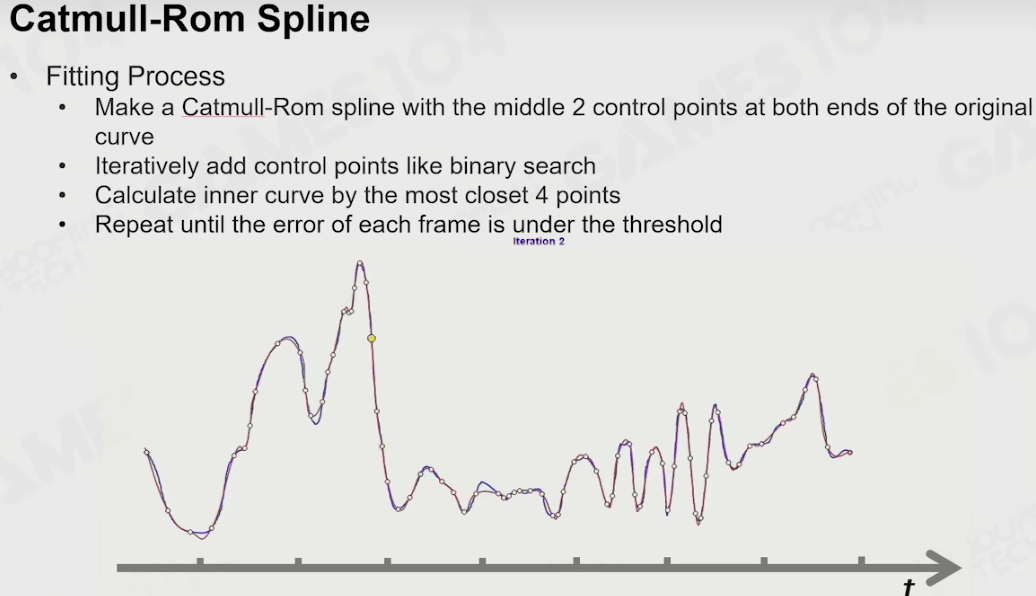
Catmull-Rom样条插值
为了让插值结果更光滑,可以使用Catmull-Rom样条曲线进行插值。其中\(\alpha\)是控制曲线锐度的参数,通常为0.5;它由4个控制点控制,最终会生成光滑曲线P1P2:

使用该样条曲线插值的过程如下:
定点数模拟
浮点数
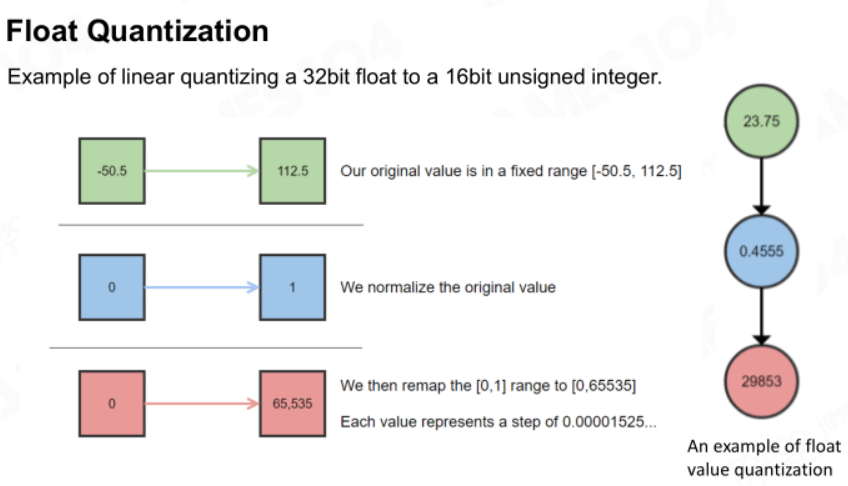
如果全部数据使用32位浮点数存储就太耗空间了,实际上可以使用位数更少的定点数来模拟这些浮点数。首先要根据公式去求定点数的位数,它的输入是要存储浮点数的范围和精度:

接下来就能将32位浮点数映射到定点数上了,下例将32位浮点数映射到16位无符号整数上。首先确定值域[-50.5, 112.5],然后将值域映射到[0, 1]上,最后再映射到整数上(16位无符号整数范围是[0, 65535])即可。右边的23.75则是更详细的例子。
四元数
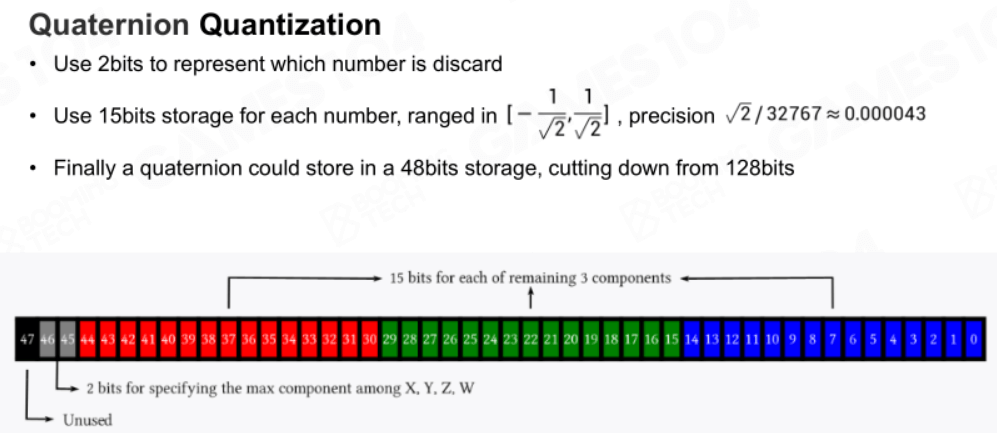
知道浮点数是怎么模拟后,就能用定点数来模拟四元数了。这里要用到单位四元数的特性,用三个数表达一个单位四元数,那么这三个数的范围一定位于\(\pm(1/\sqrt{2})\)之间。

那么一个四元数就能用48位来存储,而不是128位。其中1位保留;2位标识出用三个数表达出的第四个数是X,Y,Z,W中的哪一个;剩下45位中每15位各存储三个数中的一个数,使用定点数模拟浮点数。
综上,通过定点数模拟进行数据压缩可以极大减少存储空间。但也不可避免地带来一些精度问题,对于通过累乘计算仿射矩阵的关节来说,这种精度问题需要重视。
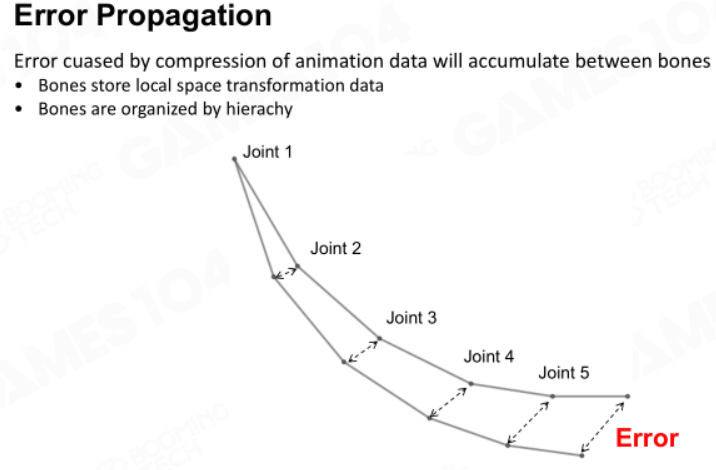
错误检测
数据的压缩会导致动画出现错误,这里以两种视角看一下如何发现错误。
数据视角
可以通过将插值数据和原始数据作比较,看看数据是否出错:

视觉视角
也可以在关节轴方向上放置两个垂直的假顶点,并给出一定偏移。然后用压缩前后的数据去测试观察,看看动画是否出错。

错误补偿
自适应错误容忍
为了避免父关节造成的错误影响自己,每个关节设定的错误容忍度都是不一样的。

就地纠正
在进行子关节的相关计算时,就地纠正父关节的误差&错误以进行错误补偿。

动画制作流程
建模
首先要构建Mesh模型,动画使用的是低精度模型。

使用低精度模型时,会在关节连接处添加一些额外的Mesh以增强表现力。
骨架绑定
然后要将人体基础骨架和建好的Mesh模型绑定。
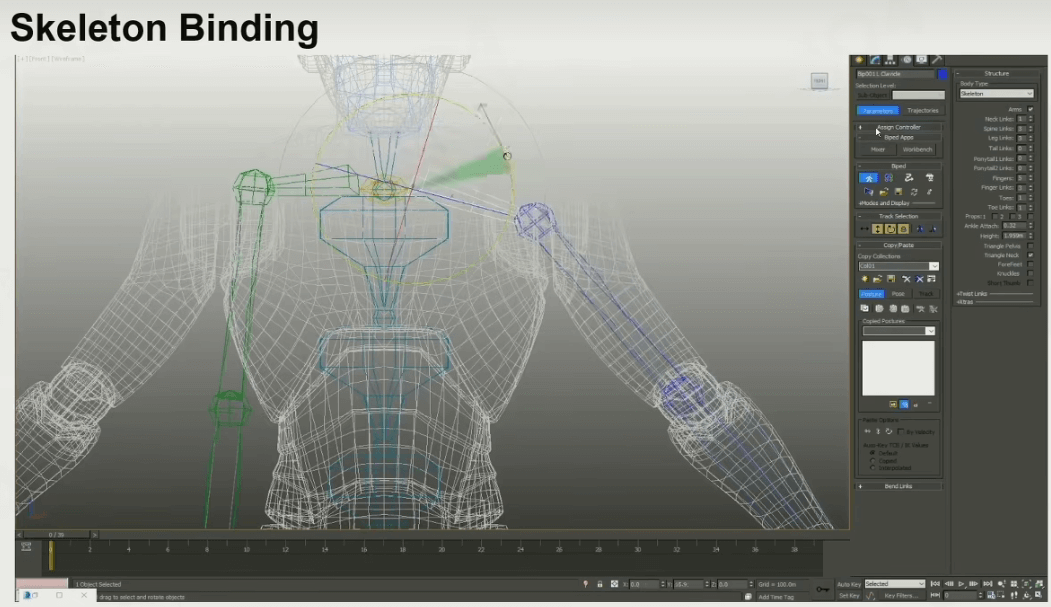
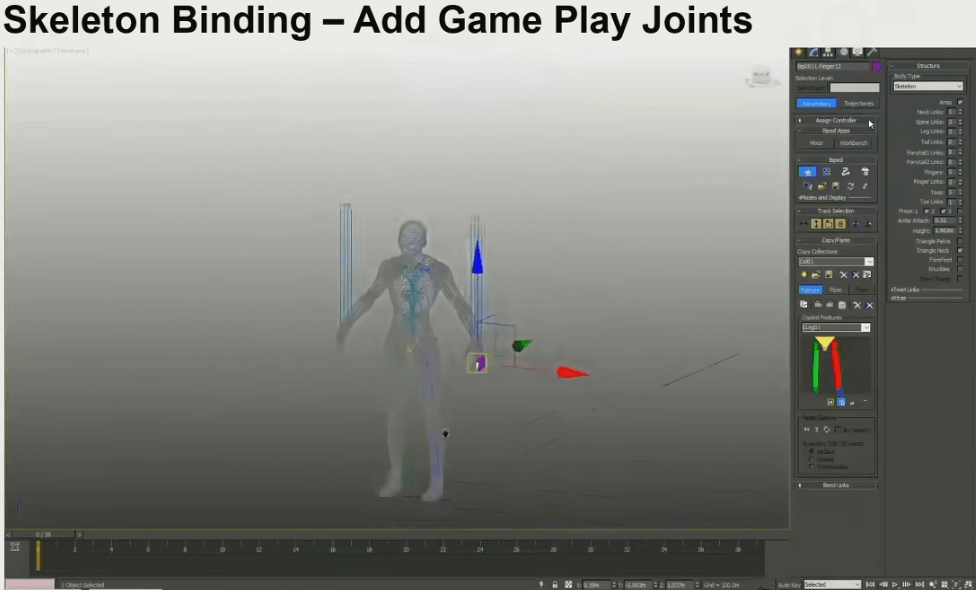
绑定好基础骨架后,可以选择性添加增强游戏性的额外骨架,例如手持武器的骨架。
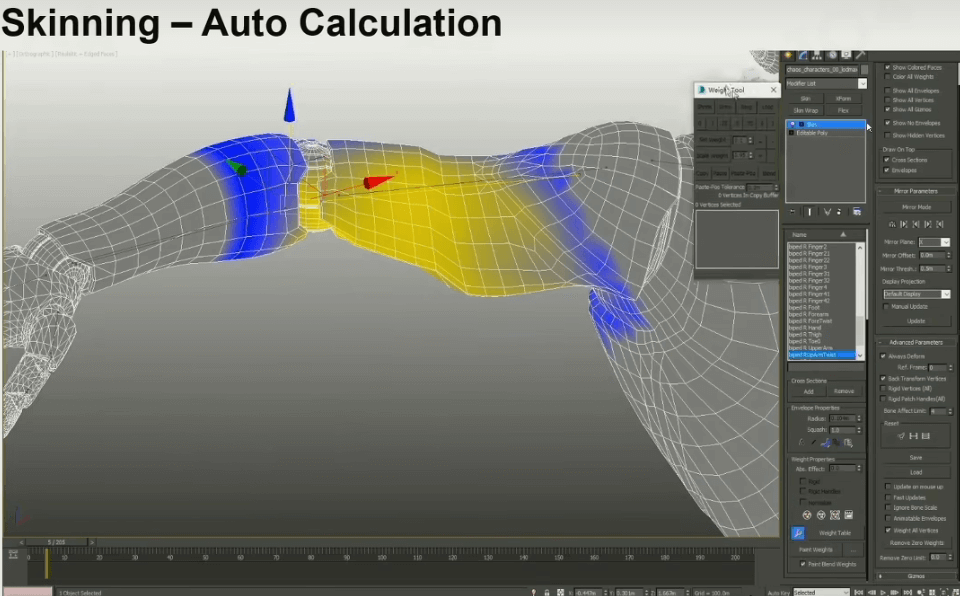
蒙皮
接下来需要进行蒙皮操作,可以先让软件自动计算一遍,然后艺术家再手调一下。
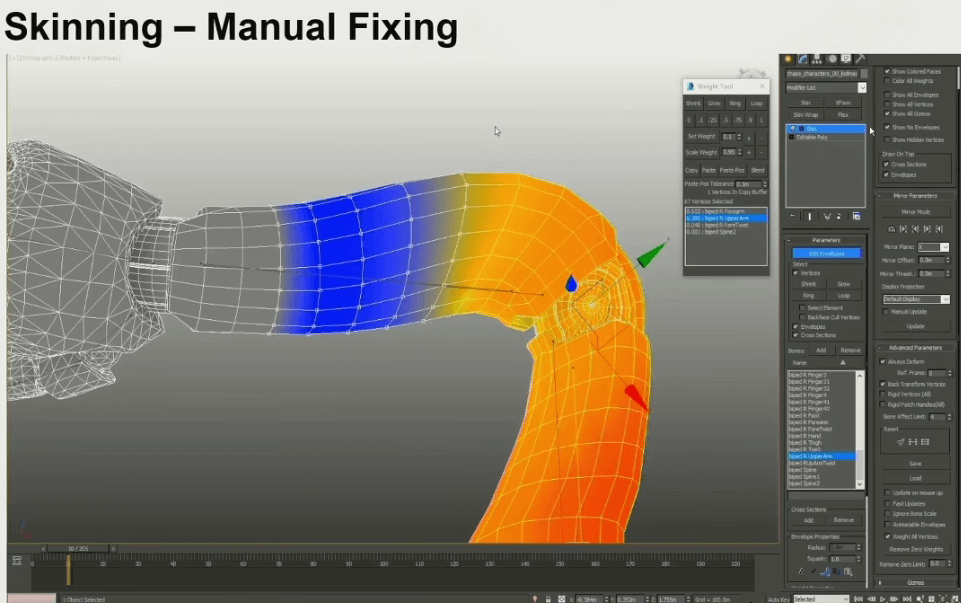
创建动画
接下来艺术家就要k帧去制作动画了。
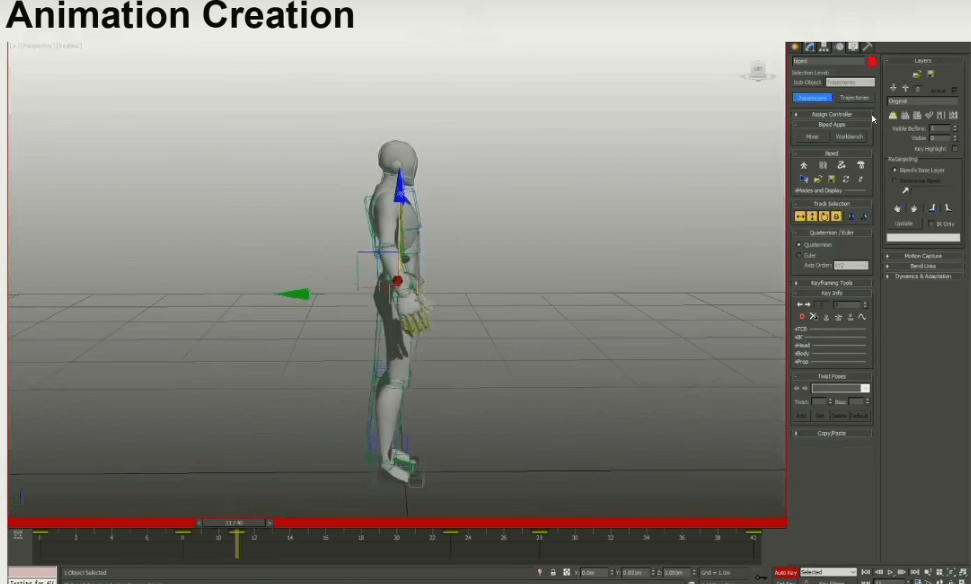
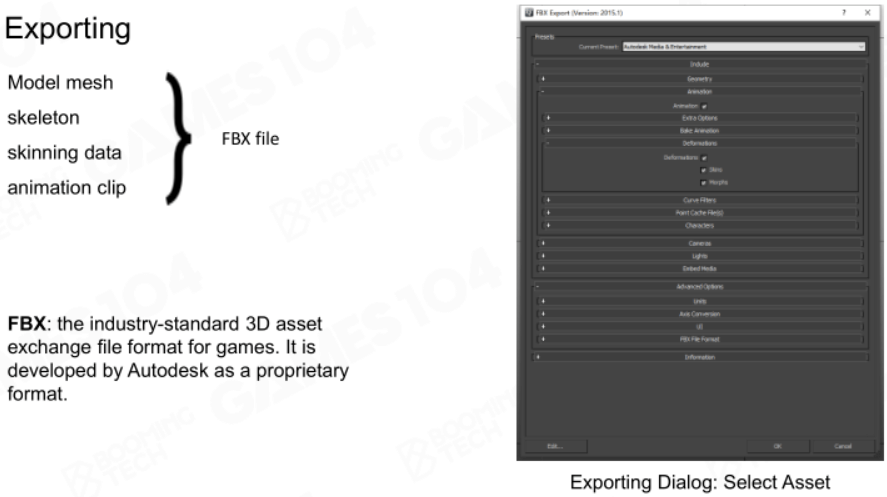
导出
最后就是要导出动画了,为了导出时动作统一,一般会将位移相关信息单独存储至曲线中,供游戏引擎使用。
参考资料
- GAMES104 (boomingtech.com)