6-简单IK

发表于 2024-11-26 更新于 2024-12-05 分类于图形API ， OpenGL ， 7-简单动画阅读次数： Waline：本文字数： 12k 阅读时长 ≈ 10 分钟

在看完GAMES104动画系统那一部分后，我也想写一个简单的动画系统，又要开一个坑了！本文将简要介绍如何实现简易的IK，包括：

Two Bones IK
CCD IK
FABRIK

简单IK

逆向运动学

在电子游戏中，逆向运动学(Inverse Kinematics)常用于让角色动作变得更自然，例如可以根据地形放置脚部。在机器人学中，IK被用于机械臂的移动，例如从目标点拿取一个物体。

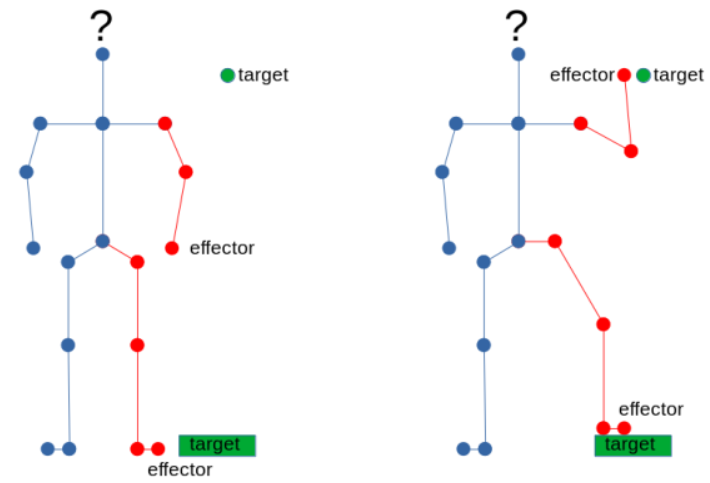
如图，在逆向运动学中，执行器 Effector 是骨架中的一部分，它应该到达 目标点 Target 。如果目标点距离执行器太远，执行器只需到达离目标点尽量近的位置即可。对于IK的求解有很多种方法，例如：

使用余弦定理求解两骨骼IK；
使用雅可比矩阵求解多骨骼IK；
使用启发式算法（CCD，FABRIK）求解多骨骼IK；

这里我们尝试简单实现1和3。

两骨骼IK

使用两骨骼IK（Two Bones IK）的前提条件如下：

骨骼的长度不变；
只有effector的父关节和根关节需要旋转。

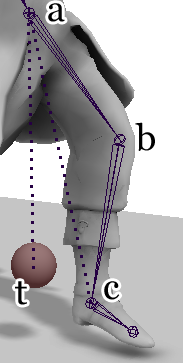
如图，C点就是Effector，T点就是Target，我们要想办法通过旋转关节A和B，尽量让C到达T。一共有两个步骤，首先需要旋转关节A和B，让AC的长度等于AT的长度；然后旋转关节A，让关节C到达点T。

第一步：伸展/收缩关节链

在这一步中，需要旋转关节A和B，让AC的长度等于AT的长度。

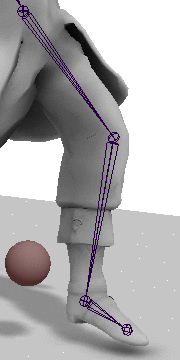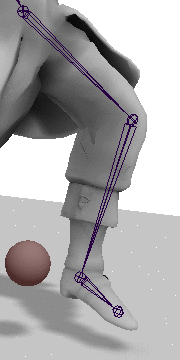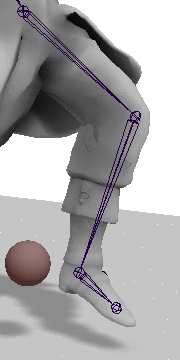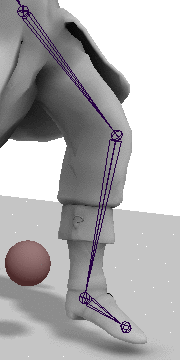
首先需要计算可达性，对AT可能的长度范围进行讨论： \[ \nonumber \begin{aligned}\max&=ab+bc\\\min&=\begin{cases}ab-bc,&ab>bc\\0&ab=bc\\bc-ab\end{cases}\\&=abs(ab-bc)\end{aligned} \\ 因此\quad |AT|=\mathrm{clamp}(|AT|,\, \min,\, \max) \] 这样便限制了AT的长度范围，如果AT的长度超出这个范围，就只能让C点去尽量靠近它了（就是使用最大值）。

接下来需要计算IK前的角\(\alpha_0\)和\(\beta_0\)：

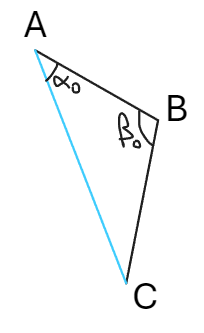
可由向量点乘得到这两个角的值： \[ \nonumber \angle\alpha_0 = \mathrm{acos}(\mathrm{normalized(}\overrightarrow{ac}) \cdot{\mathrm{normalized(}\overrightarrow{ab})})\\ \angle\beta_0 = \mathrm{acos}(\mathrm{normalized(}\overrightarrow{ba}) \cdot{\mathrm{normalized(}\overrightarrow{bc})})\\ \] 然后需要计算IK后的角\(\alpha_1\)和\(\beta_1\)：

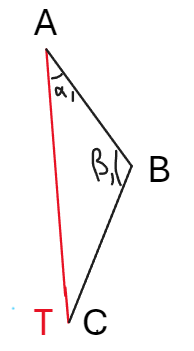
可通过余弦定理得到这两个角的值： \[ \nonumber \angle\alpha_{1}=\mathrm{acos}(\frac{|bc|^{2}-|ab|^{2}-|at|^{2}}{-2|ab|\cdot|at|})\\\angle\beta_{1}=\mathrm{acos}(\frac{|at|^{2}-|ab|^{2}-|bc|^{2}}{-2|ab|\cdot|bc|}) \] 那么两关节A，B的旋转角度就是： \[ \nonumber \angle\alpha=\angle\alpha_1-\angle\alpha_0 \\ \angle\beta=\angle\beta_1-\angle\beta_0 \\ \] 有了旋转角后还需要一个旋转轴\(\mathbf{AC}\times \mathbf{AB}\)，然后就能旋转关节A和B了。但如果在骨骼伸直的情况（即AC和AB接近一条直线）下，上述计算结果会不稳定，因此可以引入一个向量\(\mathbf{D}\)来代替向量\(\mathbf{AB}\)，它应该尽量和向量\(\mathbf{AC}\)垂直，通常被设置为膝盖指向的方向。

第二步：旋转A关节，让Effector到达Target

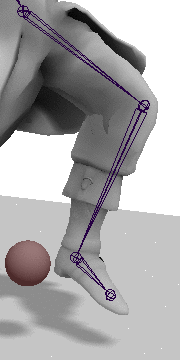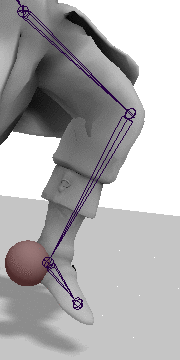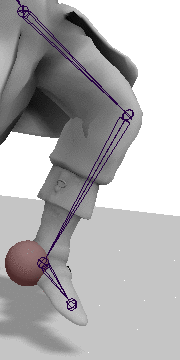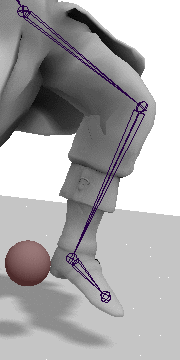
接下来需要旋转A关节，让Effector到达target，其中：

旋转角是\(\mathrm{acos}(\frac{\overrightarrow{ac}}{|\overrightarrow{ac}|}\cdot\frac{\overrightarrow{at}}{|\overrightarrow{at}|})\).
旋转轴是\(\mathbf{AC}\times \mathbf{AT}\)。

接下来是算法的代码实现，其中rootPos是A关节的世界坐标，middlePos是B关节的世界坐标，effectorPos是C关节的世界坐标，：

// AnimTwoBoneIKSolver.hpp
static void SolveTwoBoneIK(glm::vec3 rootPos, glm::vec3 middlePos, glm::vec3 effectorPos,
						   glm::vec3 targetPos,
						   glm::quat rootGlobalRotation, glm::quat middleGlobalRotation,
						   glm::quat& rootLocalRotation, glm::quat& middleLocalRotation,
						   float eps = 0.0001f)
{
	glm::vec3 ab = middlePos - rootPos;
	glm::vec3 ac = effectorPos - rootPos;
	glm::vec3 at = targetPos - rootPos;
	glm::vec3 cb = middlePos - effectorPos;

	// Step1: 旋转关节root和middle, 让dist(root, effector) == dist(root, target)
	float len_ab = glm::length(ab);
	float len_cb = glm::length(cb);
	// 计算可达性
	float len_at = glm::clamp(glm::length(at), eps, len_ab + len_cb + eps);
	// 计算Step1中, 关节root和middle的旋转角
	float angle_ac_ab_0 = std::acos(std::clamp(glm::dot(glm::normalize(ac), glm::normalize(ab)),
											   -1.f, 1.f));
	float angle_ba_bc_0 = std::acos(std::clamp(glm::dot(glm::normalize(-ab), glm::normalize(-cb)),
											   -1.f, 1.f));
	float angle_ac_ab_1 = std::acos(std::clamp(static_cast<float>(
		(len_cb * len_cb - len_ab * len_ab - len_at * len_at) / (-2.0 * len_ab * len_at)),
		-1.f, 1.f));
	float angle_ba_bc_1 = std::acos(std::clamp(static_cast<float>(
		(len_at * len_at - len_ab * len_ab - len_cb * len_cb) / (-2.0 * len_ab * len_cb)),
		-1.f, 1.f));
	float angle_ac_ab = angle_ac_ab_1 - angle_ac_ab_0;
	float angle_ba_bc = angle_ba_bc_1 - angle_ba_bc_0;
	// 计算Step1中, 关节root和middle的旋转轴
	glm::vec3 d = glm::rotate(middleGlobalRotation, glm::vec3(0, 0, 1));
	glm::vec3 axis0 = glm::normalize(glm::cross(ac, d));
	// 旋转关节root和middle, 注意旋转轴"世界空间->模型本地空间"的转换
	rootLocalRotation = glm::rotate(rootLocalRotation, angle_ac_ab, axis0 * glm::inverse(rootGlobalRotation));
	middleLocalRotation = glm::rotate(middleLocalRotation, angle_ba_bc, axis0 * glm::inverse(rootGlobalRotation));

	// Step2: 旋转root关节, 让Effector到达Target
	float angle_ac_at = std::acos(std::clamp(glm::dot(glm::normalize(ac), glm::normalize(at)),
											 -1.f, 1.f));
	glm::vec3 axis1 = glm::normalize(glm::cross(ac, at));
	rootLocalRotation = glm::rotate(rootLocalRotation, angle_ac_at, axis1 * glm::inverse(rootGlobalRotation));
}

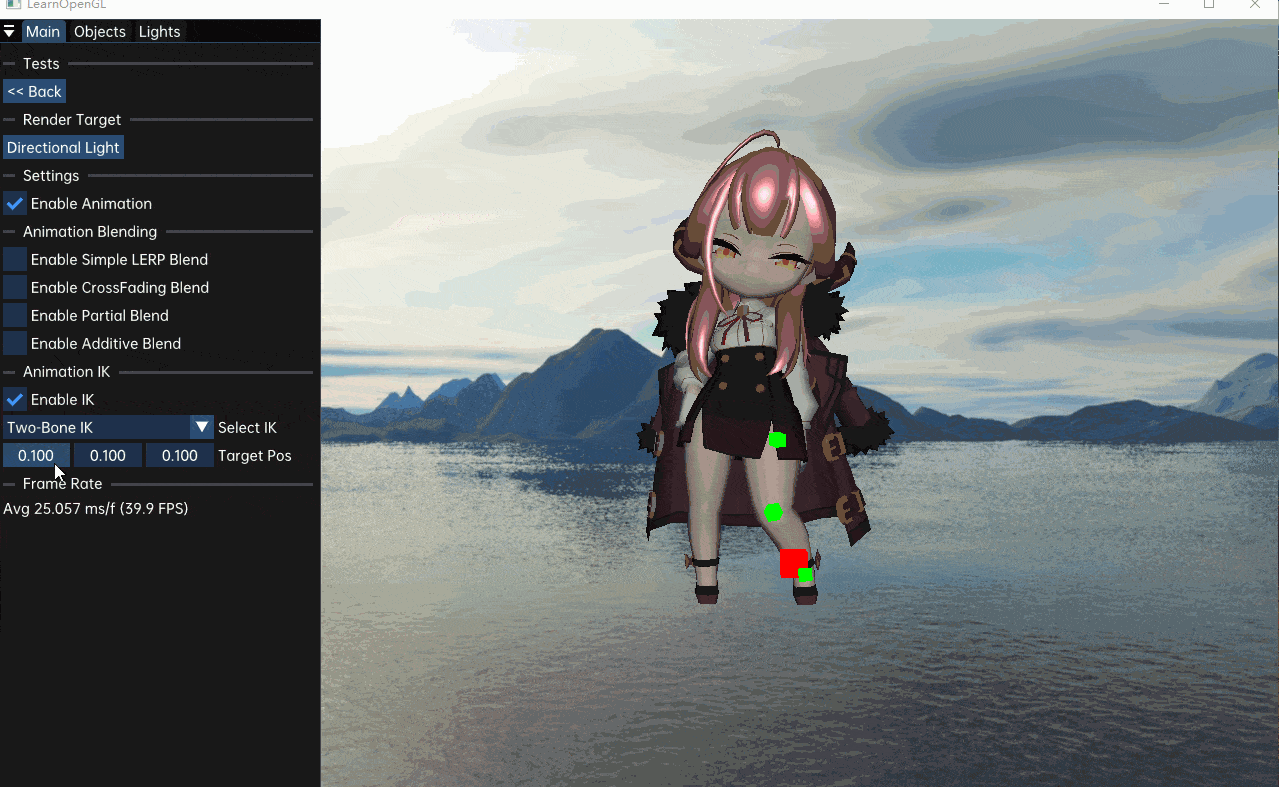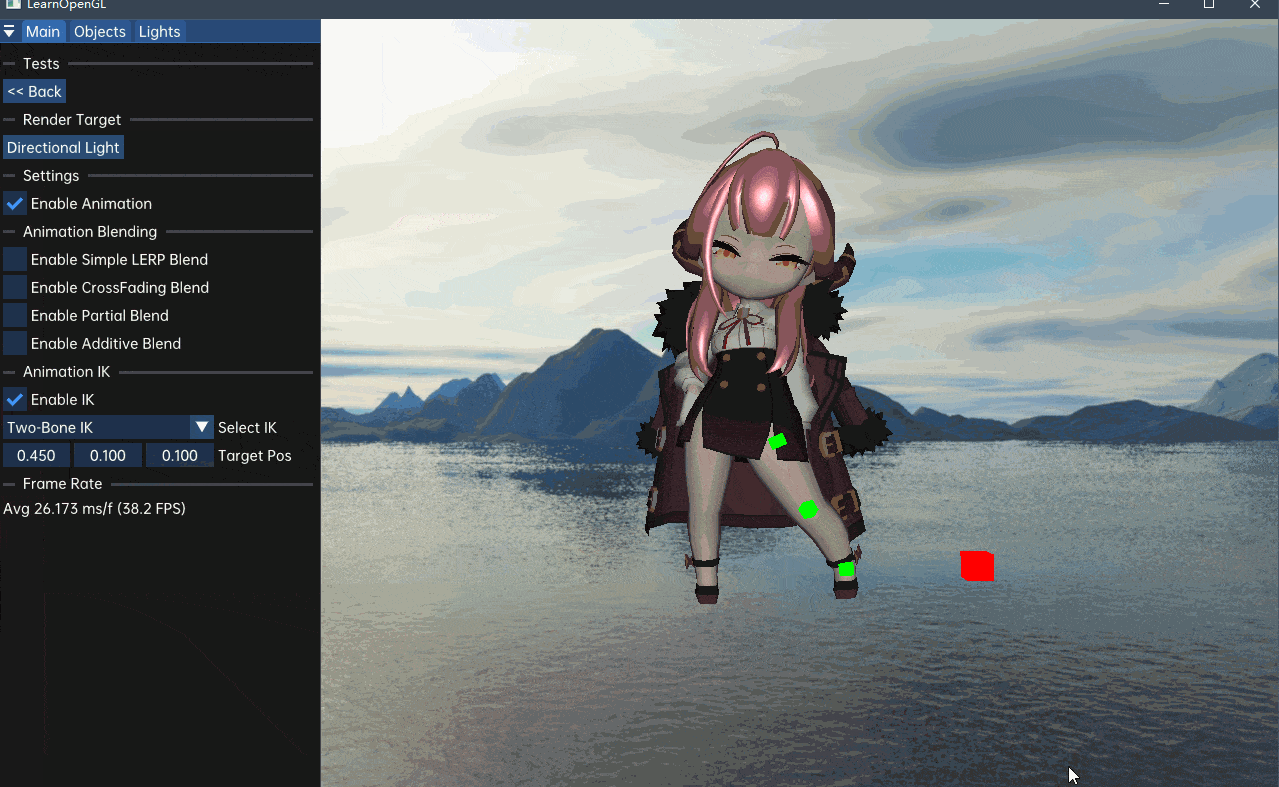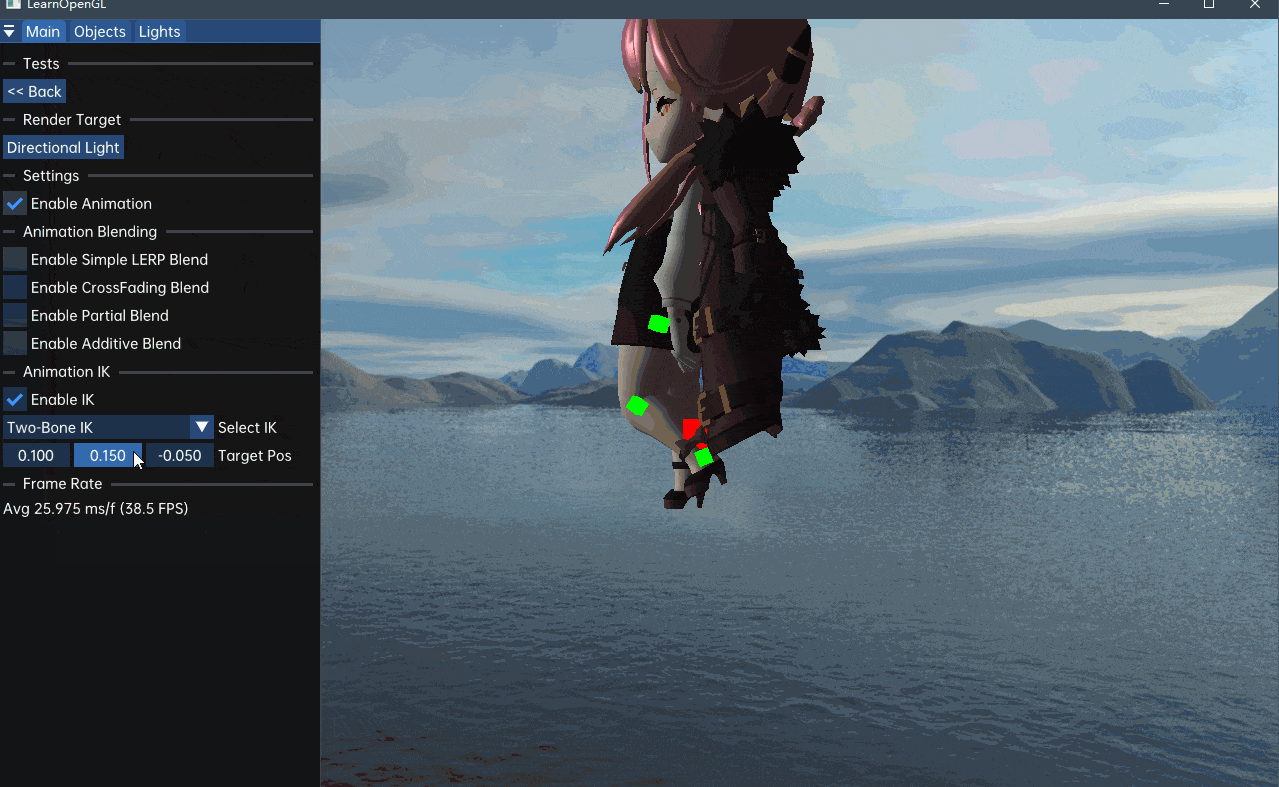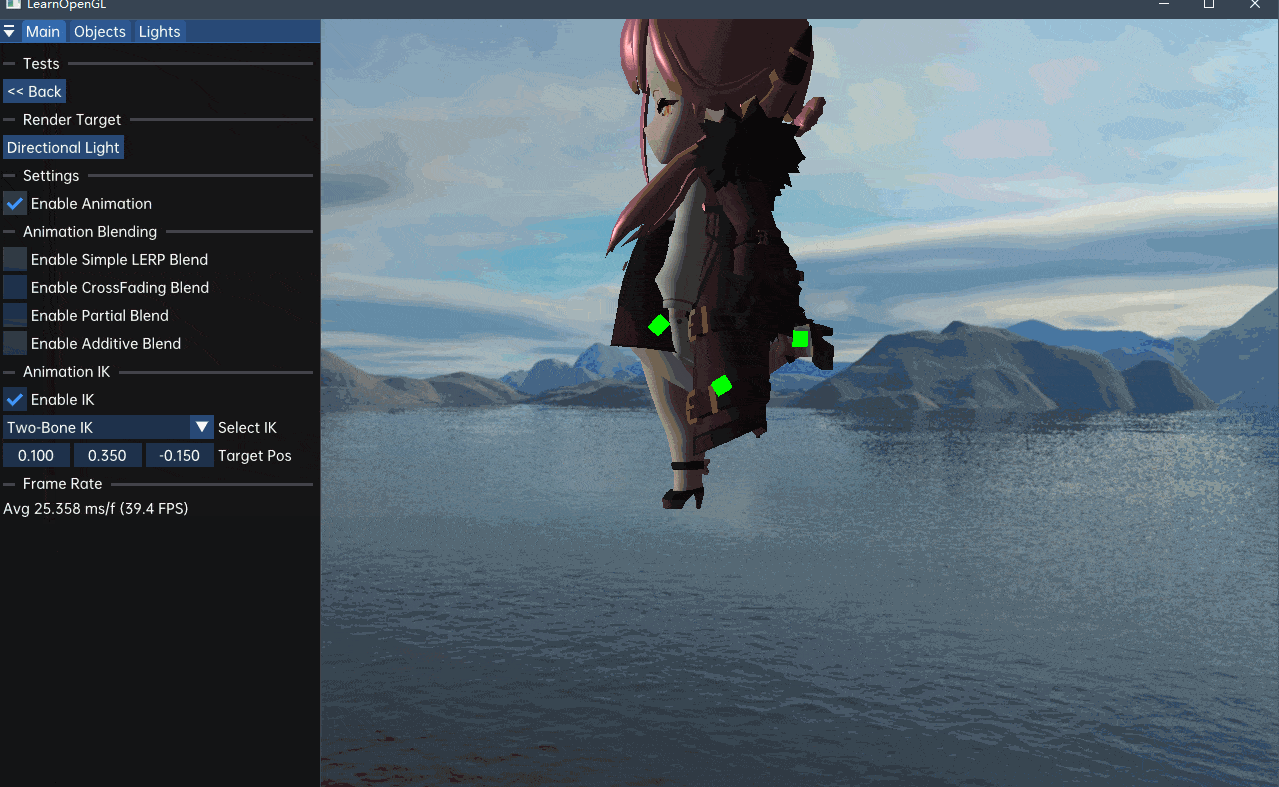
可以发现效果还算不错，但我觉得可能有写错的地方，有时间再看看吧。接下来看看解决多骨骼IK的启发式算法，CCD和FABRIK。

循环坐标下降法CCD

首先看看CCD算法的思路。CCD的基本思想就是用迭代的方式旋转每根骨骼，让Effector尽量靠近Target。接下来看看它的一次迭代过程：

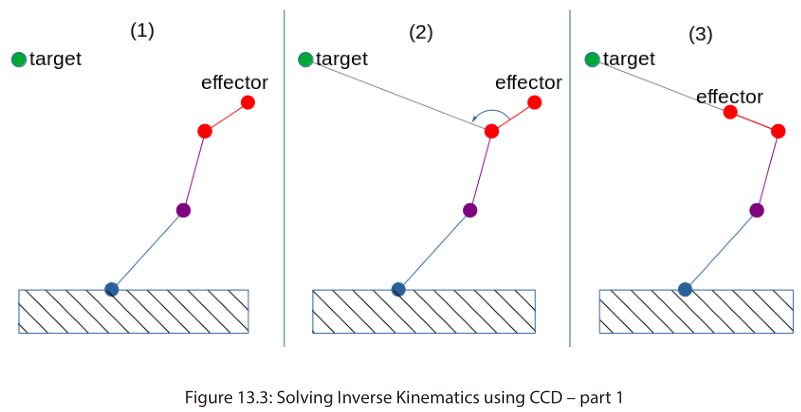
可以看到这张图里有3根骨骼，1个Target点和一个Effector点。
接下来把Effector点的下一个点和Target点连线，这条连线就是Effector点的下一个点和Target点的最短矩。
现在需要旋转这个点，让Effector点和这条连线相接。
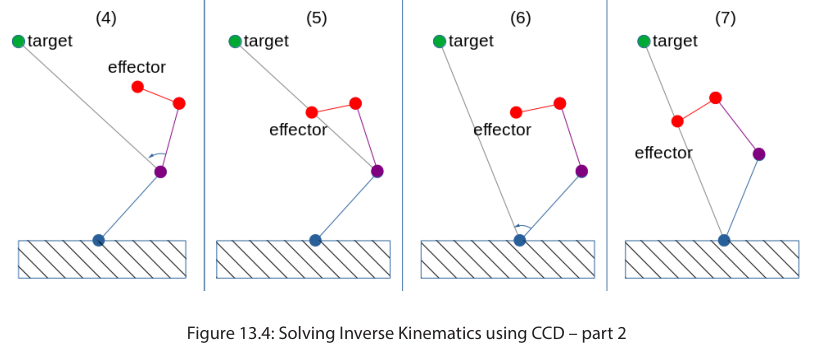
将Target和紫色点连线。
旋转紫色点，让Effector点和这条连线相接。
将Target和蓝色点连线。
旋转蓝色点，让Effector点和这条连线相接。

这样第一次CCD迭代便结束了。如果Effector点还未和Target点尽量接触，就会进行下一轮迭代，直到Effector点到达Target点/迭代次数达到上限。

CCD算法的动图如下：

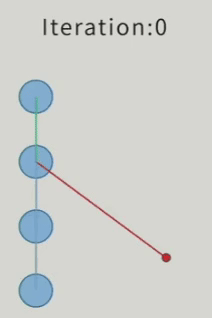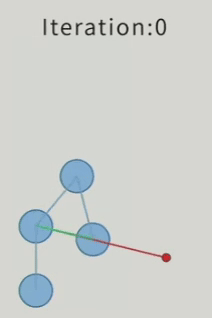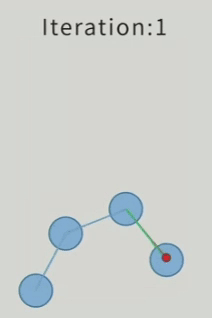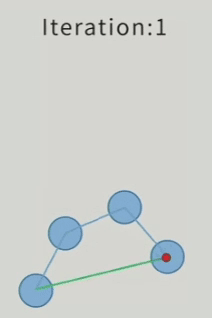
接下来尝试实现简单CCD算法，代码如下（这段写的不怎么好，有时间优化优化）：

// Animator.cpp
else if (m_animIKOpt == 2 && CheckIkParam())
{
    m_isCalcIk = true;

    // 准备IK需要的参数
    auto boneIDMap = m_currentAnimation->GetBoneIDMap();
    std::vector<glm::quat> vNodeGlobalRotation;
    for (size_t i = 0; i < m_ikChainParam.vpNodeList.size(); ++i)
    {
        AssimpNodeData* pCurNode = m_ikChainParam.vpNodeList.at(i);
        Bone* pCurBone = m_currentAnimation->FindBone(pCurNode->name);
        BoneInfo curBoneInfo = boneIDMap[pCurNode->name];

        glm::quat globalRotation = AnimBlendHelper::GetRotationFromMat4(m_finalBoneMatrices[curBoneInfo.id] *
                                                                        curBoneInfo.offset);
        glm::quat localRotation = pCurBone->GetCurOrientation();
        vNodeGlobalRotation.emplace_back(globalRotation);
    }

    // 进行CCD IK
    // TODO: 看看能不能封装到SolveCCDIK函数里, 估计不行了...
    const float CCD_THRESHOLD = 0.00001f;
    for (int i = 0; i < m_ikIterationCnt; ++i)
    {
        // 符合条件就提前结束
        if (glm::length(m_ikChainParam.targetWorldPos - m_ikChainParam.vNodeWorldPosList.at(0)) <= CCD_THRESHOLD)
        {
            break;
        }

        // 从Effector的下一个节点开始遍历
        for (int j = 1; j < m_ikChainParam.vpNodeList.size(); ++j)
        {
            AssimpNodeData* pCurNode = m_ikChainParam.vpNodeList.at(j);
            Bone* pCurBone = m_currentAnimation->FindBone(pCurNode->name);
            BoneInfo curBoneInfo = boneIDMap[pCurNode->name];

            glm::vec3 curWorldPos = m_ikChainParam.vNodeWorldPosList.at(j);
            glm::quat curGlobalRotation = vNodeGlobalRotation.at(j);

            // 计算Global坐标系下的旋转变换量
            glm::vec3 toEffector = glm::normalize(m_ikChainParam.vNodeWorldPosList.at(0) - curWorldPos);
            glm::vec3 toTarget = glm::normalize(m_ikChainParam.targetWorldPos - curWorldPos);
            glm::quat effectorToTarget = glm::normalize(glm::rotation(toEffector, toTarget));

            // 获取Local坐标系下的旋转变换量
            glm::quat localRotation = curGlobalRotation * effectorToTarget * glm::conjugate(curGlobalRotation);
            localRotation = glm::normalize(localRotation);

            // 在Local坐标系下旋转当前节点
            glm::quat currentRotation = glm::normalize(pCurBone->GetCurOrientation() * localRotation);
            pCurBone->SetCurOrientation(currentRotation);
            pCurBone->SetLocalTransformByCurSRT();

            // 更新矩阵
            glm::mat4 parentTransform = glm::mat4(1.0f);
            AssimpNodeData* pParentNode = pCurNode->pParentNode;
            if (pParentNode != nullptr)
            {
                BoneInfo rootParentBoneInfo = boneIDMap[pParentNode->name];
                parentTransform = m_finalBoneMatrices[rootParentBoneInfo.id] * glm::inverse(rootParentBoneInfo.offset);
            }
            CalculateBoneTransform(m_currentAnimation, pCurNode, m_currentTime, parentTransform);

            // 更新世界坐标
            for (int k = j - 1; k >= 0; --k)
            {
                AssimpNodeData* pTmpNode = m_ikChainParam.vpNodeList.at(k);
                BoneInfo tmpBoneInfo = boneIDMap[pTmpNode->name];
                glm::mat4 tmpModelMat = m_ikChainParam.objModelMat *
                    m_finalBoneMatrices[tmpBoneInfo.id] * glm::inverse(tmpBoneInfo.offset);
                m_ikChainParam.vNodeWorldPosList.at(k) = tmpModelMat[3];
            }

            // 符合条件就提前结束
            if (glm::length(m_ikChainParam.targetWorldPos - m_ikChainParam.vNodeWorldPosList.at(0)) <= CCD_THRESHOLD)
            {
                break;
            }
        }
    }

    m_isCalcIk = false;
}

效果如下：

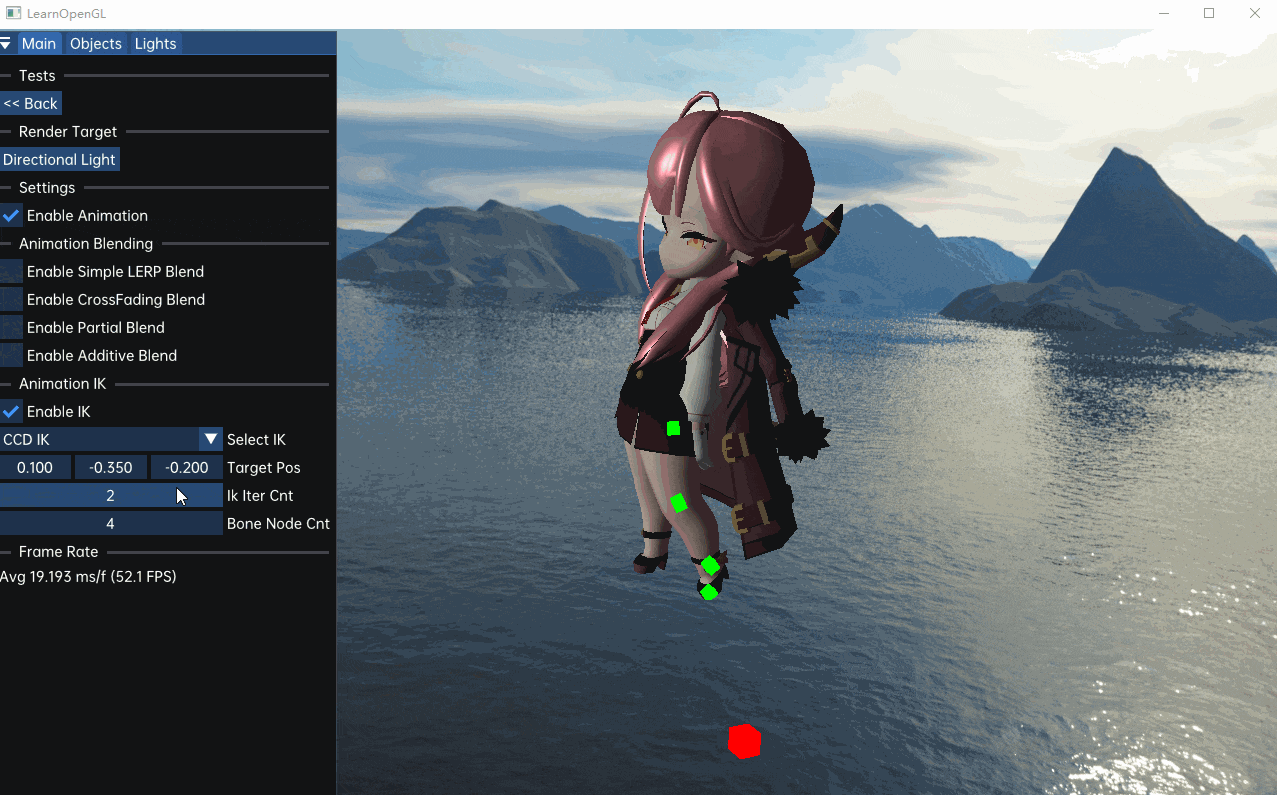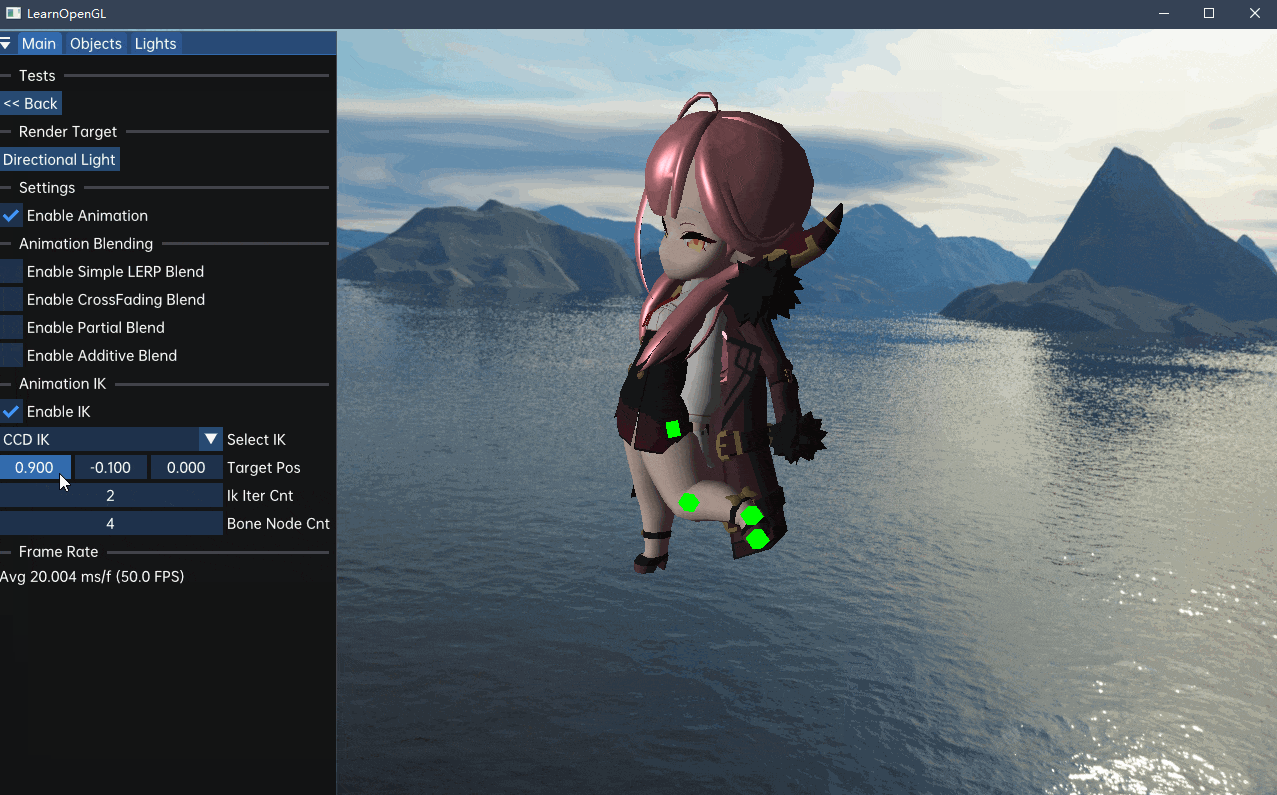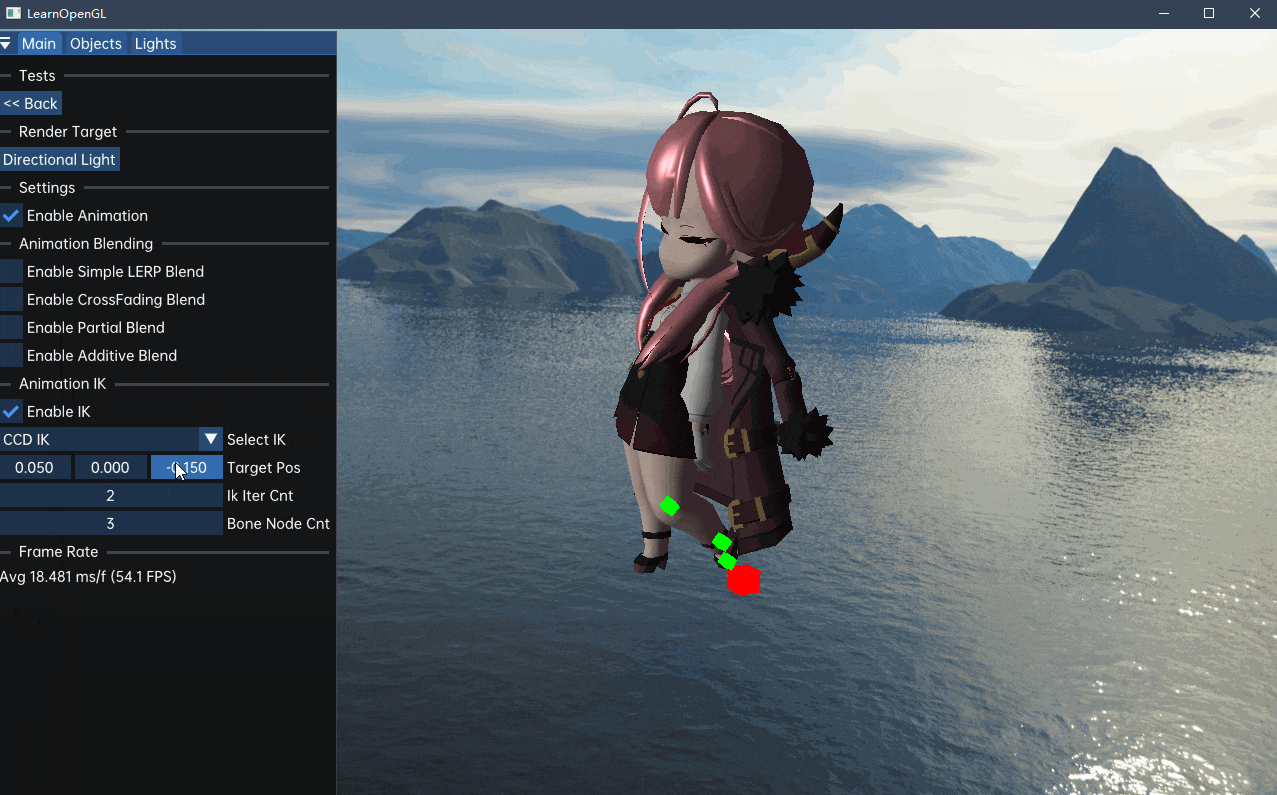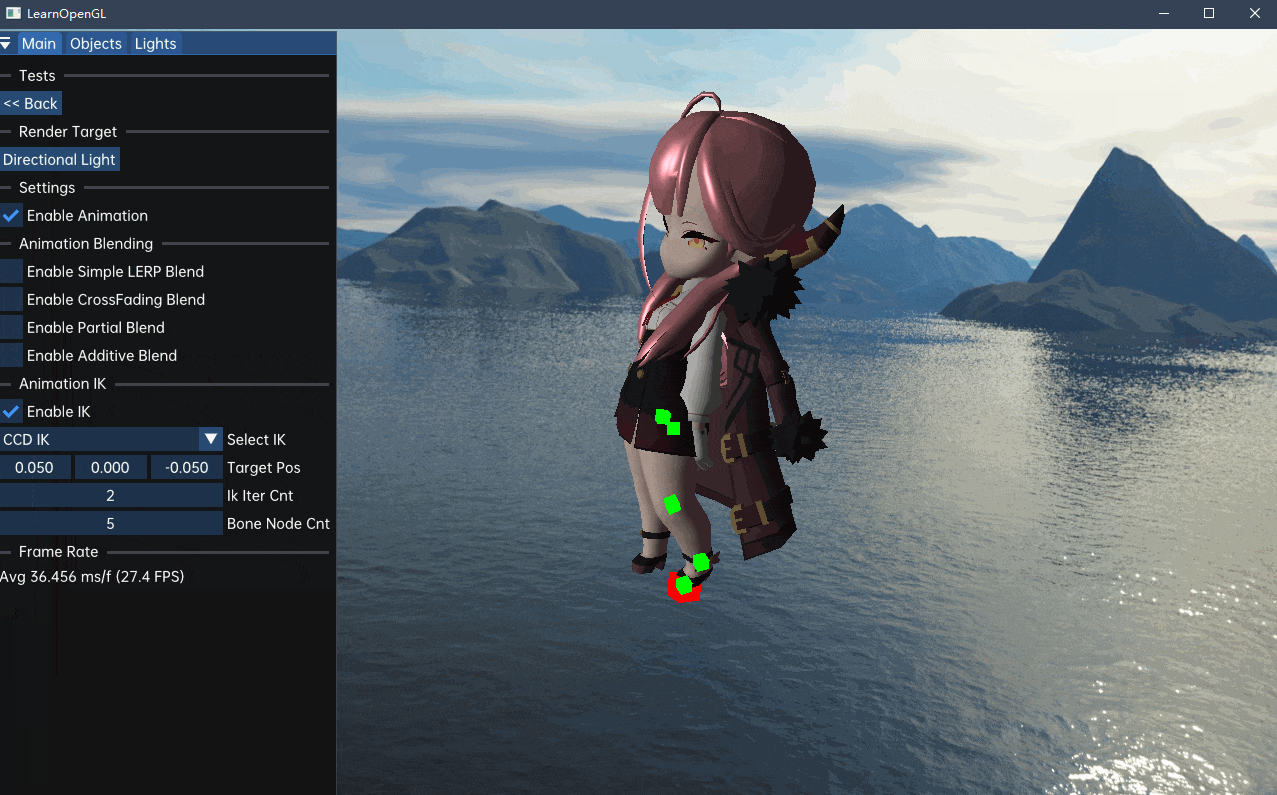
使用纯CCD方法可能会出现骨骼扭曲，这是因为CCD对连续骨骼进行旋转，旋转轴的一点偏差就能导致旋转的明显不同。

前后向迭代法FABRIK

一种比CCD稍好的算法就是FABRIK算法，全称是前后向迭代法（Forward And Backward Reaching Inverse Kinematics），它找到满意解所需要的循环次数比CCD少。CCD算法通过按关节旋转骨骼让effector和target对齐；而FABRIK则通过移动和缩放骨骼让effector和target对齐，同时该方法还会在前向和后向两个方向去移动骨骼。

接下来看看FABRIK算法的大致思路是什么：

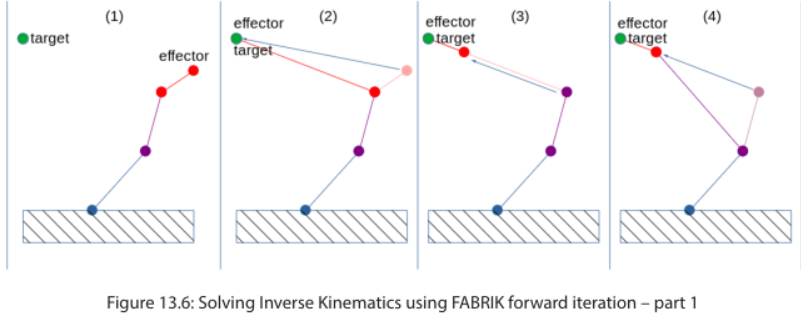
骨骼，Effector和Target的初始状态如下，接下来开始前向遍历求解。
接下来直接将Effector移动到Target上，可以发现和下一个关节的距离远远超出了原骨骼的长度。
为了纠正新骨骼的长度，需要保存移动Effector前骨骼的长度，那么就能将骨骼连带下一个关节缩放至骨骼的原长度。
和第三步相同，需要将红色关节和紫色关节间骨骼的长度缩放至原长。
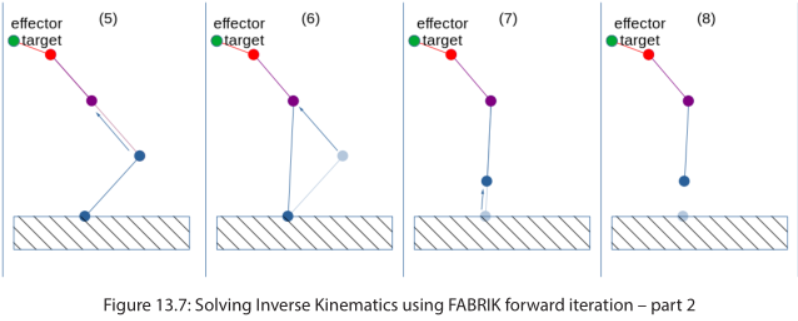
和第三步相同，需要将蓝色关节和紫色关节间骨骼的长度缩放至原长。
按上述步骤处理前向处理完所有节点以后的效果如图8，可以发现根关节脱离了地面，这不是我们想要的。因此接下来要通过 后向遍历处理 来纠正这个结果。
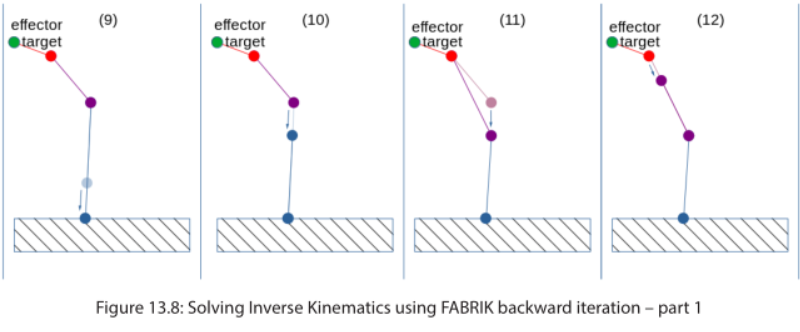
在后向迭代的第一步，需要将根关节恢复至原位置，如图9。
接下来如法炮制，移动后续几个关节，缩放它们骨骼的长度。如图10，11，12.
对于Effector来说也一样，需要缩放它骨骼长度，然后移动它的关节节点，最终结果为图15.

以上就是FABRIK算法一次前向求解和一次后向求解的结果，对比CCD算法的结果来说，该算法的effector离target更近。如果想要提升FABRIK算法的精确度，可以再让它循环求解几次。

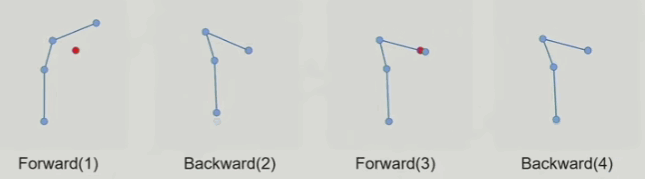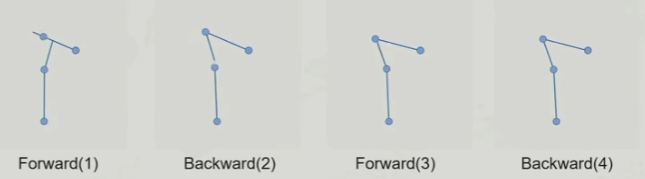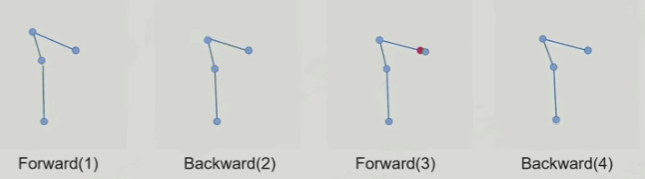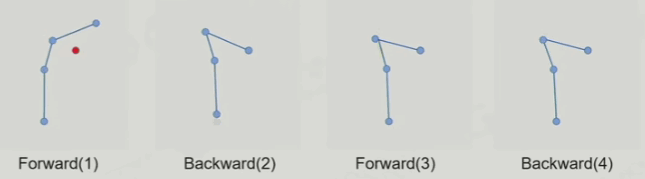
FABRIK算法的动图如下（前向后向各两次遍历）：

接下来尝试实现简易FABRIK算法，代码如下（这段写的不怎么好，有时间优化优化）：

m_isCalcIk = true;

// 准备IK需要的参数
auto boneIDMap = m_currentAnimation->GetBoneIDMap();
// 骨骼原长
std::vector<float> vBoneOriLengths;
vBoneOriLengths.resize(m_ikChainParam.vNodeWorldPosList.size() - 1);
for (int i = 0; i < m_ikChainParam.vNodeWorldPosList.size() - 1; ++i)
{
    glm::vec3 startNodePos = m_ikChainParam.vNodeWorldPosList.at(i);
    glm::vec3 endNodePos = m_ikChainParam.vNodeWorldPosList.at(i + 1);
    vBoneOriLengths.at(i) = glm::length(endNodePos - startNodePos);
}
// 各节点的全局旋转
std::vector<glm::quat> vNodeGlobalRotation;
for (size_t i = 0; i < m_ikChainParam.vpNodeList.size(); ++i)
{
    AssimpNodeData* pCurNode = m_ikChainParam.vpNodeList.at(i);
    Bone* pCurBone = m_currentAnimation->FindBone(pCurNode->name);
    BoneInfo curBoneInfo = boneIDMap[pCurNode->name];

    glm::quat globalRotation = AnimBlendHelper::GetRotationFromMat4(m_finalBoneMatrices[curBoneInfo.id] *
                                                                    curBoneInfo.offset);
    glm::quat localRotation = pCurBone->GetCurOrientation();
    vNodeGlobalRotation.emplace_back(globalRotation);
}
// 各关节的位置(原位置不能被修改)
std::vector<glm::vec3> vNodeCurWorldPos = m_ikChainParam.vNodeWorldPosList;
// 根节点和目标点原来的位置
glm::vec3 targetWorldPos = m_ikChainParam.targetWorldPos;
glm::vec3 rootOriWorldPos = m_ikChainParam.vNodeWorldPosList.back();

// 进行IK
// TODO: 看看能不能封装到一个Solver类里
const float FABRIK_THRESHOLD = 0.00001f;
for (int i = 0; i < m_ikIterationCnt; ++i)
{
    // 符合条件就提前结束
    if (glm::length(targetWorldPos - vNodeCurWorldPos.at(0)) <= FABRIK_THRESHOLD)
    {
        break;
    }

    // 前向求解
    // 1. 将Effector移到Target上
    vNodeCurWorldPos.at(0) = targetWorldPos;
    // 2. 将剩余节点往这里拉
    for (int j = 1; j < vNodeCurWorldPos.size(); ++j)
    {
        glm::vec3 moveDir = glm::normalize(vNodeCurWorldPos.at(j) - vNodeCurWorldPos.at(j - 1));
        glm::vec3 moveOffset = moveDir * vBoneOriLengths.at(j - 1);
        vNodeCurWorldPos.at(j) = vNodeCurWorldPos.at(j - 1) + moveOffset;
    }

    // 后向求解
    // 1. 将根节点移动回原位置
    int rootNodeIdx = vNodeCurWorldPos.size() - 1;
    vNodeCurWorldPos.at(rootNodeIdx) = rootOriWorldPos;
    // 2. 将剩余节点往这里拉
    for (int j = rootNodeIdx - 1; j >= 0; --j)
    {
        glm::vec3 moveDir = glm::normalize(vNodeCurWorldPos.at(j) - vNodeCurWorldPos.at(j + 1));
        glm::vec3 moveOffset = moveDir * vBoneOriLengths.at(j);
        vNodeCurWorldPos.at(j) = vNodeCurWorldPos.at(j + 1) + moveOffset;
    }
}

// 结束IK, 从根节点开始应用骨骼变化
for (int i = vNodeCurWorldPos.size() - 1; i > 0; --i)
{
    AssimpNodeData* pNode = m_ikChainParam.vpNodeList.at(i);
    AssimpNodeData* pChild = m_ikChainParam.vpNodeList.at(i - 1);

    // 获取当前节点的原位置和旋转
    glm::vec3 oriNodeWorldPos = m_ikChainParam.vNodeWorldPosList.at(i);
    glm::quat oriNodeGlobalRotation = vNodeGlobalRotation.at(i);

    // 获取孩子节点的原位置
    glm::vec3 oriChildWorldPos = m_ikChainParam.vNodeWorldPosList.at(i - 1);

    // 计算IK前后node->child的方向
    glm::vec3 toOriChild = glm::normalize(oriChildWorldPos - oriNodeWorldPos);
    glm::vec3 toCurChild = glm::normalize(vNodeCurWorldPos.at(i - 1) - vNodeCurWorldPos.at(i));

    // 获取旋转变化量(World/Global)
    glm::quat oriToCur = glm::normalize(glm::rotation(toOriChild, toCurChild));

    // 获取旋转变化量(Local)
    glm::quat oriToCurLocal = glm::normalize(oriNodeGlobalRotation * oriToCur * glm::conjugate(oriNodeGlobalRotation));

    // 更新当前矩阵
    Bone* pNodeBone = m_currentAnimation->FindBone(pNode->name);
    pNodeBone->SetCurOrientation(glm::normalize(pNodeBone->GetCurOrientation() * oriToCurLocal));
    pNodeBone->SetLocalTransformByCurSRT();

    // 更新矩阵
    glm::mat4 parentTransform = glm::mat4(1.0f);
    AssimpNodeData* pParentNode = pNode->pParentNode;
    if (pParentNode != nullptr)
    {
        BoneInfo rootParentBoneInfo = boneIDMap[pParentNode->name];
        parentTransform = m_finalBoneMatrices[rootParentBoneInfo.id] * glm::inverse(rootParentBoneInfo.offset);
    }

    CalculateBoneTransform(m_currentAnimation, pNode, m_currentTime, parentTransform);

    // 更新世界坐标
    for (int k = i - 1; k >= 0; --k)
    {
        AssimpNodeData* pTmpNode = m_ikChainParam.vpNodeList.at(k);
        BoneInfo tmpBoneInfo = boneIDMap[pTmpNode->name];
        glm::mat4 tmpModelMat = m_ikChainParam.objModelMat *
            m_finalBoneMatrices[tmpBoneInfo.id] * glm::inverse(tmpBoneInfo.offset);
        m_ikChainParam.vNodeWorldPosList.at(k) = tmpModelMat[3];
    }
}

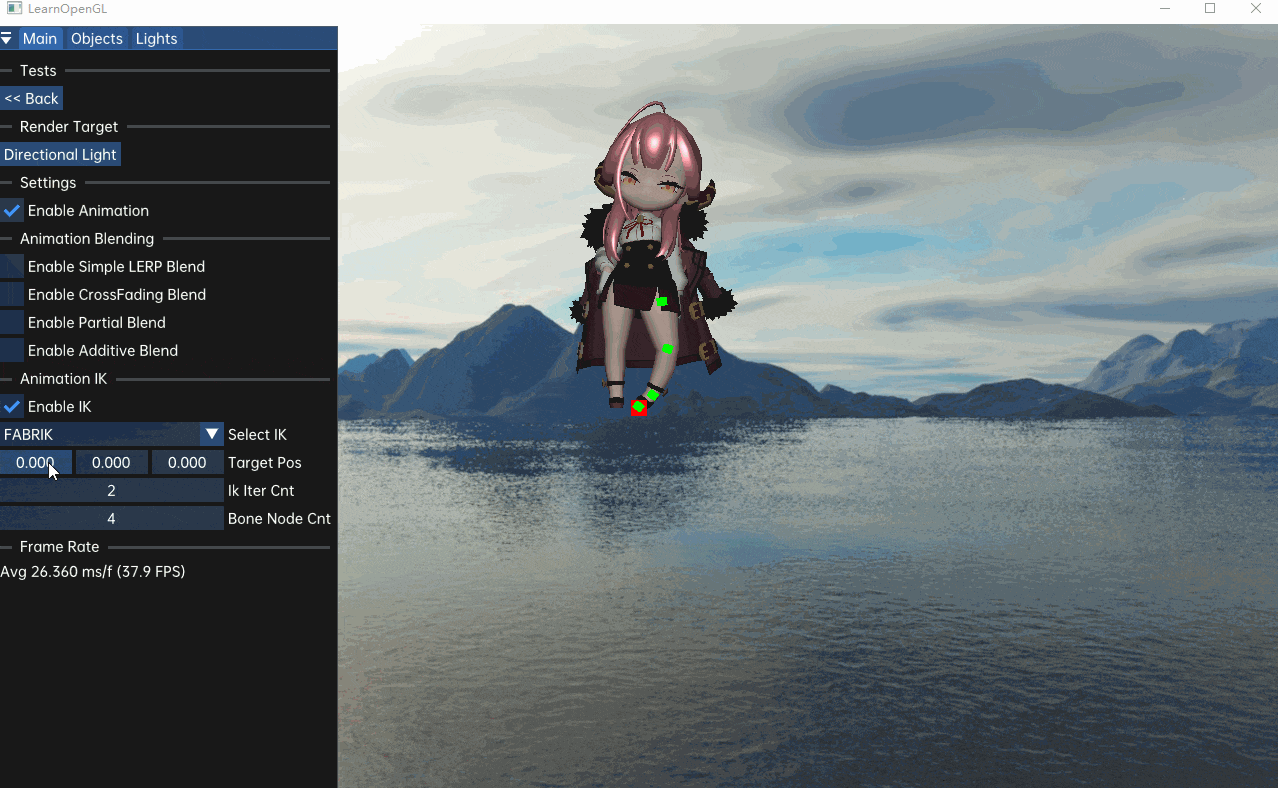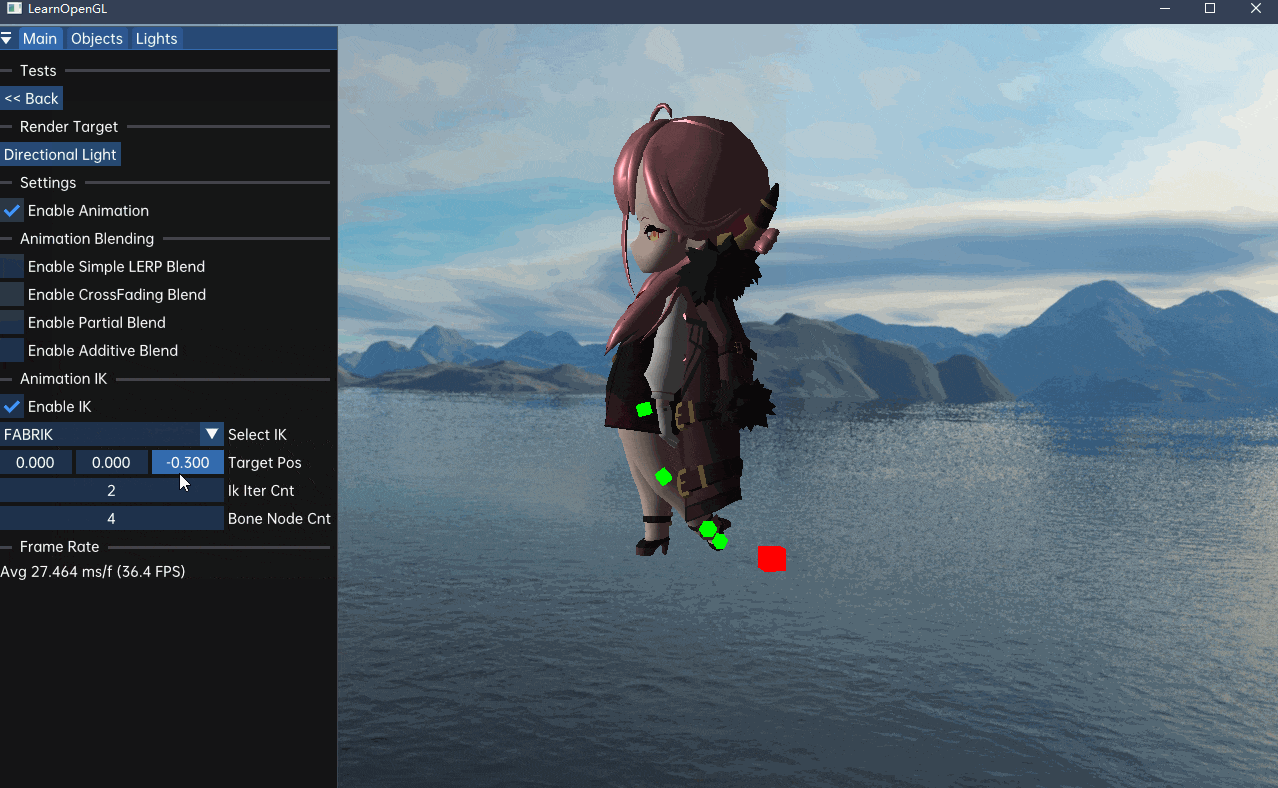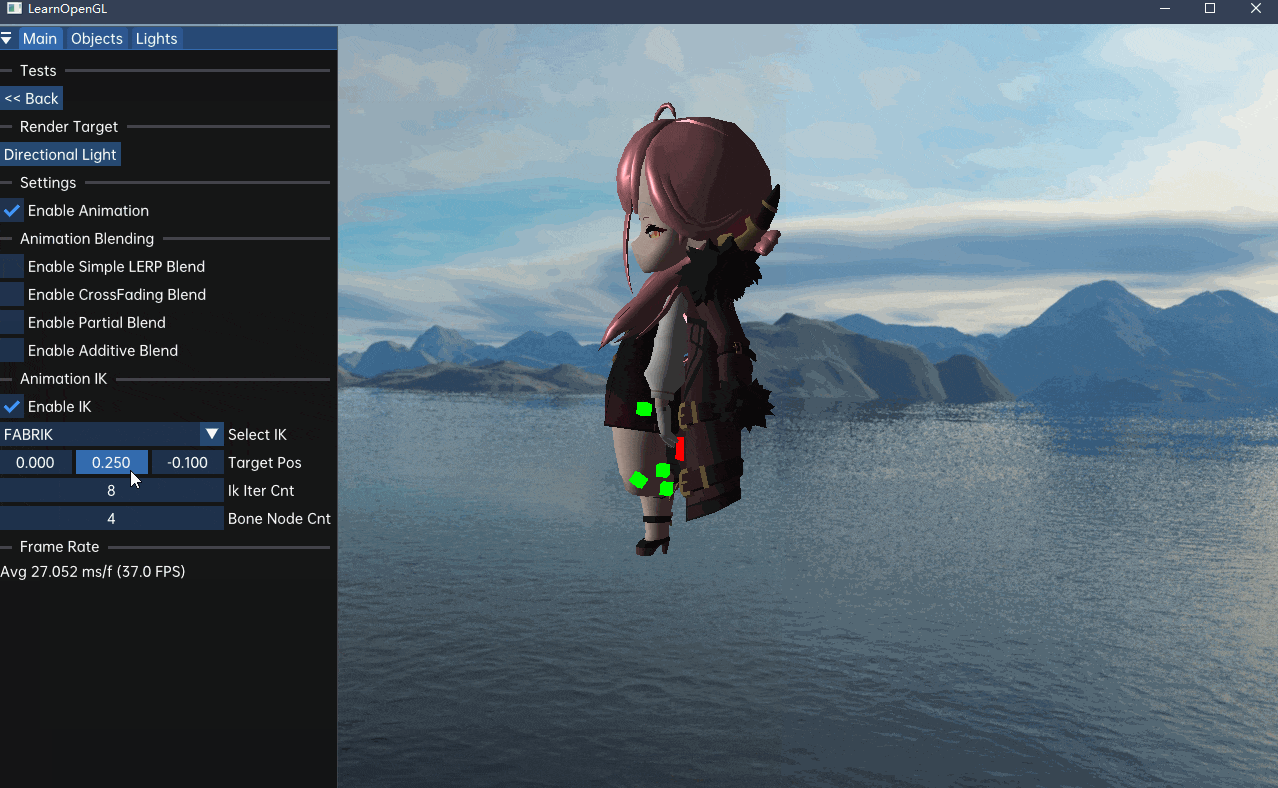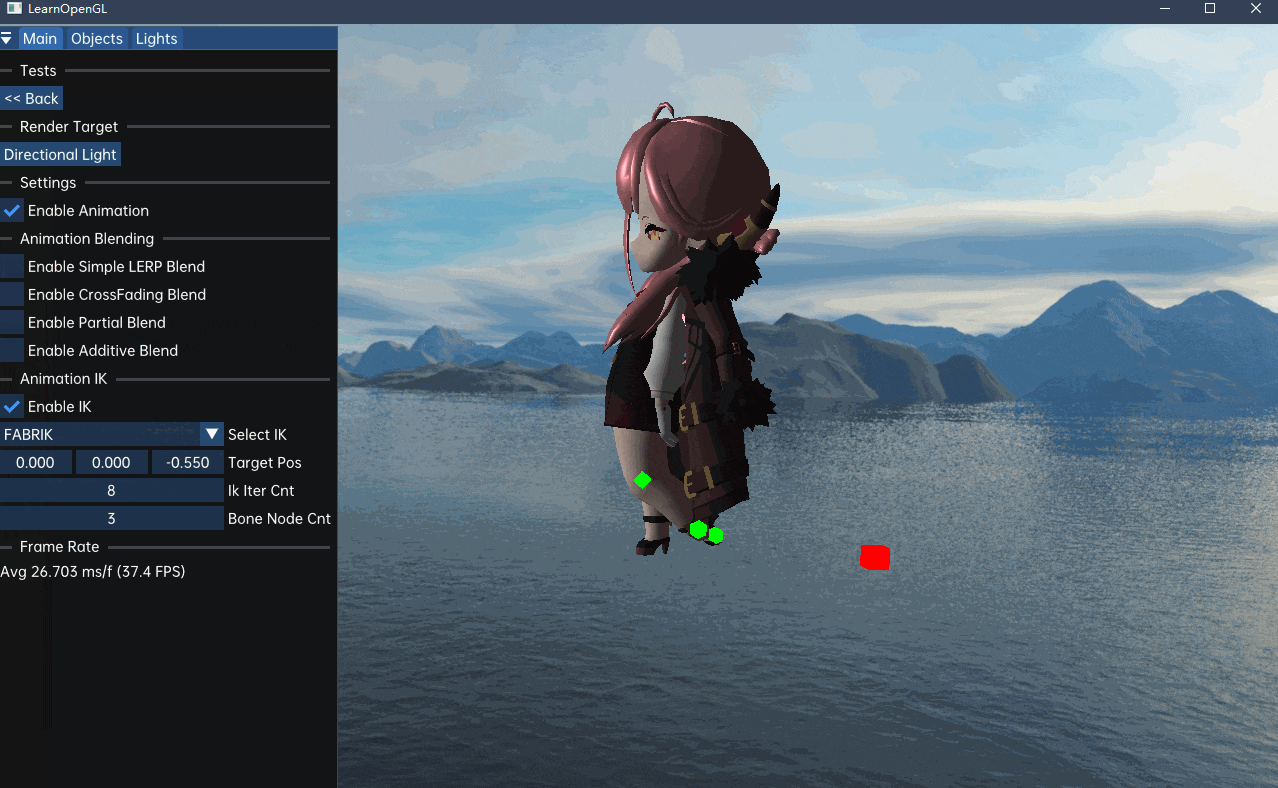
m_isCalcIk = false;

该算法的效果如下：

拓展

可以给IK添加约束，让动画看起来更自然合理。TODO

参考资料

《C++ Game Animation Programming》
Simple Two Joint IK (theorangeduck.com)
常见IK原理 - 知乎 (zhihu.com)