4-法线贴图(Normal mapping)
法线贴图可以让物体看起来更加有凹凸感,增添细节表现。这篇文章将简单展示一下OpenGL中如何实现使用法线贴图。
法线贴图
我们看见的所有物体都由纹理对象(Mesh)组成,每个纹理对象都可能包含了成百上千的三角形面。通过给纹理对象贴上材质,增添了物体的真实感。而法线贴图(Normal/Bump Mapping)可以让物体看起来更加细节,它可以让物体看起来更有凹凸感。
例如砖块,没有法线贴图看起来就是平平的,有法线贴图就有了凹凸感:

虽然我们也可能通过修改高光贴图(Specular map)来想法儿让光线不照亮物体的一部分,从而增添真实感,但效果肯定没法线贴图好,且费时费力。
概念
那什么是法线贴图呢,不着急说,先看看对于光源来说,物体的“表面”是什么:
对于光源来说,他看到的物体“表面”其实就是每个着色点/片段上法向量的综合。因此,改变某点表面法向量,就会让光觉得这个物体“表面”是不平整的:

因此,如果我们可以掌握每个着色点表面的法向量,并将其以RGB的形式存储在一个2D纹理上,这样的纹理/图片就是法线贴图:

由于RGB的范围是[0, 1],我们得先对[-1, 1]的法向量变换到[0,1]上:
vec3 rgb_normal = normal * 0.5 + 0.5; // transforms from [-1,1] to [0,1]通常法线贴图都是蓝色的,因为大多数法向量都指向正z轴(0, 0, 1)。
使用
要想使用法线贴图,仅需在片段着色器中添加如下代码:
uniform sampler2D normalMap;
void main()
{
// 获得[0, 1]的法向量
normal = texture(normalMap, fs_in.TexCoords).rgb;
// [0, 1] -> [-1, 1]
normal = normalize(normal * 2.0 - 1.0);
// 处理光照...
}接下来尝试渲染上面的砖墙例子,结果如下:

漏洞
由于我们使用法线贴图的法线都是指向正Z方向的,如果让砖墙的表面法线指向正Y方向,使用正Z方向的法线贴图就会发生错误:

针对这种漏洞有两种解决方案:
- 为每个表面制作一张单独的法线贴图,如果物体发生变换,也要变换法线贴图上的信息,很是麻烦。
- 在切线空间中进行光照,法线总是指向这个坐标空间的正Z方向;让所有光照向量都相对与这个正Z方向进行变换。这样就能始终使用同样的法线贴图。
切线空间
概念
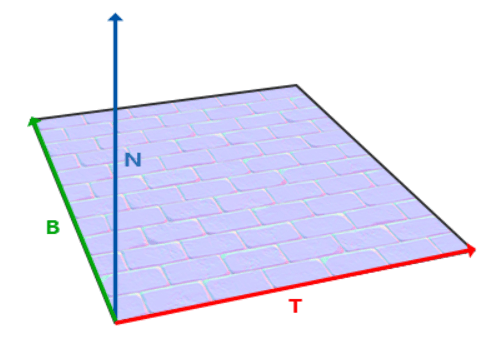
如图,切线空间由三个坐标轴组成,N是表面法线向量,T是切线(Tangent)向量,而B是副切线(Bitangent)向量。
接下来通过数学计算求出T和B:
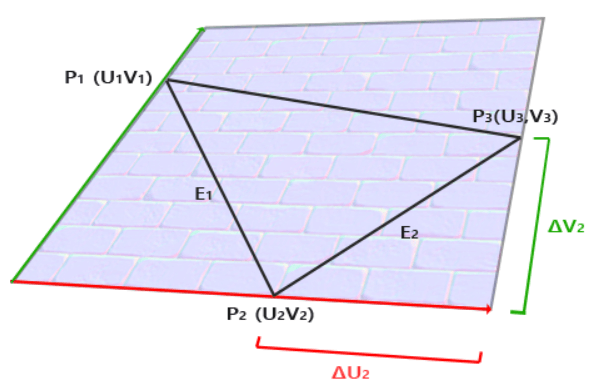
注意到上图中边\(E_2\)和纹理坐标的差\(\mathbf{\Delta U_2,\Delta V_2}\)构成一个三角形。其中\(\mathbf{\Delta U_2}\)的方向和\(\mathbf{T}\)相同,\(\mathbf{\Delta V_2}\)的方向和\(\mathbf{B}\)相同。因此有: \[ \nonumber E_1=\Delta U_1T+\Delta V_1B\\E_2=\Delta U_2T+\Delta V_2B \] 也能写成如下形式: \[ \nonumber (E_{1x},E_{1y},E_{1z})=\Delta U_1(T_x,T_y,T_z)+\Delta V_1(B_x,B_y,B_z)\\(E_{2x},E_{2y},E_{2z})=\Delta U_2(T_x,T_y,T_z)+\Delta V_2(B_x,B_y,B_z) \] 接下来将其改写成矩阵相乘的形式: \[ \nonumber \begin{bmatrix}E_{1x}&E_{1y}&E_{1z}\\E_{2x}&E_{2y}&E_{2z}\end{bmatrix}=\begin{bmatrix}\Delta U_1&\Delta V_1\\\Delta U_2&\Delta V_2\end{bmatrix}\begin{bmatrix}T_x&T_y&T_z\\B_x&B_y&B_z\end{bmatrix} \] 等式两边左乘\(\Delta U,\Delta V\)的逆矩阵,有: \[ \nonumber \begin{bmatrix}\Delta U_1&\Delta V_1\\\Delta U_2&\Delta V_2\end{bmatrix}^{-1}\begin{bmatrix}E_{1x}&E_{1y}&E_{1z}\\E_{2x}&E_{2y}&E_{2z}\end{bmatrix}=\begin{bmatrix}T_x&T_y&T_z\\B_x&B_y&B_z\end{bmatrix} \] 利用\(A^{-1}=\frac1{|A|}A^*\),将逆矩阵消掉有: \[ \nonumber \begin{bmatrix}T_x&T_y&T_z\\B_x&B_y&B_z\end{bmatrix}=\frac{1}{\Delta U_1\Delta V_2-\Delta U_2\Delta V_1}\begin{bmatrix}\Delta V_2&-\Delta V_1\\-\Delta U_2&\Delta U_1\end{bmatrix}\begin{bmatrix}E_{1x}&E_{1y}&E_{1z}\\E_{2x}&E_{2y}&E_{2z}\end{bmatrix} \] 我们便得到\(\mathbf{T,B}\)了。
代码计算
有了公式后,便能计算TBN了。这里手工实现一下如何计算砖墙的TBN,首先需要用到下述向量组成砖墙:
// positions
glm::vec3 pos1(-1.0, 1.0, 0.0); // 1
glm::vec3 pos2(-1.0, -1.0, 0.0); // 2
glm::vec3 pos3(1.0, -1.0, 0.0); // 3
glm::vec3 pos4(1.0, 1.0, 0.0); // 4
// texCoords
glm::vec2 uv1(0.0, 1.0); // 1
glm::vec2 uv2(0.0, 0.0); // 2
glm::vec2 uv3(1.0, 0.0); // 3
glm::vec2 uv4(1.0, 1.0); // 4
// normal
glm::vec3 nm(0.0, 0.0, 1.0);其中,(1,2,3)和(1,3,4)两个三角形组成砖墙。接下来先计算第一个三角形的\(E_1,E_2\)和\(\Delta U,\Delta V\):
glm::vec3 edge1 = pos2 - pos1;
glm::vec3 edge2 = pos3 - pos1;
glm::vec2 deltaUV1 = uv2 - uv1;
glm::vec2 deltaUV2 = uv3 - uv1; 然后就能计算\(T,B\)了:
float f = 1.0f / (deltaUV1.x * deltaUV2.y - deltaUV2.x * deltaUV1.y);
tangent1.x = f * (deltaUV2.y * edge1.x - deltaUV1.y * edge2.x);
tangent1.y = f * (deltaUV2.y * edge1.y - deltaUV1.y * edge2.y);
tangent1.z = f * (deltaUV2.y * edge1.z - deltaUV1.y * edge2.z);
tangent1 = glm::normalize(tangent1);
bitangent1.x = f * (-deltaUV2.x * edge1.x + deltaUV1.x * edge2.x);
bitangent1.y = f * (-deltaUV2.x * edge1.y + deltaUV1.x * edge2.y);
bitangent1.z = f * (-deltaUV2.x * edge1.z + deltaUV1.x * edge2.z);
bitangent1 = glm::normalize(bitangent1);三角形(1, 3, 4)同理。由于点1,3是两个三角形共用的,它们的T和B需要取均值。但这里两个三角形平行,也可以不取均值。
手工计算好的顶点数据如下:
float quadVertices[] = {
// positions // normal // texcoords // tangent // bitangent
pos1.x, pos1.y, pos1.z, nm.x, nm.y, nm.z, uv1.x, uv1.y, tangent1.x, tangent1.y, tangent1.z, bitangent1.x, bitangent1.y, bitangent1.z,
pos2.x, pos2.y, pos2.z, nm.x, nm.y, nm.z, uv2.x, uv2.y, tangent1.x, tangent1.y, tangent1.z, bitangent1.x, bitangent1.y, bitangent1.z,
pos3.x, pos3.y, pos3.z, nm.x, nm.y, nm.z, uv3.x, uv3.y, tangent1.x, tangent1.y, tangent1.z, bitangent1.x, bitangent1.y, bitangent1.z,
pos1.x, pos1.y, pos1.z, nm.x, nm.y, nm.z, uv1.x, uv1.y, tangent2.x, tangent2.y, tangent2.z, bitangent2.x, bitangent2.y, bitangent2.z,
pos3.x, pos3.y, pos3.z, nm.x, nm.y, nm.z, uv3.x, uv3.y, tangent2.x, tangent2.y, tangent2.z, bitangent2.x, bitangent2.y, bitangent2.z,
pos4.x, pos4.y, pos4.z, nm.x, nm.y, nm.z, uv4.x, uv4.y, tangent2.x, tangent2.y, tangent2.z, bitangent2.x, bitangent2.y, bitangent2.z
};写Shader
接下来该利用这些顶点数据了。首先在顶点着色器中获取这些数据:
#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec3 aNormal;
layout (location = 2) in vec2 aTexCoords;
layout (location = 3) in vec3 aTangent;
layout (location = 4) in vec3 aBitangent;然后就能在main()中创建TBN矩阵了:
// 计算TBN
vec3 T = normalize(vec3(model * vec4(aTangent, 0.0)));
vec3 B = normalize(vec3(model * vec4(aBitangent, 0.0)));
vec3 N = normalize(vec3(model * vec4(aNormal, 0.0)));
mat3 TBN = mat3(T, B, N);这里我们先将TBN向量从世界坐标系转换到模型坐标系,然后创建实际的TBN矩阵。如果需要让TBN结果更精准,需要乘法线矩阵,而不是model。此外,B/T求一个就行,另一个可通过cross(N, B/T)求出。
得到TBN矩阵后,就该使用它了,有两种使用它的方式:
- 用TBN矩阵将任何向量从切线空间转换到世界空间,然后丢给片段着色器处理,例如表面法线。处理后的向量和其他光照相关的变量均在世界空间。
- 用TBN矩阵的逆矩阵将任何向量从世界空间转换到切线空间,例如处理光照相关变量。这样处理后的变量就和法线在同一个TBN空间了。
首先看看方式1,利用TBN矩阵将法线转换到世界空间:
// vert
out VS_OUT {
vec3 FragPos;
vec3 Normal;
vec2 TexCoords;
mat3 TBN;
} vs_out;
...
void main()
{
...
vs_out.TBN = mat3(T, B, N);
}然后在片段着色器中使用它:
in VS_OUT {
vec3 FragPos;
vec3 Normal;
vec2 TexCoords;
mat3 TBN;
} fs_in;
...
void main()
{
...
}然后是方式2,利用TBN矩阵的逆矩阵将光照相关变量转换到TBN空间:
out VS_OUT {
vec3 FragPos;
vec3 Normal;
vec2 TexCoords;
// mat3 TBN;
vec3 TangentLightPos;
vec3 TangentViewPos;
vec3 TangentFragPos;
} vs_out;
...
void main()
{
...
// 法2: 用TBN的逆矩阵将光照相关变量转换到TBN空间
mat3 inv_TBN = transpose(mat3(T, B, N));
vs_out.TangentLightPos = inv_TBN * lightPos;
vs_out.TangentViewPos = inv_TBN * viewPos;
vs_out.TangentFragPos = inv_TBN * vec3(model * vec4(aPos, 1.0));
}然后用这些变量在片段着色器中替换一下就行了。结果如下,终于渲染正确了:

复杂物体
对于复杂的物体(如模型),手动计算每个三角形的TBN很麻烦,可以看看Assimp库是怎么做的。
首先,需要在导入的时候添加如下属性:
const aiScene *scene = importer.ReadFile(
path, aiProcess_Triangulate | aiProcess_FlipUVs | aiProcess_CalcTangentSpace
); 这样就能自动计算每个三角形的TBN信息了,然后可以将其存储到对应的顶点信息中:
vector.x = mesh->mTangents[i].x;
vector.y = mesh->mTangents[i].y;
vector.z = mesh->mTangents[i].z;
vertex.Tangent = vector; 为了能在导入时正确计算TBN信息,需要读取模型的法线贴图aiTextureType_NORMAL。对于.obj类型的模型,需要读取aiTextureType_HEIGHT类型的贴图。
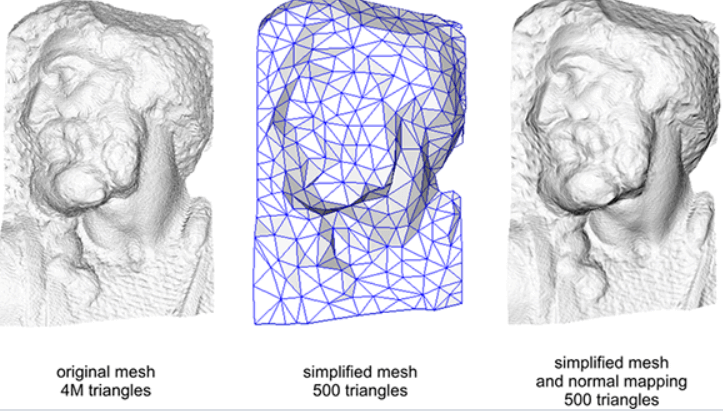
此外,使用法线贴图也能提高场景性能。使用法线贴图可以让我们用更少的三角形表现出差不多丰富的细节:
格拉姆-施密特正交
当在更大的网格计算TBN的时候,由于它们有数量庞大的共享顶点,对TBN进行平均后能获得更平滑的效果。但这样做后TBN可能不是正交的,导致法线贴图出现偏移。可以使用格拉姆-施密特正交,让TBN重新正交化:
// 计算TBN
vec3 T = normalize(vec3(model * vec4(aTangent, 0.0)));
vec3 N = normalize(vec3(model * vec4(aNormal, 0.0)));
// 格拉姆-施密特正交化TN
T = normalize(T - dot(T, N) * N);
// 用正交化后的TN求B
vec3 B = normalize(cross(N, T));参考资料
- LearnOpenGL - Normal Mapping