本文将讨论OpenGL中的几何着色器（Geometry Shader）的用法等。

几何着色器

在顶点和片段着色器之间还有一个可选的几何着色器，它的输入是图元的一组顶点，它可以对这些顶点随意变换，或者生成更多的顶点传递给片段着色器。

基本结构

几何着色器的后缀可以是.geom，一个基本几何着色器的示例如下：

#version 330 core
layout (points) in;
layout (line_strip, max_vertices = 2) out;

void main() {    
    gl_Position = gl_in[0].gl_Position + vec4(-0.1, 0.0, 0.0, 0.0); 
    EmitVertex();

    gl_Position = gl_in[0].gl_Position + vec4( 0.1, 0.0, 0.0, 0.0);
    EmitVertex();

    EndPrimitive();
}

首先，在几何着色器的顶部定义输入和输出类型:

输入类型就是图元，可选的图元如下，其中括号内数字表示该图元至少有几个顶点：

• points：GL_POINTS图元（1）
• lines：GL_LINES或GL_LINE_STRIP（2）
• lines_adjacency：GL_LINES_ADJACENCY或GL_LINE_STRIP_ADJACENCY（4）
• triangles：GL_TRIANGLES、GL_TRIANGLE_STRIP或GL_TRIANGLE_FAN（3）
• triangles_adjacency：GL_TRIANGLES_ADJACENCY或GL_TRIANGLE_STRIP_ADJACENCY（6）

输出类型是图元+最大顶点数，OpenGL不会绘制多出的顶点，可选的图元如下：

• points
• line_strip
• triangle_strip

line_strip就是每增加一个点，该点会与上一个点之间进行连线。这里最大顶点为2，只能生成一个线段。

triangle_strip同理，就是绘制完第一个三角形后，每个后续顶点都会以上一个三角形一边为基础生成一个新的三角形。

然后就是对顶点的处理了。其中，注意到一个内建变量gl_in[]，它包含了我们需要的一组顶点信息，在内部可能是这样的：

in gl_Vertex
{
    vec4  gl_Position;
    float gl_PointSize;
    float gl_ClipDistance[];
} gl_in[];

还有两个内建函数EmitVertex()和EndPrimitive()，前者会将新增的顶点信息添加到图元（本例以输入顶点为中心，添加了两个新顶点（往前和往后平移的）），后者会将新增的顶点合成为指定的输出图元（本例是一个线段）。

它的效果如下：

使用

画一个2D房子。我们需要以points为输入图元，triangle_strip为输出图元，这需要以正确的顺序去绘画三角形。

房子的原理图如下：

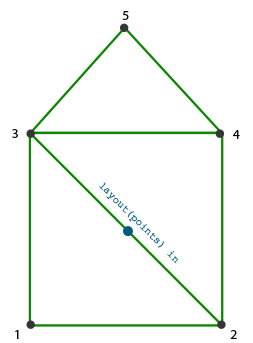
几何着色器代码如下：

#version 330 core
layout (points) in;
layout (triangle_strip, max_vertices = 5) out;

void build_house(vec4 position)
{    
    gl_Position = position + vec4(-0.2, -0.2, 0.0, 0.0);    // 1:左下
    EmitVertex();   
    gl_Position = position + vec4( 0.2, -0.2, 0.0, 0.0);    // 2:右下
    EmitVertex();
    gl_Position = position + vec4(-0.2,  0.2, 0.0, 0.0);    // 3:左上
    EmitVertex();
    gl_Position = position + vec4( 0.2,  0.2, 0.0, 0.0);    // 4:右上
    EmitVertex();
    gl_Position = position + vec4( 0.0,  0.4, 0.0, 0.0);    // 5:顶部
    EmitVertex();
    EndPrimitive();
}

void main() {    
    build_house(gl_in[0].gl_Position);
}

最终效果如图：

有了几何着色器，可以将一个简单的点图元变成房子。因为这些形状是在GPU的超快硬件中动态生成的，这会比在顶点缓冲中手动定义图形要高效很多。因此，几何缓冲对简单而且经常重复的形状来说是一个很好的优化工具，比如体素(Voxel)世界中的方块和室外草地的每一根草。

实践：3D物体的爆破效果

实现3D物体的爆破效果很简单，只需把每个图元往它法线方向移动即可。

在几何着色器中，可以通过计算平行于三角形平面两个向量的叉乘来得到对应的法向量：

vec3 getNormal()
{
    vec3 a = vec3(gl_in[0].gl_Position) - vec3(gl_in[1].gl_Position);
    vec3 b = vec3(gl_in[2].gl_Position) - vec3(gl_in[1].gl_Position);
    return normalize(cross(a, b));
}

然后就能将图元沿着法线位移了，这里引入一个时间uniform变量，让每个图元能够按规律运动：

vec4 explode(vec4 position, vec3 normal)
{
    float magnitude = 2.0;
    vec3 dir = normal * ((sin(time) + 1.0) / 2.0) * magnitude;
    return position + vec4(dir, 0.0);
}

main()函数如下：

void main()
{    
    vec3 normal = getNormal();

    // 三角形有3个顶点
    gl_Position = explode(gl_in[0].gl_Position, normal);
    TexCoords = gs_in[0].texCoords;
    EmitVertex();
    gl_Position = explode(gl_in[1].gl_Position, normal);
    TexCoords = gs_in[1].texCoords;
    EmitVertex();
    gl_Position = explode(gl_in[2].gl_Position, normal);
    TexCoords = gs_in[2].texCoords;
    EmitVertex();

    EndPrimitive();
}

实践：图元法向量可视化

接下来要可视化模型三角形表面的法向量，可以先把普通模型渲染一遍，然后再用几何着色器将表面的三根法向量渲染出来。

// vert
#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec3 aNormal;

out VS_OUT {
    vec3 normal;
} vs_out;

uniform mat4 view;
uniform mat4 model;

void main()
{
    gl_Position = view * model * vec4(aPos, 1.0); 
    mat3 normalMatrix = mat3(transpose(inverse(view * model)));
    vs_out.normal = normalize(vec3(vec4(normalMatrix * aNormal, 0.0)));
}

// geom
#version 330 core
layout (triangles) in;
layout (line_strip, max_vertices = 6) out;

in VS_OUT {
    vec3 normal;
} gs_in[];

const float MAGNITUDE = 0.2;

uniform mat4 projection;

void GenerateLine(int index)
{
    gl_Position = projection * gl_in[index].gl_Position;
    EmitVertex();
    gl_Position = projection * (gl_in[index].gl_Position + 
                                vec4(gs_in[index].normal, 0.0) * MAGNITUDE);
    EmitVertex();
    EndPrimitive();
}

void main()
{
    GenerateLine(0); // 第一个顶点法线
    GenerateLine(1); // 第二个顶点法线
    GenerateLine(2); // 第三个顶点法线
}

// frag
#version 330 core
out vec4 FragColor;

void main()
{
    FragColor = vec4(1.0, 1.0, 0.0, 1.0);
}

注意，在顶点着色器中先不进行投影变换，因为我们画的应该是法线而不是模型本身，因此得在几何着色器中进行投影变换。

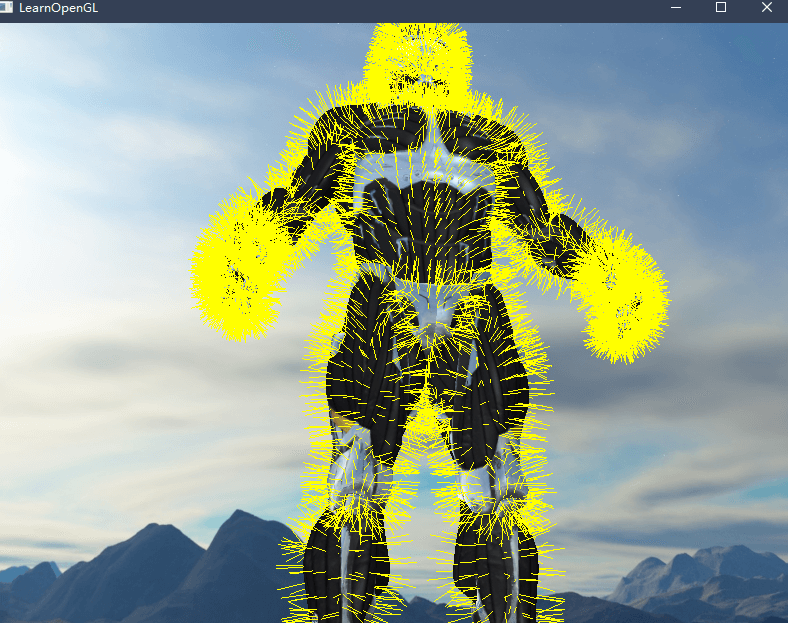
参考资料

• 几何着色器 - LearnOpenGL CN (learnopengl-cn.github.io)