3 - 混合
OpenGL中,混合(Blending)通常是实现物体透明度的一种技术。例如透过玻璃去看物体:

Alpha值
介绍
一个物体的透明度由它颜色的Alpha值(即RGBA中的A)决定,范围是0~1,0是完全透明,1是不透明。
例如下图窗户纹理,它玻璃部分的透明度就是0.25:

利用alpha值丢弃片段
接下来,我们尝试在OpenGL中显示这个草,只需将其贴在一个2D四边形平面上就好。

先给草写一个片段着色器,注意这里使用了纹理的RGBA分量:
#version 330 core
out vec4 FragColor;
in vec2 TexCoords;
uniform sampler2D grassTexture;
void main()
{
FragColor = texture(grassTexture, TexCoords).rgba;
}效果如下:

可以发现,还有讨厌的白色部分存在,我们可以利用GLSL中的discard命令来把这些白色片段给丢弃了:
vec4 texColor = texture(grassTexture, TexCoords).rgba;
if (texColor.a < 0.1)
discard;如果纹理的alpha值低于0.1,就丢弃这个片段。效果如下:

混合
直接丢弃片段的缺点就是 不能渲染半透明图像,如果想渲染半透明图像,得启用混合:
glEnable(GL_BLEND);OpenGL的混合原理
OpenGL通过下面的方程实现混合: \[ \nonumber \mathbf{C_{result}=C_{source}\times F_{source} + C_{destination}\times F_{destination}} \] 各项的含义如下:
- \(C_{source}\):源自纹理的颜色向量
- \(C_{destination}\):目标颜色向量,即当前存储在颜色缓冲中的向量
- \(F_{source}\):指定alpha值对源颜色的影响
- \(F_{destination}\):指定alpha值对目标颜色的影响
例如将下图中的红色方形与绿色方形混合,且绿色方形覆盖在红色方形之上,那么红色方形就是目标颜色:
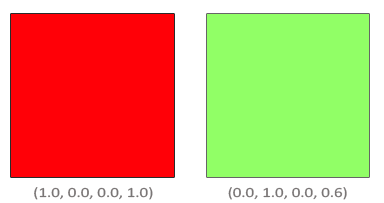
OpenGL会这样计算结果: \[ \nonumber \mathbf{C_{result}}= \begin{pmatrix} 0\\ 1\\ 0\\ 0.6 \end{pmatrix} \times0.6+ \begin{pmatrix} 1\\ 0\\ 0\\ 1 \end{pmatrix} \times (1-0.6) \] 其中,绿色方形对最终颜色贡献了60%,红色的是40%。最后得到的结果如下:
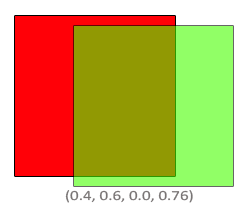
混合的实现
glBlendFunc()
OpenGL中有个叫做glBlendFunc()的函数,它接收两个参数用来设置\(F_{src}\)和\(F_{dest}\)。常见的参数列表如下:
| 选项 | 值释义 |
|---|---|
GL_ZERO | 因子等于0 |
GL_ONE | 因子等于1 |
GL_SRC_COLOR | 因子等于源颜色向量\(C_{source}\) |
GL_ONE_MINUS_SRC_COLOR | 因子等于1−\(C_{source}\) |
GL_DST_COLOR | 因子等于目标颜色向量\(C_{destination}\) |
GL_ONE_MINUS_DST_COLOR | 因子等于1−\(C_{destination}\) |
GL_SRC_ALPHA | 因子等于\(C_{source}\)的alpha分量 |
GL_ONE_MINUS_SRC_ALPHA | 因子等于1− \(C_{source}\)的alpha分量 |
GL_DST_ALPHA | 因子等于\(C_{destination}\)的alpha分量 |
GL_ONE_MINUS_DST_ALPHA | 因子等于1− \(C_{destination}\)的alpha分量 |
GL_CONSTANT_COLOR | 因子等于常数颜色向量\(C_{constant}\) |
GL_ONE_MINUS_CONSTANT_COLOR | 因子等于1−\(C_{constant}\) |
GL_CONSTANT_ALPHA | 因子等于\(C_{constant}\)的alpha分量 |
GL_ONE_MINUS_CONSTANT_ALPHA | 因子等于1− \(C_{constant}\)的alpha分量 |
其中,可以通过glBlendColor()来设置\(C_{constant}\)。
对于上边的两个方形例子,它对应的glBlendFunc()代码如下:
// 让源alpha作为Fsrc,让(1 - 源alpha)作为Fdest
glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA)glBlendFuncSeparate()
如果要更细致地分别设置RGB和Alpha通道的相关值,可以使用此函数:
glBlendFuncSeparate(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA, GL_ONE, GL_ZERO);glBlendEquation()
该函数可以修改混合方程的算术运算符:
- GL_FUNC_ADD:默认选项,将两个分量相加:Res = Src + Dst
- GL_FUNC_SUBTRACT:将两个分量相减:Res = Src - Dst
- GL_FUNC_REVERSE_SUBTRACT:将两个分量相减,但顺序相反:Res = Dst - Src
不过大部分情况下不会用到这个函数。
实践:实现半透明玻璃效果
接下来开始利用混合技术实现上边提到的半透明玻璃效果。
初步实现
只需启用混合,并设定混合函数即可:
glEnable(GL_BLEND);
glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);记得把片段着色器还原(去掉discard部分)。结果如下图:
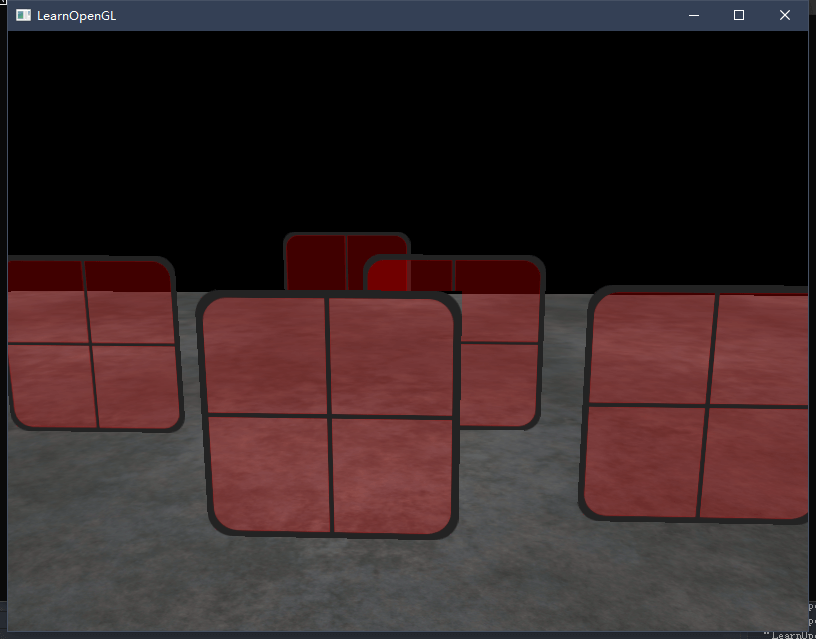
可以发现半透明效果是实现了,但深度测试又出了问题,有的玻璃从前面看不见后面的玻璃,而有的玻璃却可以。
原因就是当写入深度缓冲时,深度缓冲不会检查片段是否是透明的,导致整个窗户(包括玻璃部分)都要进行深度测试。要想保证所有窗户都能显示它们背后的窗户,只能从远往近按顺序渲染窗户了。
按顺序渲染
当场景中有透明和不透明的物体时,绘制它们的步骤如下:
- 绘制所有不透明的物体
- 对所有透明的物体排序
- 按顺序绘制所有透明的物体
可以从观察者视角获取到它离物体的距离,然后对透明物体进行排序。
// 对透明物体排序
std::map<float, glm::vec3> sorted;
for (unsigned int i = 0; i < vegetation.size(); i++)
{
float dist = glm::length(camera.Position - vegetation[i]);
sorted[dist] = vegetation[i];
}
for (auto it = sorted.rbegin(); it != sorted.rend(); ++it)
{
// ...
}结果正确了:
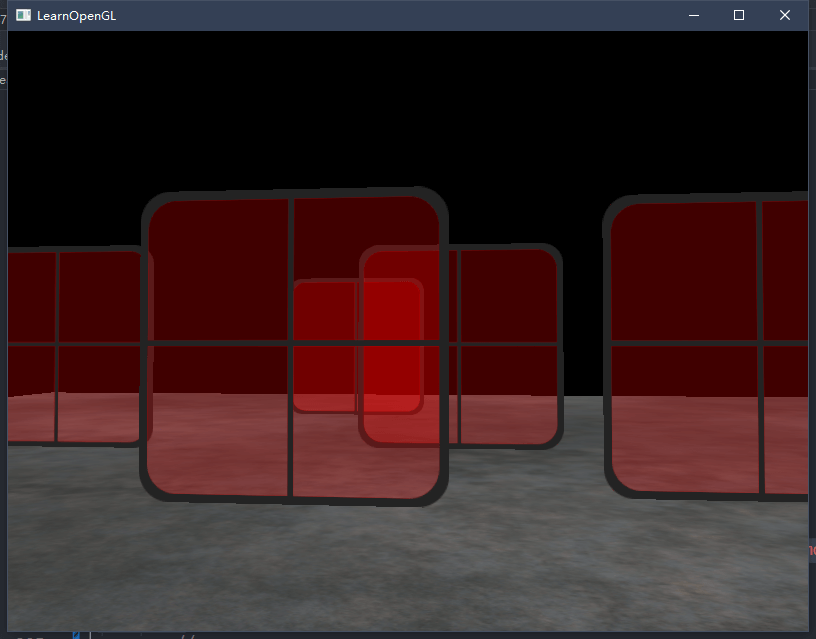
在本次实践中,这样处理就可以了。但实际上,它并没有考虑旋转、缩放或者其它的变换,奇怪形状的物体需要一个不同的计量,而不是仅仅一个位置向量。
完整渲染一个包含不透明和透明物体的场景并不是那么容易。更高级的技术还有次序无关透明度(Order Independent Transparency, OIT)等。
参考资料
- 混合 - LearnOpenGL CN (learnopengl-cn.github.io)