本文将会对各种各样的光源进行一个讨论，例如 定向光(Directional Light)，点光源(Point Light)和聚光(SpotLight)。

平行光/定向光

当我们使用一个离模型 无限远 的光源时，打到物体上的每条光线近似于互相平行，这就是 定向/平行光源。比如太阳。

可以定义一个光线方向向量而不是用位置向量来模拟一个定向光：

struct DriectionalLight
{
    // 方向：光源 -> 着色点
    vec3 direction;

    vec3 ambient;
    vec3 diffuse;
    vec3 specular;
};
    
void main()
{
    // ...
    vec3 lightDir = normalize(-light.direction); // 方向：着色点 -> 光源
}

接下来再绘制十个位于不同位置的箱子，康康平行光对它们的影响（由于这些箱子共用一个Shader实例，导致箱子发光面没有符合常识）：

点光源

除了平行光之外，构成全局光源的存在还有点光源（Point Light）。点光源是出于世界中某一个位置的光源，它会朝着所有方向发光，但光线会随着距离衰减强度。比如火把。

光线的衰减

在之前实现的Blinn-Phong光照模型中就是用的点光源，距离衰减函数被定义为\(I/r^2\)，这个函数是线性的，效果不大好且不现实。这时需要用这个公式来计算光的衰减值： \[ \nonumber F_{att}=\frac{1.0}{K_c+K_ld+K_qd^2} \] 公式的含义如下：

• d代表着色点距离光源的距离；
• 常数项Kc通常为1.0，主要作用是保证分母永远不会比1小；
• 一次项Kl会以距离值相乘，以线性的方式减少强度；
• 二次项kq会与距离的平方相乘，以二次递减的方式减少强度。

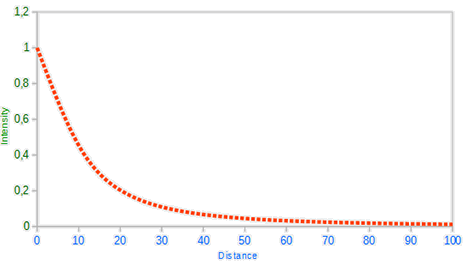
利用该公式计算出来的衰减值去算100距离内的光强结果如图，可以发现光强首先巨幅衰减，然后缓慢衰减，符合常识。

对于这些项该取那些值，这里有相关资料，下图显示模拟一个大概真实、覆盖特定半径/距离的光源时，这三个项取的值：

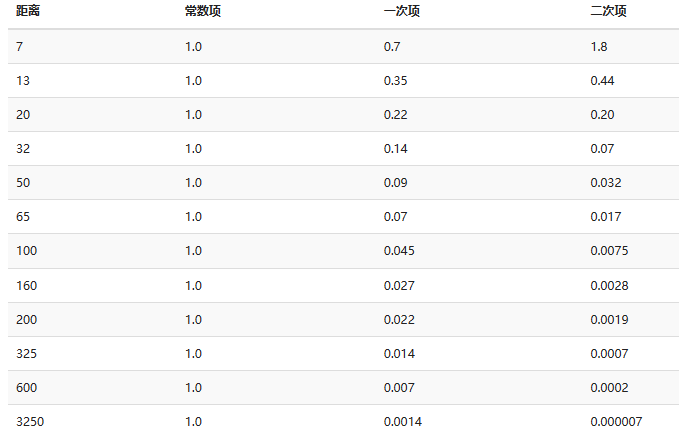
实现点光源

接下来在OpenGL中实现点光源，首先先修改物体的片段着色器，让其拥有点光源的相关参数：

struct PointLight
{
    vec3 position;

    vec3 ambient;
    vec3 diffuse;
    vec3 specular;

    float constant;
    float linear;
    float quadratic;
};

然后设置相关值，这里让光源覆盖50的距离：

cubeShader.setFloat("light.constant", 1.0f);
cubeShader.setFloat("light.linear", 0.09f);
cubeShader.setFloat("light.quadratic", 0.032f);

最后在着色器中计算衰减值：

float d = length(light.position - FragPos);
float attenuation = 1.0 / (light.constant + light.linear * d + light.quadratic * (d * d));

vec3 result = (ambient + diffuse + specular) * attenuation + emission;

可以看到，光线确实是衰减的：

点光源就是一个能够配置位置和衰减的光源。它是我们光照工具箱中的又一个光照类型。

聚光(SpotLight)

聚光是位于环境中某个位置的光源，只朝一个特定方向而不是所有方向照射光线。这样做的结果就是只有在聚光方向的特定半径内物体才会被照亮。例如手电筒、路灯。

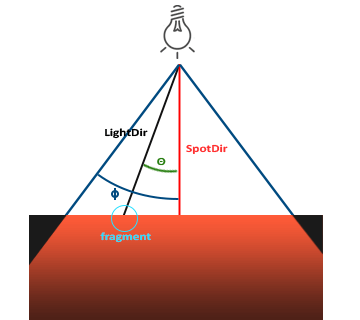
如图，聚光可用 一个世界空间位置，一个方向和一个切光角（Cut-off Angle）来表示，将一些量拆开后，变成如下几个量：

• LightDir：从着色点/片段指向光源的向量
• SpotDir：聚光指向的方向
• Phi\(\Phi\)：指定了聚光半径（圆锥的半径）的切光角，该角度外的物体不会被聚光照亮。
• Theta\(\Theta\)：LightDir和SpotDir的夹角，在聚光内部的话应有\(\Theta \leq \Phi\)。

为了方便计算，之后都将角度值转换为余弦值进行计算。

实现手电筒

接下来尝试实现一个手电筒，手电筒是普通的聚光，他的位置和方向就是摄像机的位置和面前朝向。

首先在片段着色器中更新聚光的结构体：

struct SpotLight
{
    vec3 position;
    vec3 direction;
    float cutOff;

    vec3 ambient;
    vec3 diffuse;
    vec3 specular;
};

然后将合适的值传入着色器中：

cubeShader.setVec3("light.position", camera.Position);
cubeShader.setVec3("light.direction", camera.Front);
cubeShader.setFloat("light.cutOff", glm::cos(glm::radians(12.5f)));

最后修改片段着色器，如果片段在聚光内部就给他所有光，否则只有环境光和自发光：

// 聚光相关计算
float theta = dot(lightDir, normalize(-light.direction));
vec3 result = ambient + emission;
if (theta > light.cutOff)
{
    // ...
    result += diffuse + specular;
}

FragColor = vec4(result, 1.0);

最终效果如下，但还是有点不真实，因为聚光的边缘没有平滑的过渡：

实现平滑过渡

接下来尝试实现平滑过渡的聚光。让聚光拥有一个内圆锥和一个外圆锥，内圆锥就是上边的手电筒效果，然后再加一个外圆锥，让光从内圆锥边界逐渐变暗至外圆锥的边界。

创建一个外圆锥，用余弦值\(\gamma\)来代表聚光方向向量和外圆锥边界向量的夹角（即外圆锥的切光角）。如果一个片段位于内外圆锥间，将会给它计算出一个\((0.0,1.0)\)的强度值，在内圆锥内就是1.0，在外圆锥外就是0.0。

可以用下边这个公式来计算强度值： \[ \nonumber I=\frac{\theta-\gamma}{\epsilon} \] 其中，\(\epsilon\)是内圆锥切光角\(\phi\)余弦值与外圆锥切光角\(\gamma\)余弦值之差。该公式就是根据着色点与聚光方向的夹角\(\theta\)来插值。

修改片段着色器：

// 聚光相关计算
float theta = dot(lightDir, normalize(-light.direction));
float epsilon = light.cutOff - light.outerCutOff;
float intensity = clamp((theta - light.outerCutOff) / epsilon, 0.0, 1.0);

// 距离衰减
float dist = length(light.position - FragPos);
float attenuation = 1.0 / (1.0 + light.linear * dist + light.quadratic * (dist * dist));

return (ambient + diffuse + specular) * intensity * attenuation;

内圆锥切光角12.5°，外圆锥切光角17.5°，如图，有恐怖游戏那味了：

参考资料

• 俺仿写的代码。
• 投光物 - LearnOpenGL CN (learnopengl-cn.github.io)