本文将简要介绍RTRT在空间上的降噪/复用技术——滤波（双边、联合双边），以及如何实现较大的滤波器，和Outlier Removal这一思想。

滤波

滤波的实现

假设要实现一个低通滤波，它保留图片的低频信息，并去掉高频噪声。

输入：有噪声的图，一个滤波核

输出：降噪后的图

以高斯滤波核为例（也有指数、余弦等核），任何在像素i周围的像素j都有可能对i有贡献，这取决与它俩间的距离。

伪代码如下：

sum_of_weights = sum_of_weighted_values = 0.0
For each pixel j around i
		Calculate the weight w_ij = G(|i - j|, sigma)
	sum_of_weighted_values += w_ij * C^{input}[j]
	sum_of_weights += w_ij
C^{output}[I] = sum_of_weighted_values / sum_of_weights

Ps：

• 存储sum_of_weights是为了最后的“归一化(Normalization)”操作。
• 最终结果不可能为0，因为像素i本身也有贡献。但使用其他的滤波核降噪结果可能为0，因此使用其他滤波核时要进行零值检查。
• 要过滤的值可以是RGB多通道的。

高斯滤波处理后的图片会变模糊。

双边滤波

高斯滤波处理后的图片会变模糊，如果我们仍想保留图片“边界(Boundary)”的高频信息，就要使用 双边滤波(Bilateral Filtering)。

双边滤波认为“边界”就是图像中颜色变化剧烈的地方。为了保留边界，需要让像素j和要滤波的像素i比较颜色差异：

• 差异很大，减少像素j对像素i的贡献
• 差异不大，按正常高斯滤波操作

因此有 其中exp()第一项是高斯滤波核，第二项是差异，I(x,y)是点(x,y)的像素值。

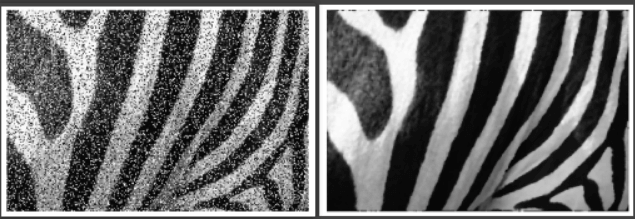
可见效果还不错，为大量有边界的色块。但仍有部分噪点未被消除，因为双边滤波认为部分噪声也是边界。

联合双边滤波

高斯滤波根据像素i和j的“距离”判断贡献，双边滤波根据像素i和j的“位置距离”和“颜色距离”判断贡献。因此可以 考虑用更多的条件约束贡献，这种思想就是Cross/Joint。

联合双边滤波（Joint Bilateral filtering）特别适合对路径追踪的结果进行降噪。可以用G-Buffer中 无噪声 的信息作为条件约束贡献。

以这张图为例，看看如何做联合双边滤波：

对于A，B这种深度差异大的情况，可以用深度信息作为约束判断贡献；对于B，C这种法线差异大的情况，可以用法线信息作为约束判断贡献；对于D，E这种颜色差异大的情况，可以用颜色信息作为约束判断贡献。

实现大的滤波器

直接遍历

对于比较小的滤波器（如7x7），可以在遍历噪声图每个像素的同时遍历它周围7x7个邻居。而对于大的滤波器（64x64）时间消耗很大，因此要找到其他解决方法。

拆分滤波核

一种方法是拆分滤波器，进行分批滤波。例如一个2D的高斯滤波核（NxN），可以先做水平的1xN滤波，然后再做竖直的Nx1滤波。复杂度由降低至。

这是因为2D的高斯滤波核本身是可拆分的（由滤波和卷积关系推出）：

理论上，(联合)双边滤波核是不可拆分的，但对小于32x32的滤波核进行拆分影响也不大。

逐步增长滤波核

也可以使用逐步增大的滤波核进行多次滤波操作，例如A-trous wavelet变换：

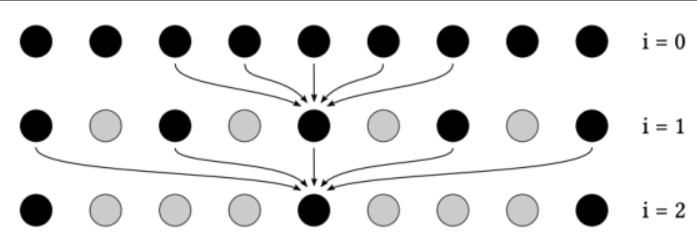
每次进行5x5的滤波，并且点的间隔为。以做64x64滤波为例，原本复杂度为，现在仅需（做5层5x5）的滤波。

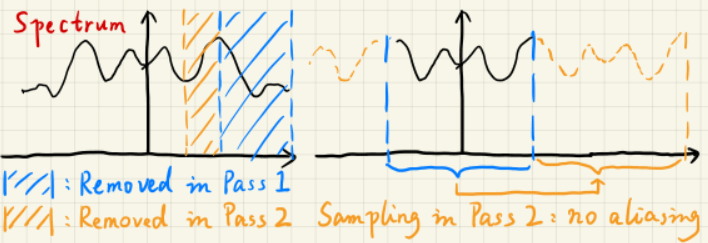
逐渐增大滤波核，图像会失去越低的频率；由于采样相当于重复频谱图，所以可以间隔点采样。通过上一趟采样，把上一趟能表示的频率范围限制起来，下一趟采样时对频谱图“重复采样”不会出现走样现象。

这个方法最后可能仍保留部分高频信息，导致出现格状瑕疵。仅需用小滤波核再滤波一次即可。

Outlier Removal

对于未降噪的当前帧画面，结果可能有不在0~255范围内的噪点，如果进行简单降噪，这个噪点会影响其他区域，让结果更糟。这些超出范围的噪点被称为Outlier。

因此，我们需要在滤波操作前处理掉Outlier，这个操作就是Outlier Removal。它的做法是：

1. 找到Outlier：对于每个像素，取它周围的7x7，记录颜色的均值和方差。认为像素值不在内的就是Outlier。

2. 处理Outlier：对Outlier使用clamp()操作即可，范围就是上边的。

   Ps：工业界对于clamp()的范围有更细致的讨论。

参考资料

• GAMES202: 高质量实时渲染 (ucsb.edu)