早期为了优化PCSS的性能问题，人们想出了使用VSSM(Variance Soft Shadow Mappnig)，本文将简要介绍一下它的思路。另外文末将简要介绍一下VSSM的优化——MSM(Moment Shadow Mapping)。

VSSM

引入

PCSS的第一步（块查询）和第三步（PCF）太慢了，得想法子优化：

• 对于第一步，就是要想出一个更快的块查询算法；

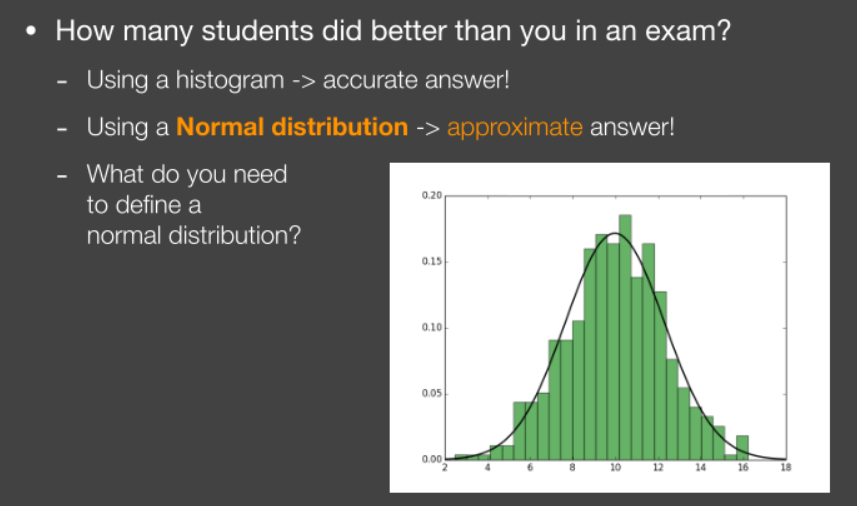
• 对于第三步该怎么进行优化呢，先想一个问题：考试后知道自己的成绩，求自己排名？有两种解法：

  精确解法：问每个人成绩，得到成绩分布直方图，从而得到具体排名。

  近似解法：使用正态分布，根据自己成绩可得出近似排名。

而这个近似解法正是VSSM所采用的思想，会用到一个不具体的分布，然后得出有多少纹素的深度值比自己低。

思路

VSSM的核心思路就是 快速计算某区域内深度的均值(Mean/Avg)与方差(Variance)。

求均值

可以使用Mipmap（不怎么准，只能求方形纹理）；也可以使用 Summed Area Tables（SAT）。SAT的具体内容将在下文中考虑。

求方差

需要用到如下公式： 根据公式，我们需要得到深度值和它的平方，因此需要两个SM。为了节省空间，可将两个SM分两个通道存储在一个纹理中。

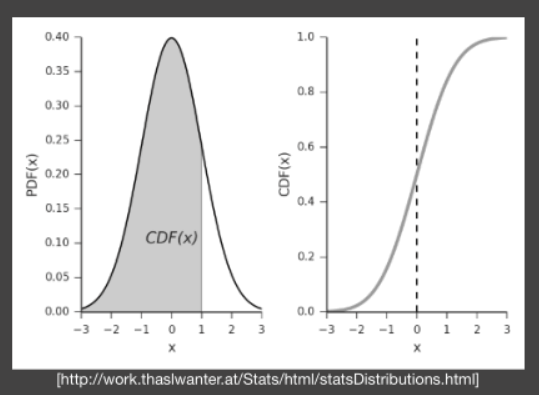
求解CDF(depth)

CDF(depth) 就是在某分布PDF(depth) 中，depth所占的比例。

一种简单暴力的解法就是用C++的exf()函数打表求出CDF(depth)的数值解，然后查表，比较复杂。

但在RTR领域中，我们没必要去消耗大量算力求精确解，只需求近似解即可。为了求CDF(depth)的近似解，需要用到 切比雪夫不等式(Chebychev’s inquality)：

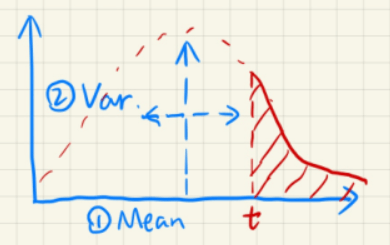
使用该不等式，就 不需要了解具体分布，在知道均值和方差后，可以得出随机变量的大概概率。

那么，该不等式的使用前提是：要求的depth应大于均值，否则结果不准确。

性能分析

1. 生成SM：用双通道存储纹素的深度值和深度值的平方；用SAT求均值/用Mipmap求均值……
2. 运行时：范围内深度值均值、均值的平方可由求出，那么根据与切比雪夫不等式，CDF(depth)也可由求出。
3. 获得结果：用CDF(depth)可求出每个点的可见性。

用SAT求均值

思路

将区域内的深度值均值分为两种：

• 遮挡物(z < depth)的深度值均值，这是我们要求的
• 非遮挡物(z > depth)的深度值均值，这是未知量

假设区域内非遮挡物纹素有个，遮挡物纹素有个，一共有个纹素，那么有下式： 接下来，我们近似 这里用到切比雪夫不等式。

那么接下来只要知道就能求出了。这里直接大胆近似，让，因为大部分阴影被平面所接收。

背后的算法

给定SM，如何快速求出在指定矩形范围内的深度值均值？

• 如果矩形是正方形，可以用Mipmap来进行范围查询：

  它快速、近似地查询结果，由于结果可能是插值生成的，不是很精确。

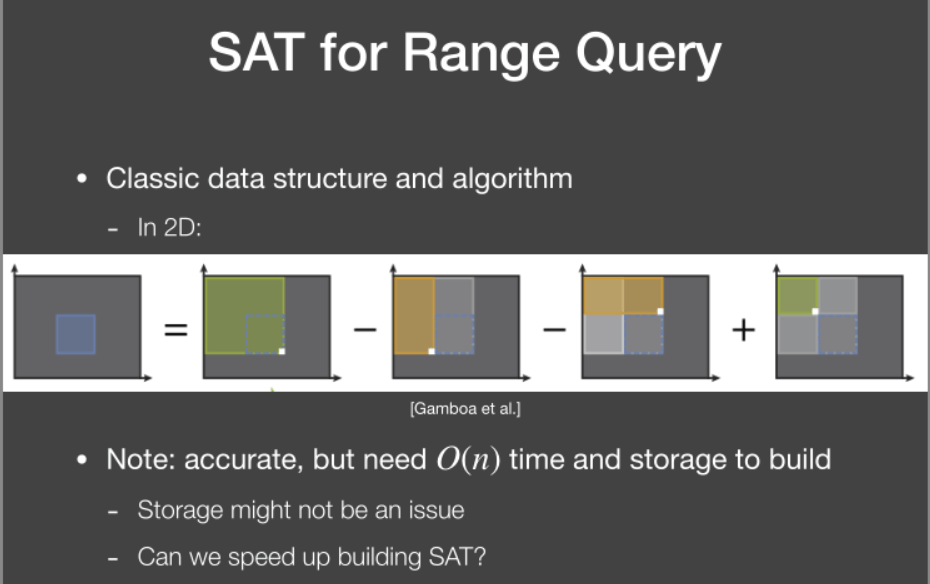
• 更通用的情况是使用SAT进行范围查询，它就是 二维前缀和：

  但在构造前缀和时需要花费时间，如何加速？行间/列间可以并行计算（GPU，CUDA……）

缺点

VSSM的缺点在于它没有使用具体的分布，当分布过于简单时，计算结果不正确（过亮/过暗）。

MSM

目标

相对于VSSM，使用一个更准确的分布去描述阴影，并且消耗的存储量也不大。

思路

使用高阶的矩(moment)去描述分布，一般4阶矩就够用。

矩：就是某数的n次方，例如VSSM就只用了前2阶。

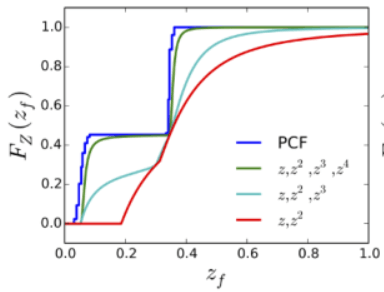
优缺点

优点：效果很好。

缺点：存储量大，性能较差（用4阶矩重建CDF）。

参考资料

• GAMES202: 高质量实时渲染 (ucsb.edu)