本文复习一下Shadow Map是怎么做的，它的问题与解决方法，以及他背后的数学。

简要回顾

首先对在GAMES101学过的Shadow Map

是两个Pass的算法

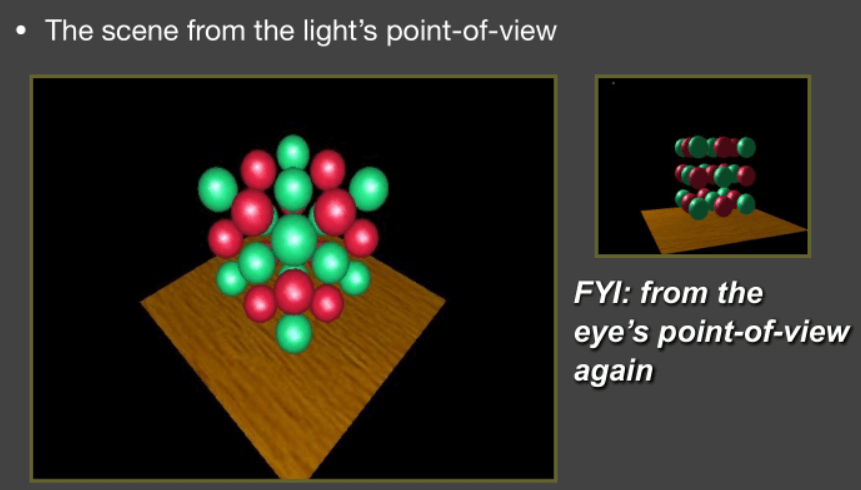
1. 从光源看向物体，生成它的SM（Shadow Map）

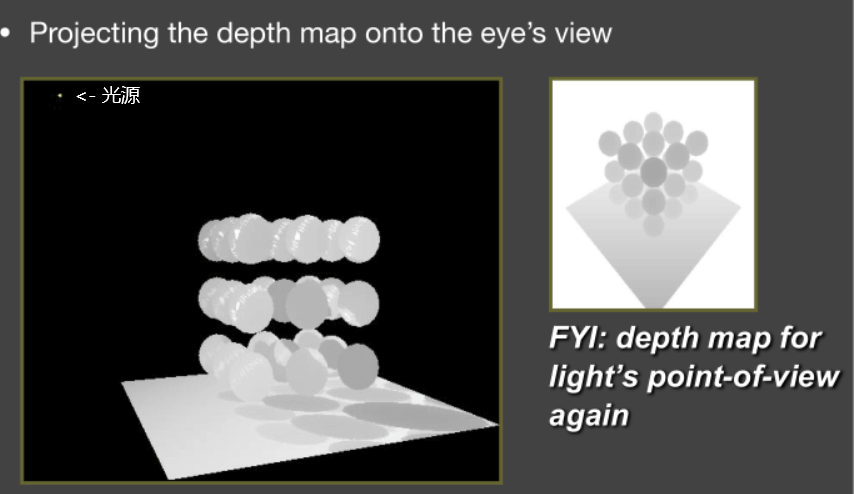
2. 从摄像机看向物体，使用之前生成的SM做比对，在确定是阴影的地方生成阴影。

是图像空间的算法

优点：要得到阴影仅需SM，而不需要场景中物体的几何信息。

缺点：有自遮挡和走样问题。

存在的问题

自遮挡现象(Self Occlusion)

Shadow Map会出现自遮挡现象，由数值精度问题造成。

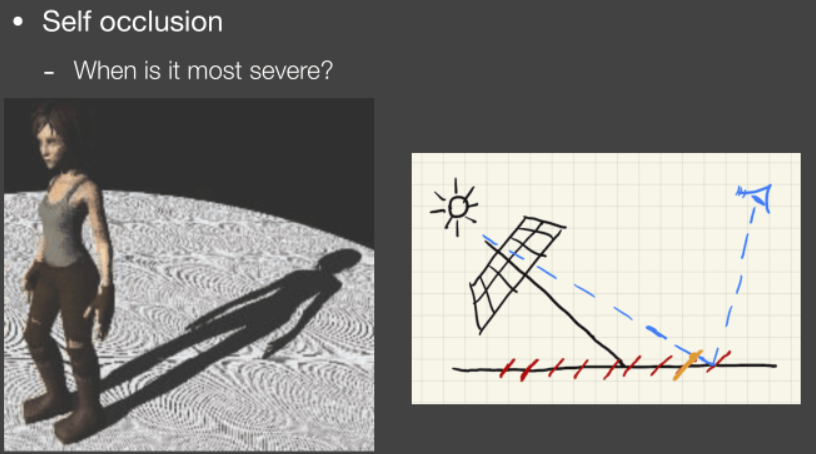
如图，在SM中，每个纹素记录一个深度值，它不是连续的，导致当我们看向某物体，结果应该是蓝红交点，但被前面的黄蓝交点挡住了，产生自遮挡现象。

可以通过 添加偏移量(bias) 的方法解决该问题，并且该偏移量可随光源与地板的角度变化（越垂直越小）。

阴影悬浮(Detached Shadow)

引入偏移量后，发生“阴影悬浮”问题，也称彼得潘问题。

由于偏移量过大，导致一些本来是阴影的像素点变得不再是阴影。解决方法有许多，这里介绍一下工业界和学术界是怎么解决的：

• 工业界：挑一个合适的偏移值；采用正面剔除，降低物体深度以减小偏移值的影响。

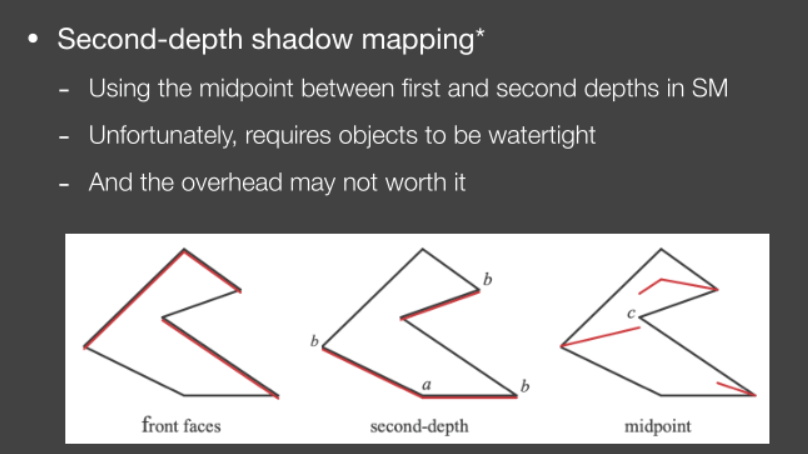
• 学术界：使用次小的SM（second-depth SM）。

  如图，进行两次SM的Pass，记录遮挡物最小和次小的深度值，然后去中位数参与后续过程。这个方法的缺点是，要求物体必须是有厚度的(watertight)，而且运算速度较慢。

走样问题

使用SM生成的阴影还会有走样问题，阴影的精细程度受SM贴图的分辨率限制。

可以使用Cascade SM，PCF等方法缓解走样问题。

背后的数学

在RTR领域中，常拿不等式作为“约等式”使用。因为RTR领域中更关心近似相等：

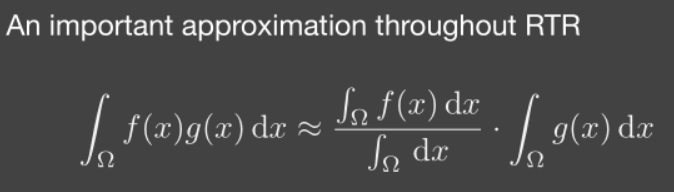
其中，那个分母是归一化常数。当 积分范围较小或被积函数足够光滑 时，近似值更准确。

在SM中的应用

首先回顾渲染方程，在RTR领域中的渲染方程如下：

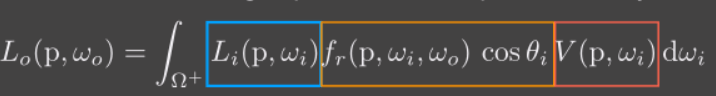
分为间接光，BRDF和可见性三部分。这里使用上边的约等式，将 可见性和剩余两部分分离出来：

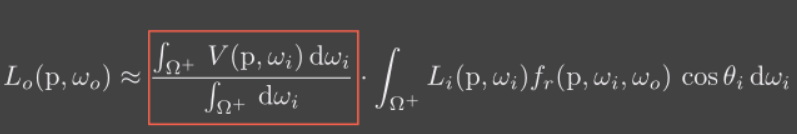
现在就有可见性和着色结果两部分了，这正是SM所做的事，根据可见性决定是否有着色结果。

什么时候用更准确？

1. 积分范围较小时（即平行光，点光源）
2. 着色结果足够光滑时（diffuse BSDF，光源平滑）

参考资料

• GAMES202: 高质量实时渲染 (ucsb.edu)