这篇文章着重补充上一篇文章中的一些数学原理，如粒子模拟，求解常微分方程等。

单粒子模拟

速度场（Velocity Field）：类似光场、磁场，在任意时刻t和位置x，有对应的速度取值 v（x，t）。

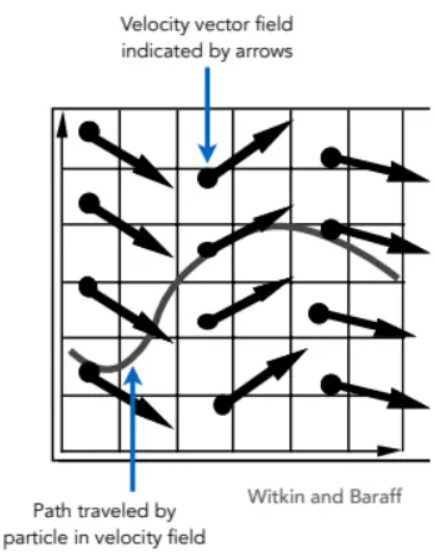
求解某个时刻粒子的位置实际上是求解常微分方程(ODE)：

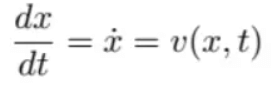
欧拉方法

可以使用欧拉方法来求解上边提到的常微分方程，它通过时间间隔来求解某时间的位置和速度：

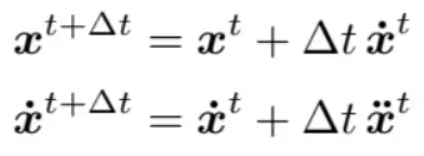
PS：

1. 右上角的不是几次方，而是角标，代表t时刻的xxx

2. 这里用的是显式/前向欧拉方法

使用欧拉方法计算常微分方程时会出现误差，而且误差会越来越大，因为它以前一次计算结果为准。当步长 越大，误差就越大：

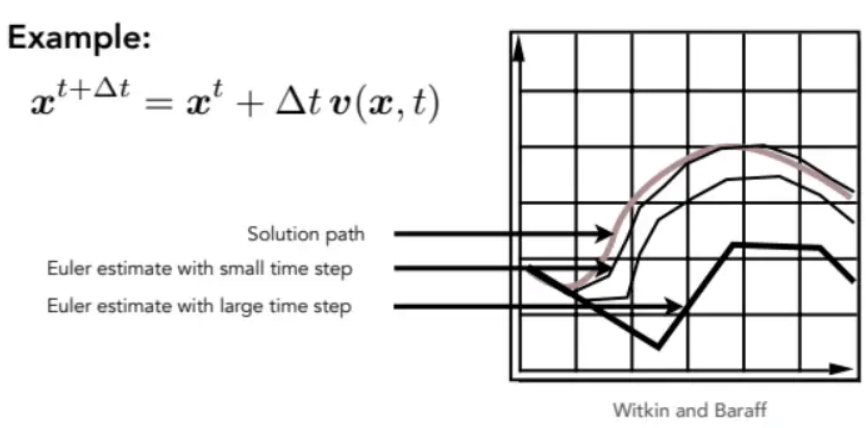
对于误差，在模拟中会产生错误，但是在渲染中其实并不太在意这种误差。

使用欧拉方法计算ODE时也有 不稳定性 。例如面对螺旋状的速度场，粒子本应一直在这个场里边，但使用该方法会导致错误被一步步放大，最终使粒子走出速度场。这和信号与系统里的“正反馈”差不多。

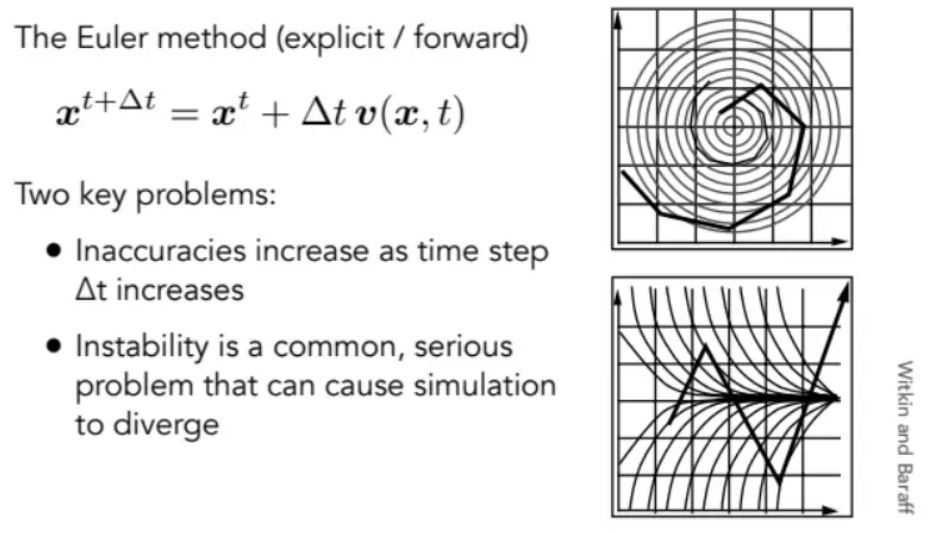
对于不稳定性，可能会加剧错误，在模拟中不能被忽视。

改善欧拉方法的不稳定性

有若干种方法可以改善欧拉方法求解ODE的不稳定性。

中点法

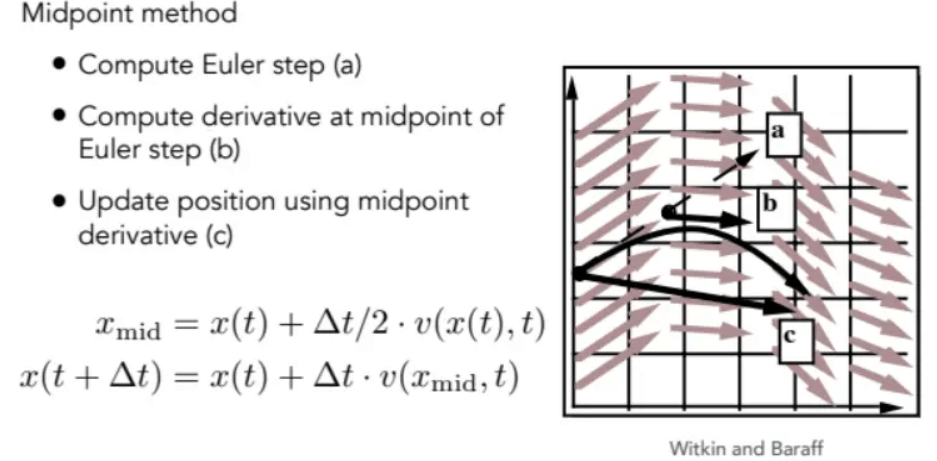
1. 用欧拉方法计算出 a 点
2. 计算 a 点与初始点的中点的速度（位移的导数）
3. 利用这个点的速度去更新初始点位置

中点法多了一个二次项，所以更加准确：

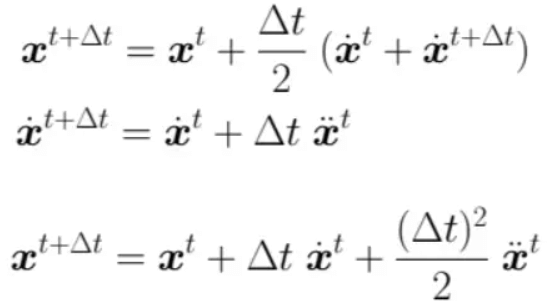
自适应步长法

在中点法的基础上，通过进行二次验算，判断是否要将步长缩短以减小误差。步骤如下：

1. 用一次欧拉方法计算
2. 用一次中点法计算
3. 计算
4. 如果结果大于阈值，说明误差过大，应减小步长再算一次。

隐式/后向欧拉方法

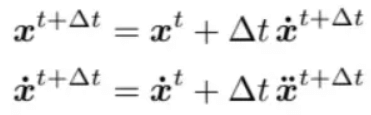
• 使用欧拉公式时永远都使用下一个时间的速度与加速度
• 求解的时候并不好求，需要使用寻根算法如牛顿法
• 可以提供比较好的稳定性

龙格库塔系列方法(Runge-Kutta Families)

龙格库塔系列的方法擅长解常微分方程(ODE)，特别是非线性方程情形。其中RK4（四阶）方法用的最多。

基于位置的方法/Verlet积分

优点：快速且简单

缺点：不是基于物理的，能量不守恒

刚体模拟

刚体模拟（Rigid body simulation），刚体，不会发生形变，即内部都会以一种方式（趋势）进行运动，所以也可以把刚体模拟看成是单粒子模拟的扩充：

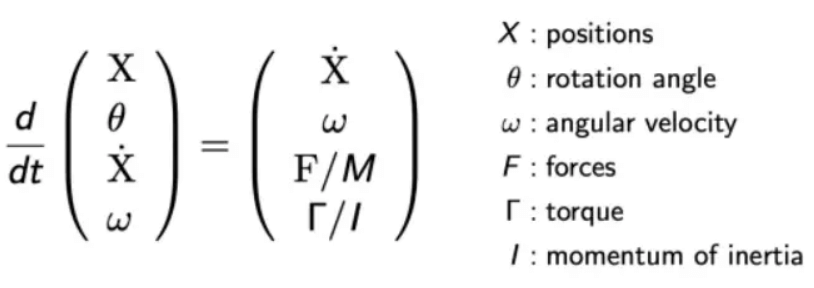
流体模拟

一种简易流体模拟（Fluid Simulation）的方法：

• 假设水体由许多不可压缩的刚体小球组成
• 由于水不能被压缩，只要某处的密度发生了变化，就应该通过改变粒子的位置来“修正”
• 为了修正，要知道一个小球位置的变化对其周围小球密度的影响，即任何一个点的密度梯度(导数)
• 修正位置的过程是一个梯度下降的过程

这样简单的模拟最后会一直运动停不下来，我们可以人为加入一些能量损失。

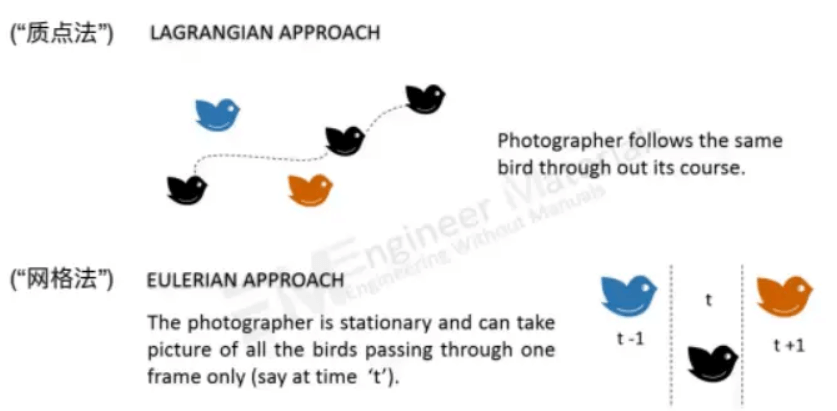
模拟像流体这样大量物体的运动，有两种思路：

• 拉格朗日质点法：以每个粒子为单位进行模拟

• 欧拉网格法：以网格为单位进行分割模拟

• 物质点方法（MPM）：当然，也能将两种方法综合起来（粒子将材质属性传递给网格，模拟的过程在网格里做，然后把结果插值回粒子），以吸收他俩的优点。

参考资料

• GAMES101-现代计算机图形学入门

• 22 动画与模拟（求解常微分方程，刚体与流体） (yuque.com)