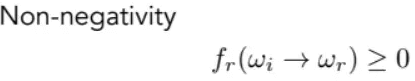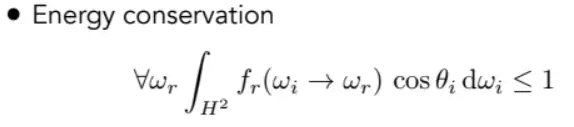阅读这篇文章可以了解到：

• 材质与BRDF的关系
• 一些微表面理论
• 材质的区分
• BRDF的性质和测量等

什么是材质(material)

自然界的材质：丝绸、头发等各种各样的物体表面。

图形学中的材质：给物体指定某种材质，该材质和光线作用后所得到的正确渲染结果（表面部分）。

观察渲染方程，发现BRDF项决定光如何被反射，因此认为 材质就是BRDF 。

简单材质(BRDF)

漫反射材质(BRDF)

漫反射材质(Diffuse/Lambertian Material)，光线打到一个点上后均匀反射到不同方向上。

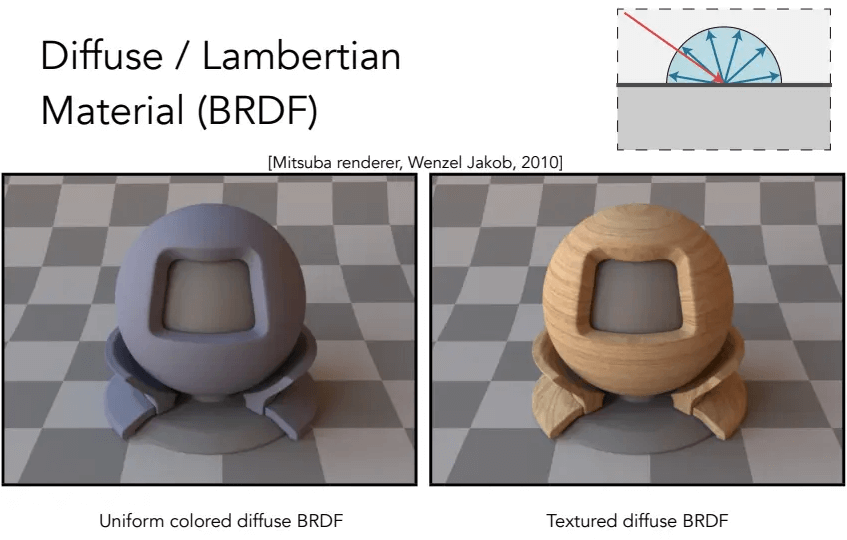
学了渲染方程后，可以研究一下 漫反射系数 的含义了：

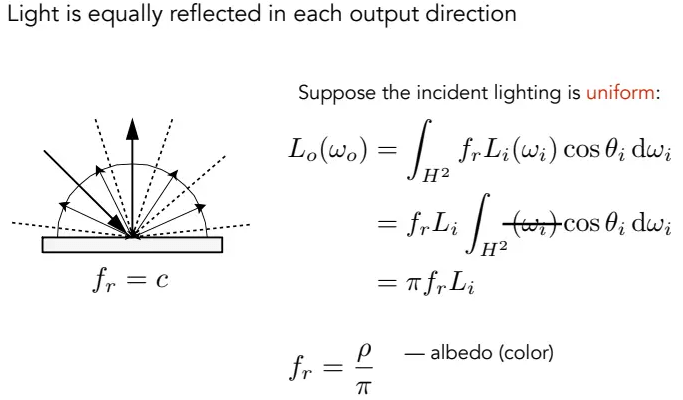
假设入射光和反射光都是均匀分布的，那么有。在上图的渲染方程（忽略自发光项）中，将常数项移出去，剩下对半球的积分，计算并消去，可以得到漫反射系数，此时着色点完全不吸收入射光的能量。

定义 反射率(albedo) 为，可以是单通道的一个值，也能是RGB，还可以是光谱。值的范围在，那么漫反射系数的范围就是.

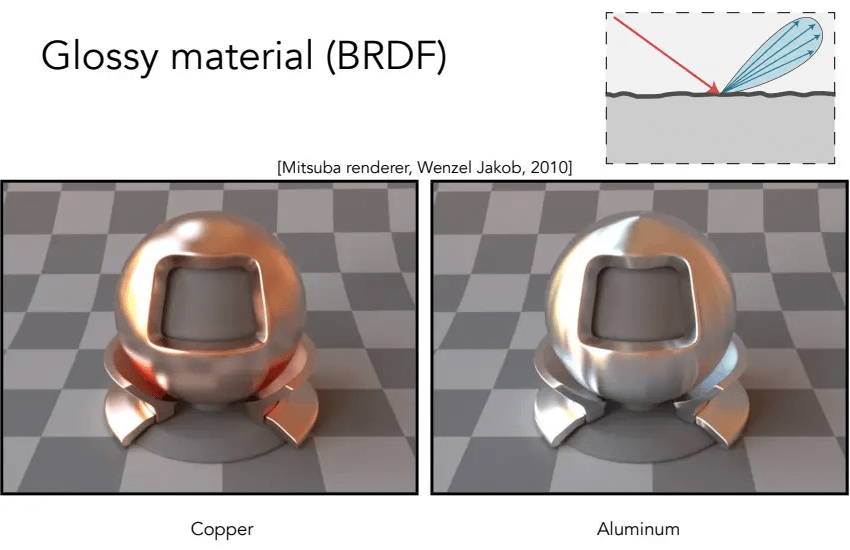
光泽材质(BRDF)

光泽材质(Glossy)，不完全进行镜面反射，跟金属一样：

散射材质(BSDF)

光线打到某点，会发生反射(reflective)和折射(refractive)，常见的材质有玻璃和水等：

反射BRDF和折射BTDF共同称为散射BSDF，S指的是散射。

反射材质(BRDF)

这是完美的镜面反射。

反射定律

反射材质遵循光的反射定律：

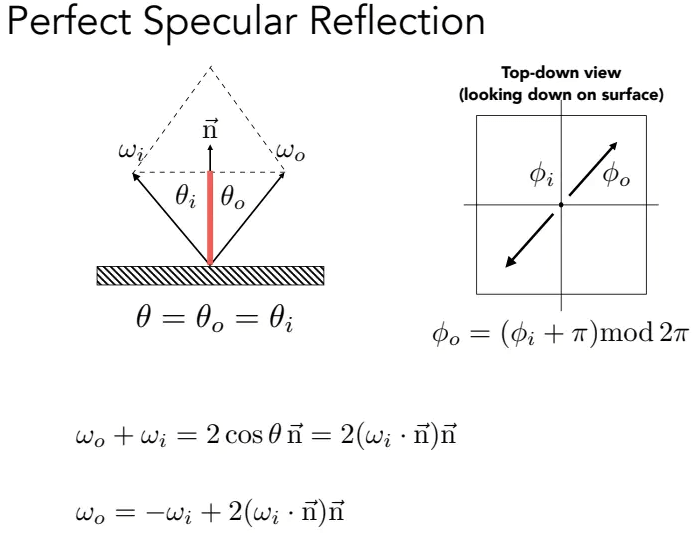
如左图，可以通过角平分线等于光线在其上投影的2倍，推导出反射光关于入射光的关系式。如右图，也能从上往下俯视，由于入射光和反射光他俩在方位角的朝向正好相反，可以找到他俩方位角的关系式。

反射材质的BRDF可以用Delta函数来描述，待补充。。。

折射材质(BTDF)

折射不是BRDF而是BTDF，T是折射(Transmit)。

斯涅尔折射定律

给定入射方向和法线，如何计算折射方向？这得用到 斯涅尔折射定律(Snell’s Law)。

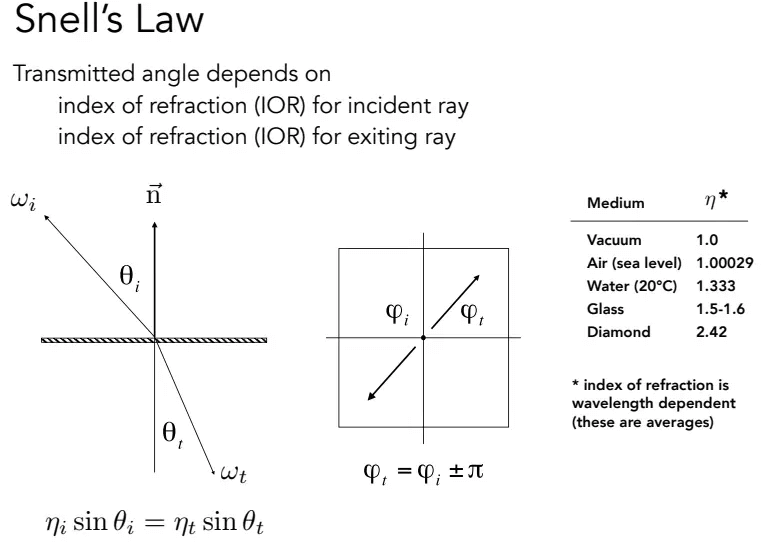
可以先计算出入射角，然后将两个介质的折射率（常用折射率在右边）带入公式，即可得到折射角。也可以俯视看，它俩的方向角正好是相反的。

算好的折射角余弦如下： 从上式可以看出，当时，无法发生折射，即发生全反射现象。例如下图，人在水底下看，只能看到一个锥形区域。

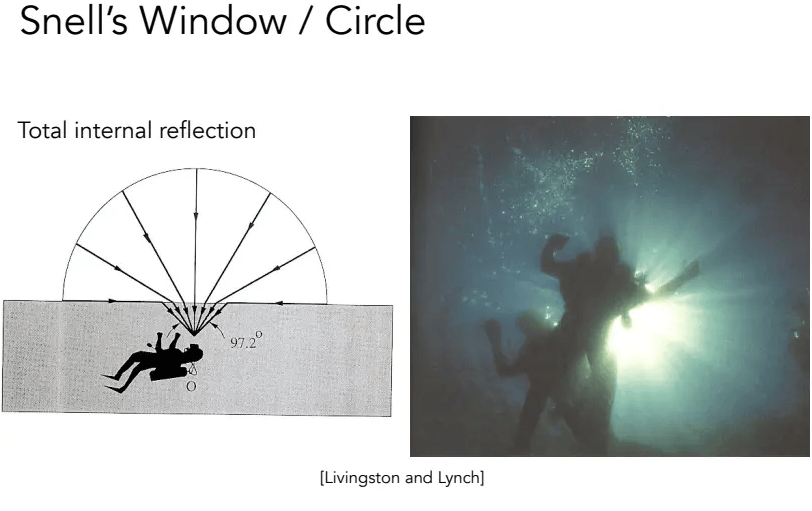
菲涅尔项(Fresnel Reflection/Term)

反射率取决于观察角度（和光的偏振/极化），例如下图，随着观察角度（法线和视线的夹角）增大，桌面上反射物体就越清楚：

绝缘体的菲涅尔项

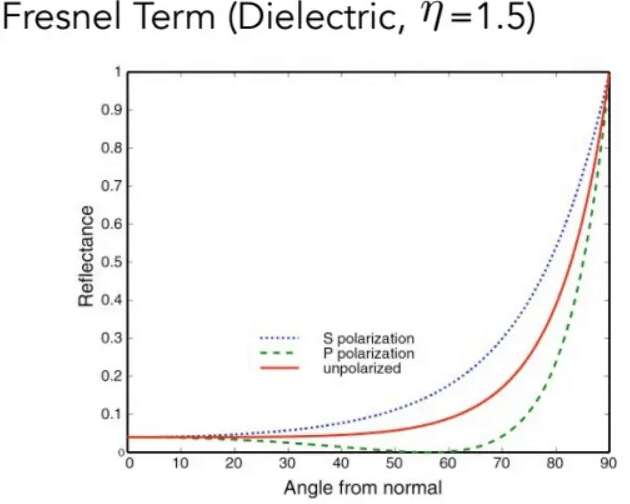
导体(金属)的菲涅尔项

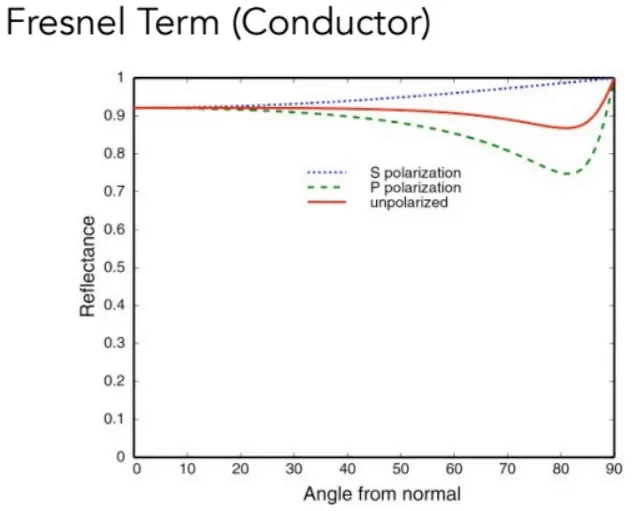
计算

微表面模型

微表面模型(Microfacet Material)，是一种基于物理的材质。假设离某物体足够远，看不到它具体的细节，但这些细节又会影响物体表面整体的渲染效果。

例如一个粗糙表面(Rough Surface)：

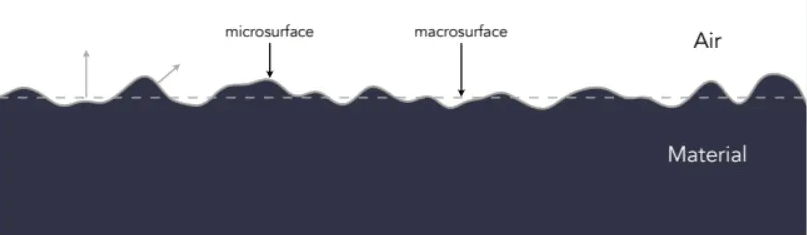
在宏观(Macroscale，就是虚线部分)层次，这是个平坦且粗糙的表面；在微观(Microscale)层次，这是个凹凸不平但有着完美镜面反射的表面。也就是说，从远处看到的是材质，从近处看到的就是各种各样的几何（离远了会消失变成材质）。

微表面BRDF的核心是 微表面法向量的分布，每个微表面都有自己的法向量，它们的分布对整体表面的法向量有贡献。

例如有光泽的表面法向量分布较为集中，粗糙的表面法向量分布较为分散：

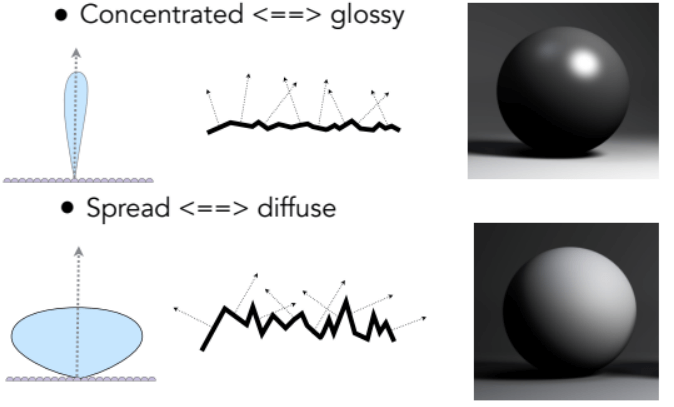
计算微表面BRDF的公式如下：

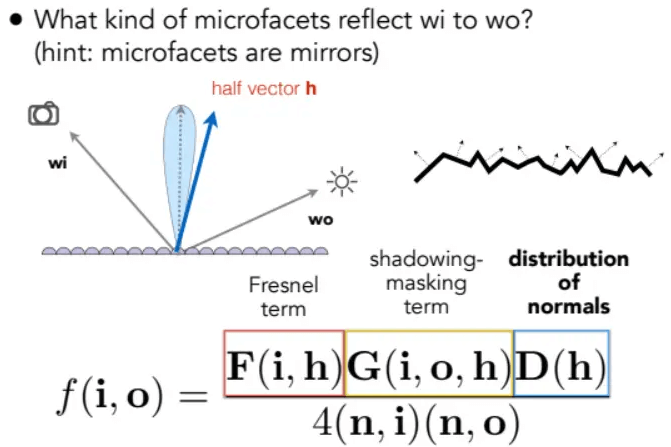
• F(i, h)：菲涅尔方程(Fresnel Rquation)，描述了物体表面在不同入射光角度下反射光线所占的比率

• G(i, o, h)：几何函数(Geometry Function)，描述了微平面自遮挡的属性。一个微平面可能会挡住其他微平面，从而减少表面反射的光线。

  PS：当光线几乎是平着射进来时（成为Grazing Angle），此现象容易发生，该项就是用来修正它的（shadowing-masking）。

• D(h)：法线分布函数 （Normal Distribution Function），其代表了所有微观角度下微小镜面法线的分布情况。当微表面的法向量跟半程向量方向完全一致时，入射光才能反射出去。

区分材质

材质可以分为两类：

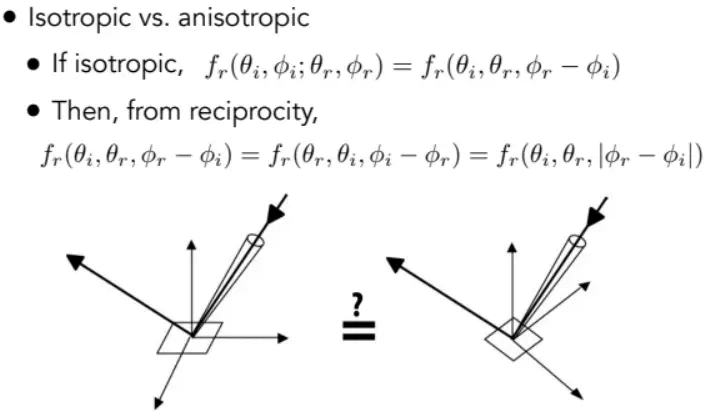
• 各项同性材质(Isotropic Materials/BRDFs)，微表面不存在方向性，或方向性很弱，即微表面法线分布均匀。
• 各向异性材质(Anisotropic Materials/BRDFs)，微表面法线分布有明确的方向性。

可以利用绝对方向角区分他俩，如果它的BRDF满足：

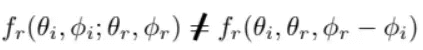
那么就是各项异性材质。

BRDFs的性质

• 非负性，能量不是非负的

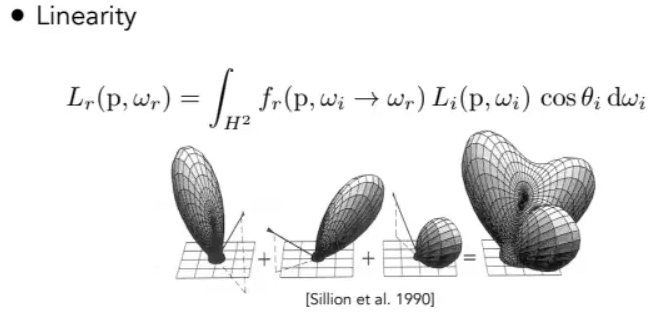
• 线性，例如Blinn-Phong模型，BRDF可以拆成很多快，然后加起来求和就行。

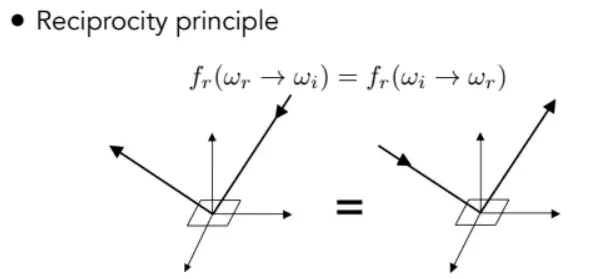
• 可逆性，交换入射方向和出射方向，结果一样

• 能量守恒

• 各向同性/异性

BRDFs的测量

测出来的BRDF是绝对准确的，因为计算出来的结果始终是模型而不是实体，而且能测出来就省去了计算。

如下图，测量BRDF的方法就是枚举camara和光源的所有入射和出射方向。

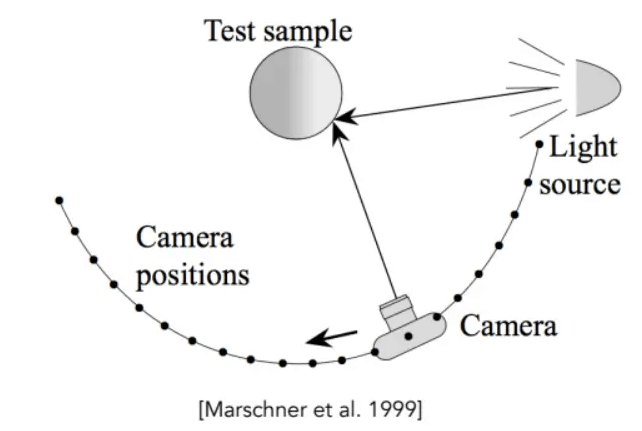
算法如下：

同时，可以利用BRDF的各向同性和可逆性等方法，来削减测量量。

有个著名的BRDF库，叫做MERL BRDF Database。

参考资料

• GAMES101-现代计算机图形学入门

• 17 材质与外观 (yuque.com)