03 - 辐射度量学&BRDF&渲染方程
之前对光强的定义仅有数字,而没有单位,这是不合适的。并且之前的whitted-style光追模型也不是正确的,因为它使用Blinn-Phong经验模型,不准确,且没有对漫反射的光线进行追踪。
因此引入辐射度量学。
辐射度量学(Radiometry)
辐射度量学是对光照的一套测量系统和单位,它能够准确的描述光线的物理性质。它定义了光的一些属性:辐射能量(Radiant energy),辐射通量(Radiant flux),辐射强度(Radiant intensity), 辐射照度 (irradiance),辐射亮度(radiance).
辐射能量&辐射通量(energy&flux)
辐射能量(Radiant energy)的定义:
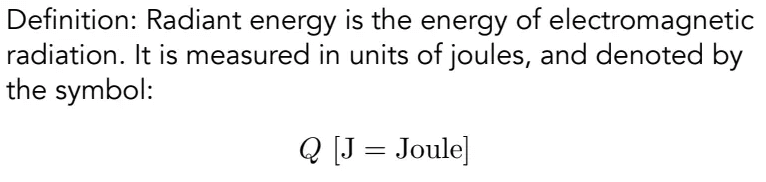
类似做功的大小,就是辐射出来的电磁能量,单位为焦耳。
辐射通量(Radiant flux)的定义:
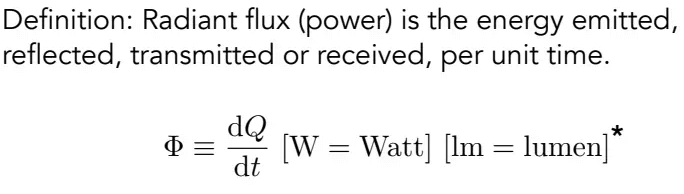
类似功率,就是在辐射能量的基础之上除以时间,也就是单位时间的能量。一般偏向用它来衡量光线的亮度,这时候单位是流明。
也能从另一个角度理解辐射通量,类似磁通量,辐射通量是一个单位时间内光子通过的数量:
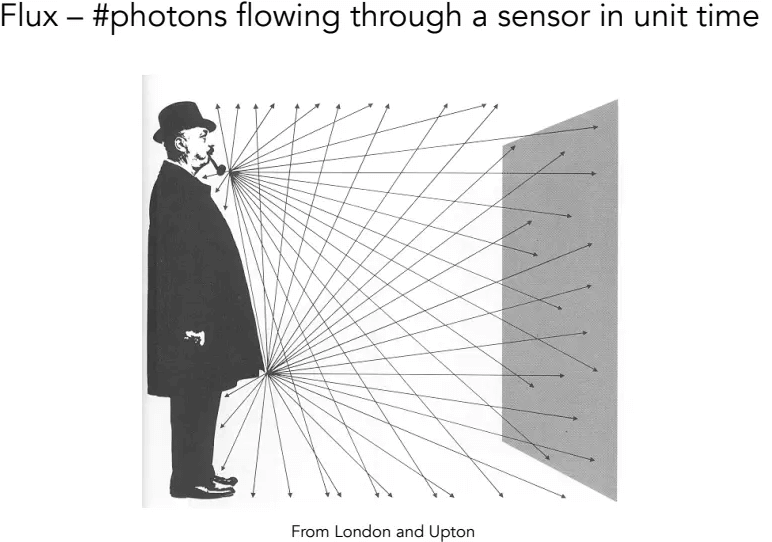
辐射强度(intensity)
定义
辐射强度(Radiant intensity),从光源发出的每单位立体角上的辐射通量/功率。
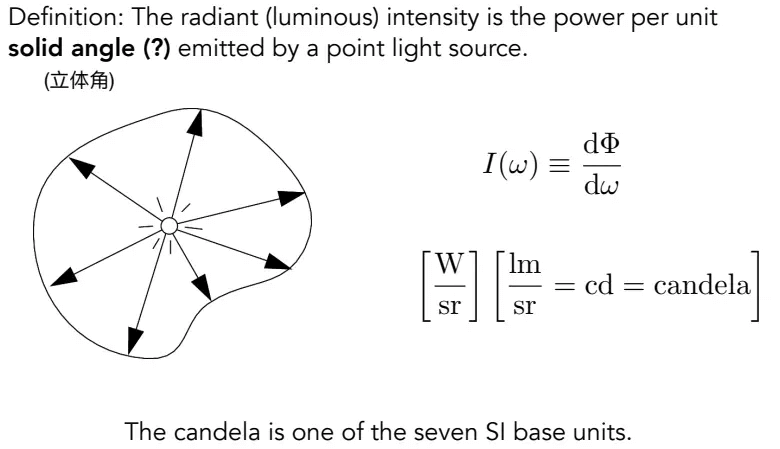
立体角
立体角是什么?可以从弧度角入手:
在2D中,我们有弧度角,计算公式如下:

在3D中,进行拓展便有了立体角:

因此,立体角就是球面上对应投影面积A和半径平方的比值,整个立体角为4
接下来,开始推导单位立体角
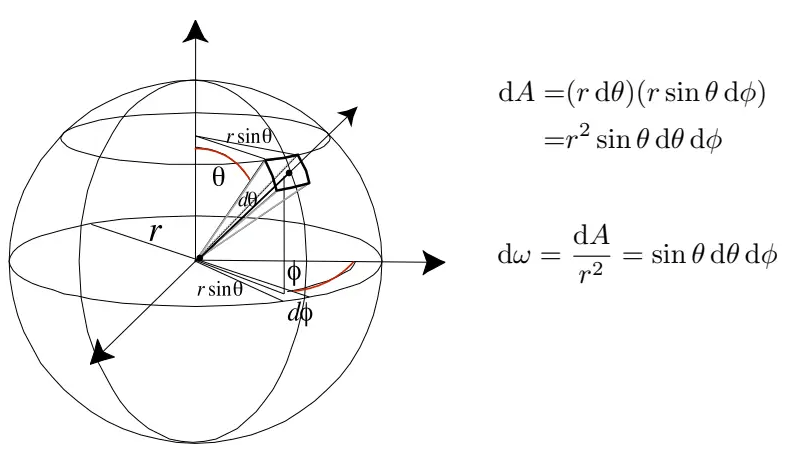
在球坐标系中,可以通过
也能验证一下,立体角最大是4
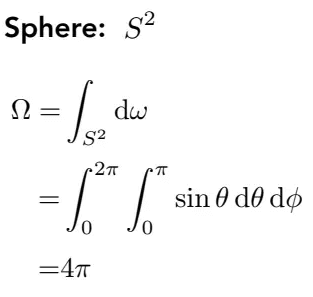
各向同性点光源的辐射强度
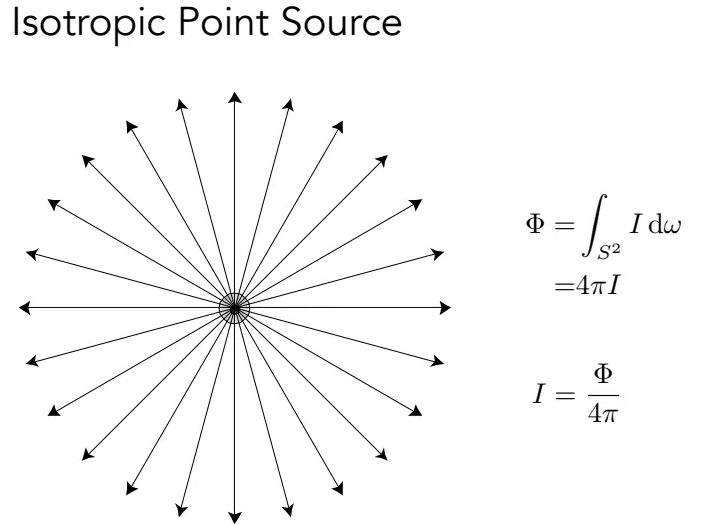
由于各项同性点光源所有方向上的亮度都与方向无关,立体角可以直接积分出来为4
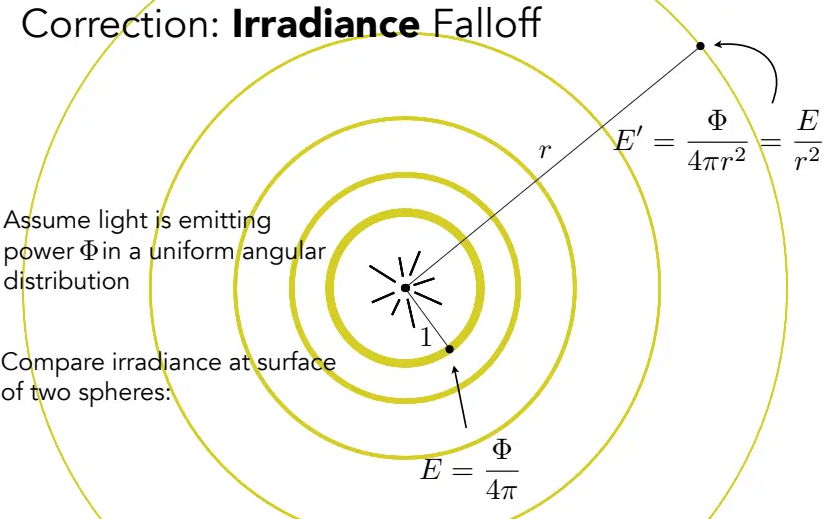
辐射照度 (irradiance)
辐射照度就是每单位照射面积所接收到的辐射通量/功率:

对于照射面积A,根据Lambert余弦法则,在计算时需要乘上
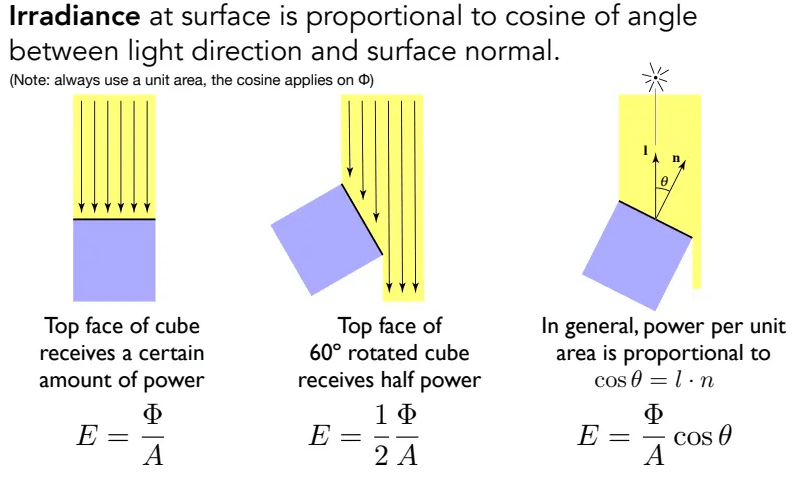
对于辐射通量/功率
辐射亮度(radiance)

辐射亮度就是指每单位立体角,每单位垂直面积的功率,很像是Intensity和irradiance的结合,它同时指定了光的方向与照射到的表面所接受到的亮度。可以从两个方面来考虑辐射亮度:
入射辐射亮度(Incident Radiance)

入射辐射亮度,就是指每单位立体角在表面的辐射照度,以一个很小的面。
出射辐射亮度

出射辐射亮度,就是指每单位垂直面积的辐射强度,以一个很小的范围。
和辐射照度(Irradiance)的区别

辐射亮度就是在辐射照度的基础上,增加了方向性,特指从某一方向
双向反射分布函数(BRDF)
从辐射度量学角度理解反射
可以从辐射度量学的角度去理解光线在某点的反射。一个微分小表面(
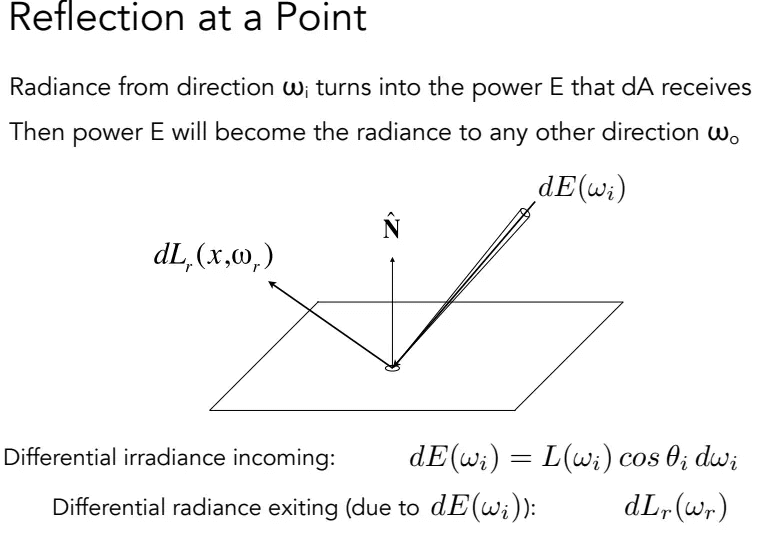
BRDF定义
而BRDF(Bidirectional Reflectance Distribution Function)就是一个描述有多少沿入射方向入射的光从表面朝出射方向反射出来的函数:
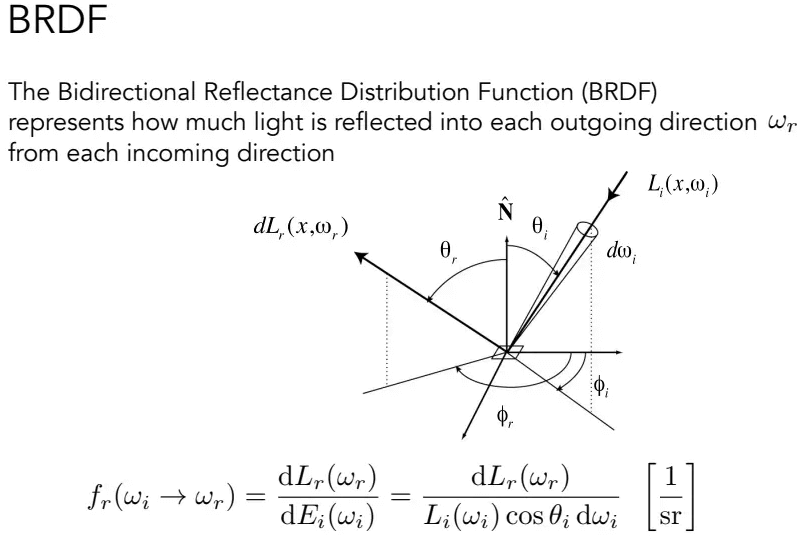
该函数有两个参数,入射光方向
反射方程
对
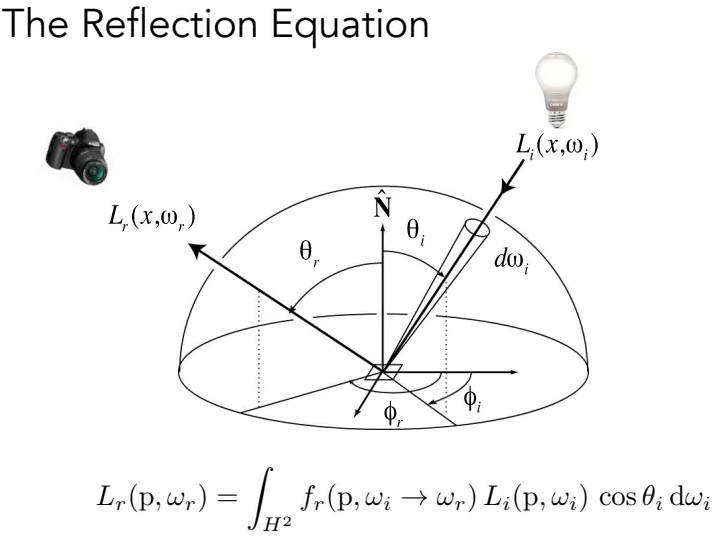
即任何一个着色点,在各个不同的光照环境下,由所有不同方向上入射光线的辐射照度贡献所得到的出射光线的辐射亮度之和。(麻了,这块还是有点理解不清楚)
但还有个问题,入射光线的辐射照度除了光源,还有可能是其他着色点反射光线的辐射亮度,即间接光照,因此这两个两的求法是递归的,很难解方程。
渲染方程(The Rendering Equation)
渲染方程只在反射方程的基础之上添加了一个自发光项(Emission term),这样就能通过一个方程去解释所有光:

其中,
理解渲染方程
首先是一个点光源和单个物体的反射方程:

然后是多个点光源和单个物体的反射方程,只需将多个光源的贡献求和即可:
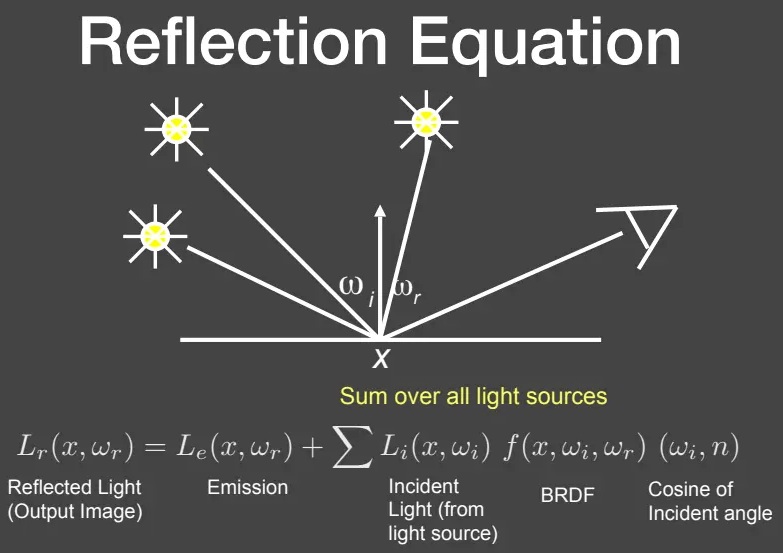
如果点光源变成了面光源该怎么办?面光源可以看成无穷多个点光源的集合,只需对面光源所在的立体角范围内进行积分,并确定不同立体角方向面光源入射光的辐射亮度即可:
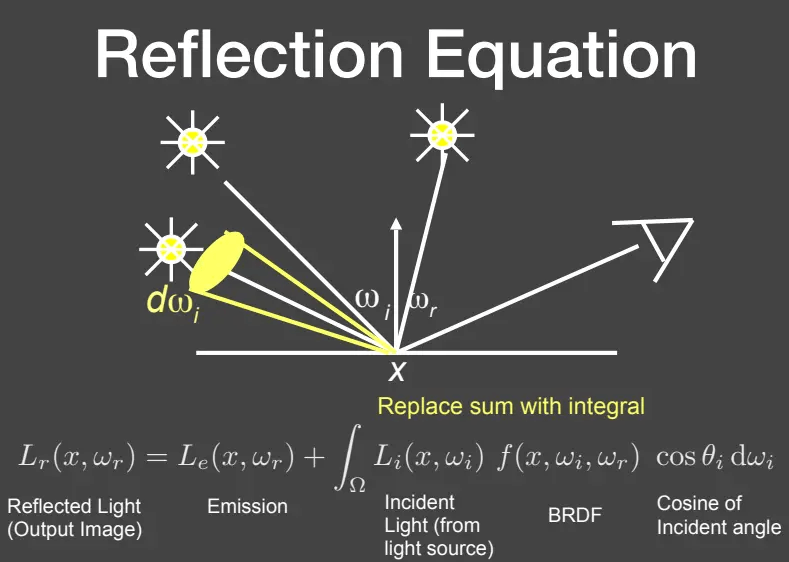
如果在场景中加入其他物体,使得物体之间发生光线交互后该怎么办?可以把其他物体也考虑成面光源,对光源所占立体角进行积分即可:
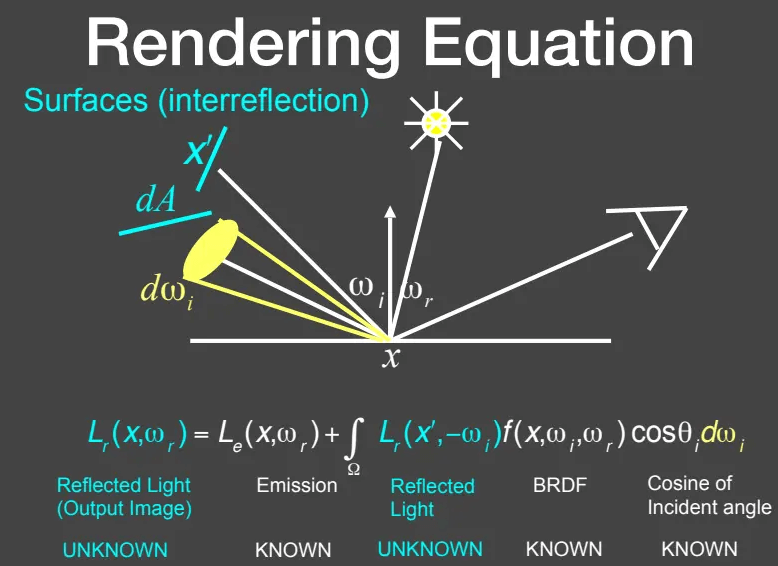
求解渲染方程
可以发现除了两个辐射亮度项,其他项都是已知的,那么就能简化为下式:

还能进行一些变换,将上式简化成离散的代数形式:

其中,L就是要求的反射光,E是自发光项,K是对光线进行反射的一种算子操作(由BRDF化来)。
接下来要利用线性代数的知识解出这个L:
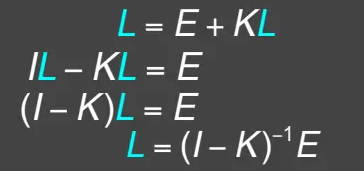
其中I是单位矩阵,再接着对
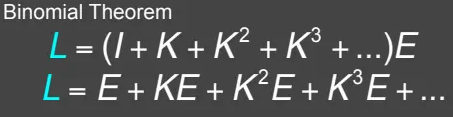
得到最后的式子,解释如下:
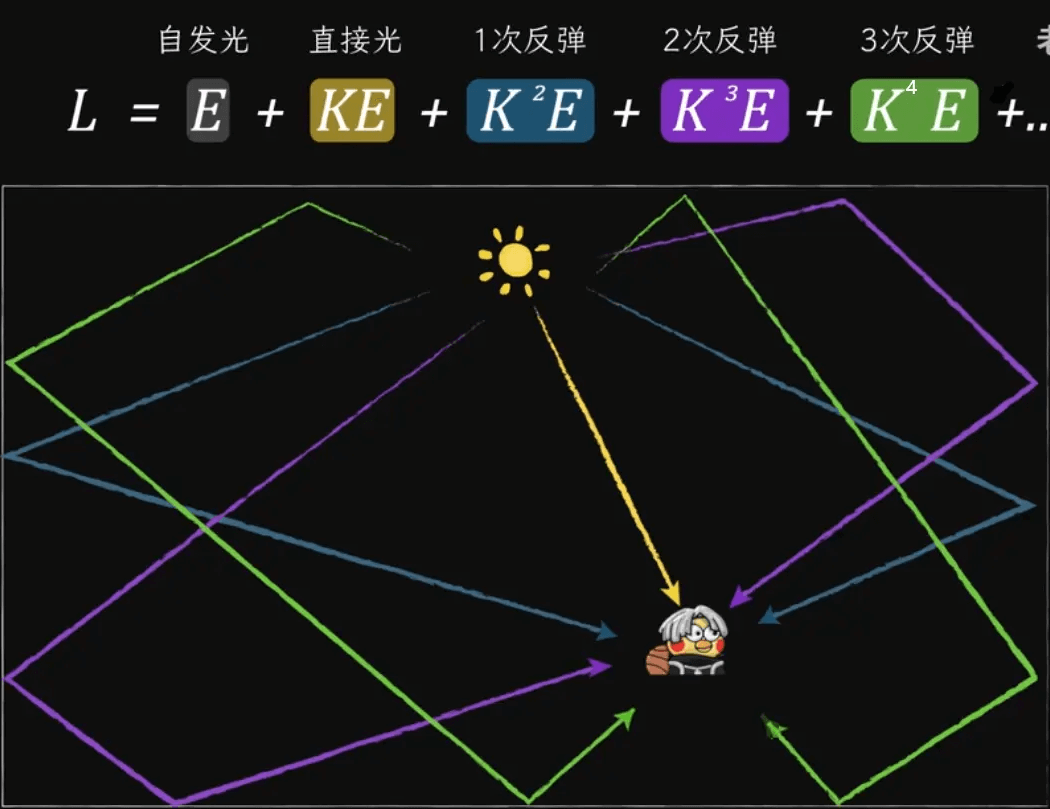
这些结果综合起来(自发光 + 直接光照 + 一定量的间接光照)就是全局光照,我们利用全局光照去逼近(肯定算不完,有n次弹射)渲染方程,从而得到最终效果。光栅化可以简单做的只有自发光和直接光,而光线追踪可以容易地做到后面的反弹光。
渲染结果
直接光照:

全局光照:



实际上,我们根本不需要一直计算反弹光,因为结果会在某次反弹后几乎无效果(收敛了),只需计算前几次就行。
参考资料
- GAMES101-现代计算机图形学入门
- 计算机图形学十四:基于物理渲染的基础知识(辐射度量学,BRDF和渲染方程) - 知乎 (zhihu.com)
- 【老奇】阴差阳错 撼动世界的游戏引擎_哔哩哔哩_bilibili,用动画形象解释了渲染方程!