02 - 曲线与曲面
贝塞尔曲线(Bézier Curve)
如图,蓝色的是贝塞尔曲线,起点是
de Casteljau算法
如图,有3个控制点,它将会画出2次贝塞尔曲线(n个控制点得到的是n-1次曲线):
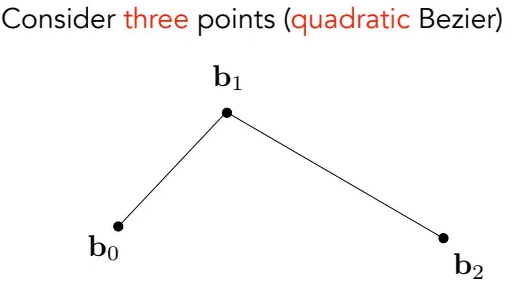
选定一个参数
如图,在
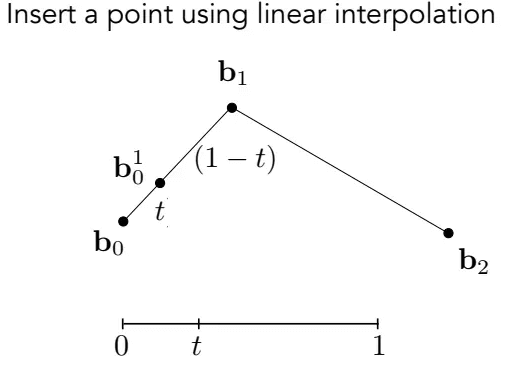
同理,在
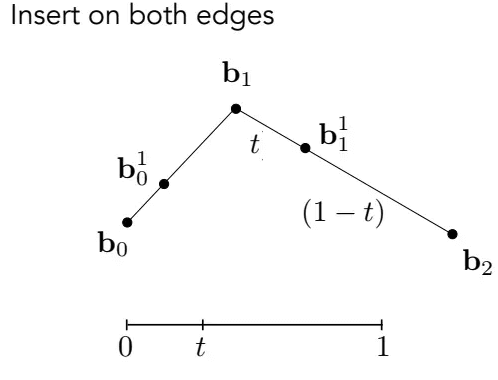
最后,连接这两个点,按同一个t再次进行线性插值,直到无法进行这样子的操作,这时候,得到的点就是贝塞尔曲线上,特定t对应的点:
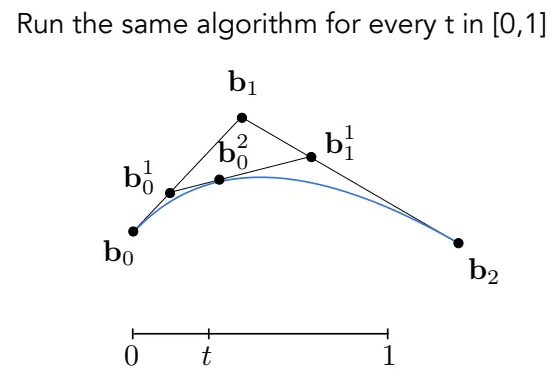
同理,4个控制点画出的三次贝塞尔曲线,其中一个点的确定过程如图:
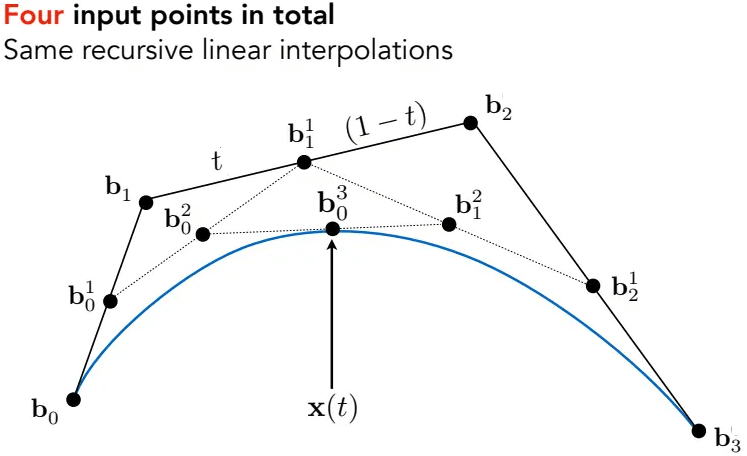
贝塞尔曲线方程
以3个控制点的2次贝塞尔曲线为例,取参数t,曲线上某点的方程如下:

可以发现,这是个关于t的二次方程,且系数有一些类似于二项式的规律,总结得到:

PS:
性质
必定经过起始与终止两个控制点
必定经与起始与终止线段相切
具有仿射变换性质,可以通过移动控制点移动整条曲线
凸包性质,曲线一定不会超出所有控制点构成的多边形范围
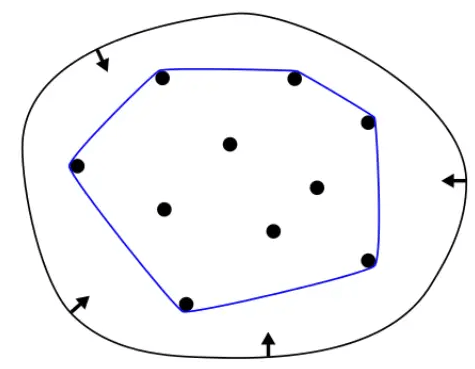
PS:什么是凸包(Convex Hull)?
能够包括给定的这些几何形体的最小的凸多边形就是凸包。
![]()
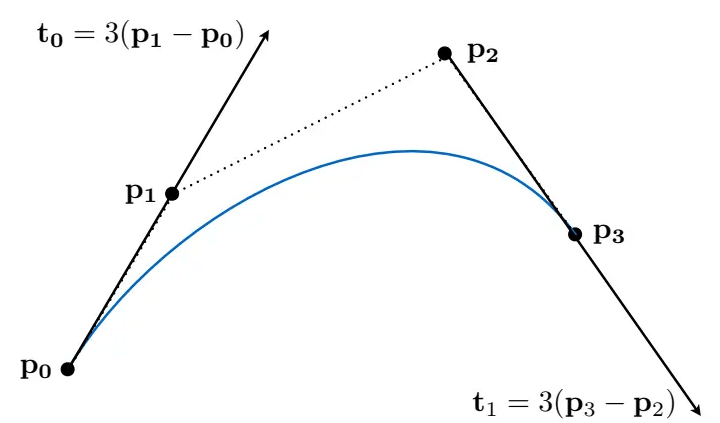
分段贝塞尔曲线
高阶贝塞尔曲线的控制点很多,很难控制局部的贝塞尔曲线形状:
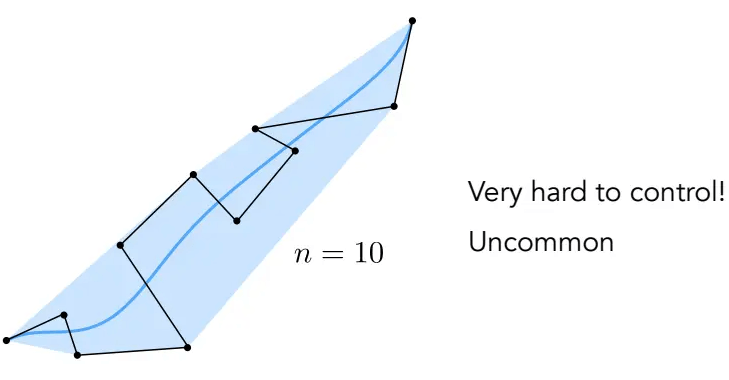
因此,可以进行分段处理,将一条高次曲线分成许多条低次曲线,然后连接起来。通常,低次曲线是3次的(4个控制点)。
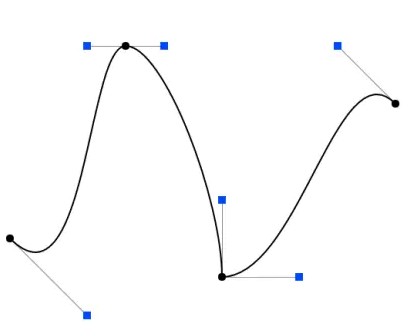
如果想要使得拼接的点看起来较为光滑的话,就要满足一些连续条件:
- C0连续:几何上连续,即前面曲线的终点和后面曲线的起点重合。
- C1连续:导数上连续,即满足C0后,前面曲线最后两个点距离和后面曲线最先两个点距离也要相同。
- C2连续:曲率上连续。
- …
还有贝塞尔曲线的升阶降阶等操作没说,待补充
(入门课,没说多少,待补充。参考清华大学-计算机图形学基础(国家级精品课)_哔哩哔哩_bilibili)
其他曲线
B-样条曲线(B-Spline)
样条曲线:

而B-样条曲线则通过基函数(各种各样的伯恩斯坦多项式组成)绘制而成,是贝塞尔曲线的扩展,它拥有比分段贝塞尔曲线更好的局部性。
NURBS曲线
NURBS曲线可以得到一些B样条曲线无法精准描述的圆锥曲线,如下图:
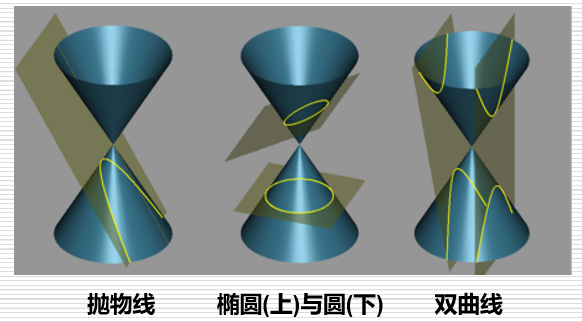
(入门课,没说多少,待补充。参考清华大学-计算机图形学基础(国家级精品课)_哔哩哔哩_bilibili)
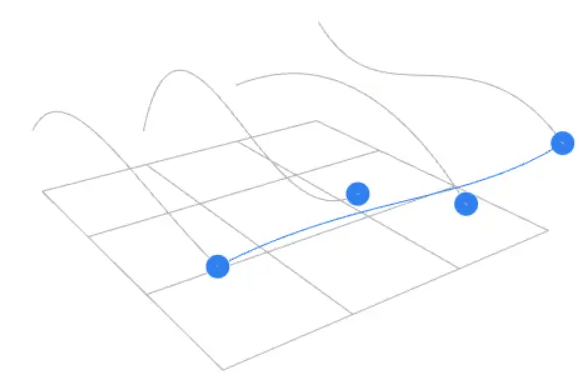
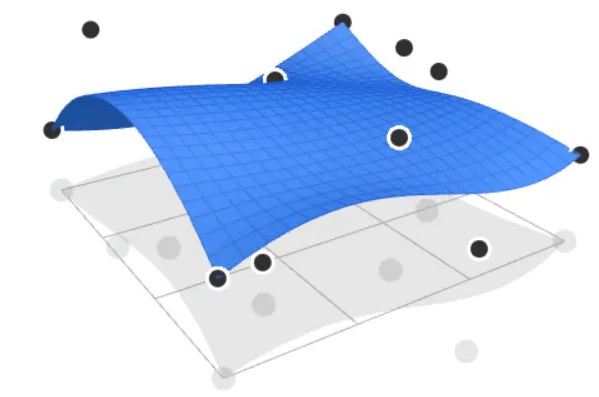
贝塞尔曲面
从二维拓展到三维,我们可以得到贝塞尔曲面:

接下来康康贝塞尔曲面生成的过程:
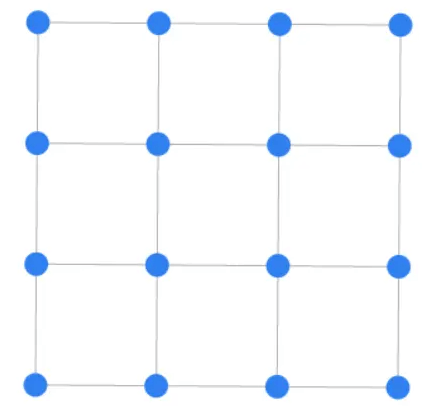
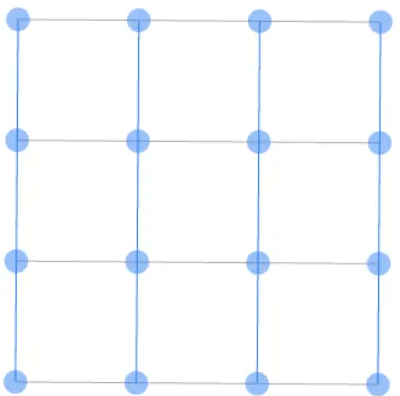
首先规定16个控制点,两个参数
。将点分为四组,一竖列一组,这是它们的俯视图: ![]()
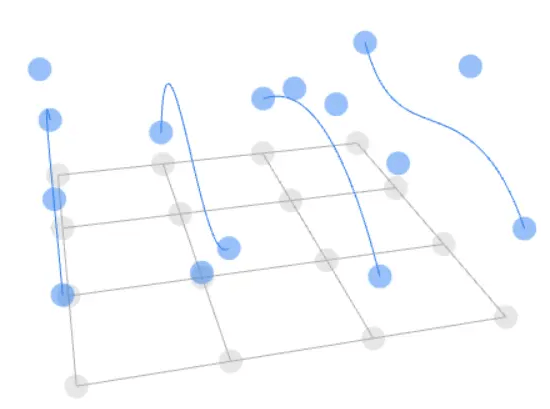
用第一个参数u和贝塞尔曲线的知识,得到每组生成的贝塞尔曲线:
![]()
换到正常视角是这样的:
![]()
在四条曲线上各取一点,形成一条贝塞尔曲线,再用第二个参数v,线动成面:
![]()
![]()
参考资料
- GAMES101-现代计算机图形学入门
- 计算机图形学十:贝塞尔曲线与贝塞尔曲面 - 知乎 (zhihu.com)