01 - 几何的基本表示
隐式几何(Implicit)
不清楚点的具体位置,只知道它们符合某个特定的关系。比如说球的隐式表示:
隐式几何的好处是 “很容易判断点在不在面上(带入点到式子中即可)”,坏处是“不直观,无法直接看出该方程表示什么曲面”。
表示方法
代数曲面(Algebraic Surfaces)
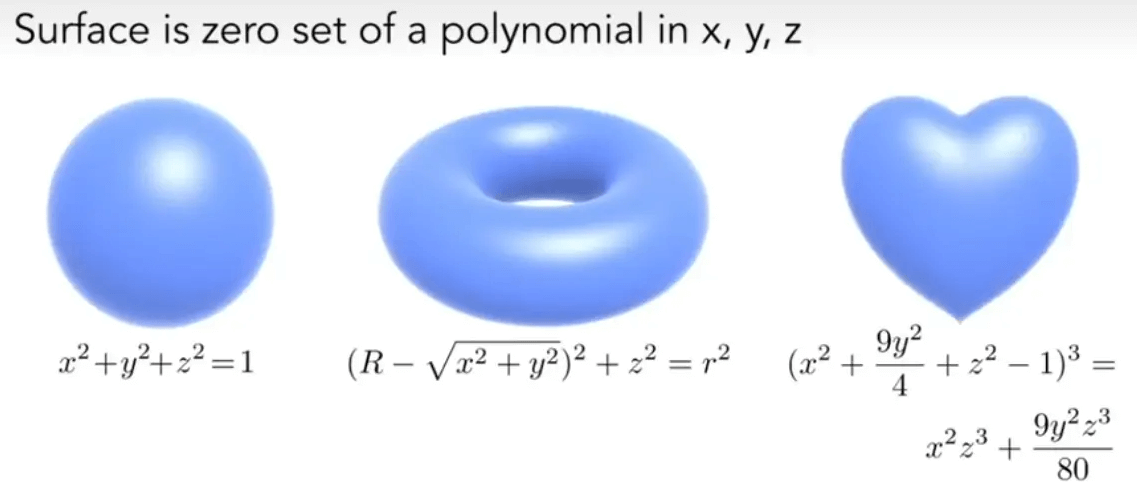
CSG(Constructive Solid Geometry)
通过对几种几何进行布尔运算,形成新的几何:
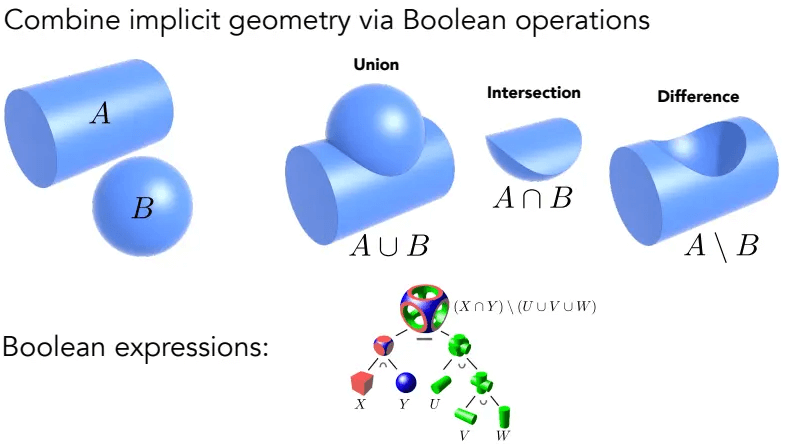
此方法广泛应用于各类建模软件中。
SDF(Signed Distance Function)
符号距离函数,也称距离场,描述空间中任意一个点到几何体表面的最短距离,到外表面为正,到内表面为负。如下图,将两个算好的SDF几何体通过融合(blending)操作得到:

这里解释以下SDF的用途,就是将两个及以上的物体边界“融合”起来,从而得到一个新的边界。例如,有两个阴影A和B,A占1/3,B占2/3,将其融合后得到的效果如下:
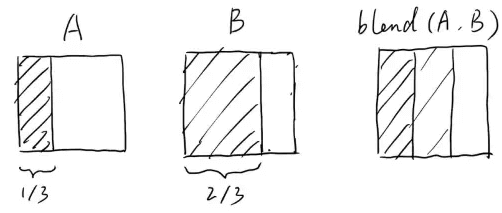
但是,这并不是我们期待的融合效果,应该将两个阴影的效果合起来,只有一个边界才对。这时候引入SDF,认为阴影的边界为0,左负右正,那么将这两个SDF加起来,可以得到融合后的效果(一个新边界):
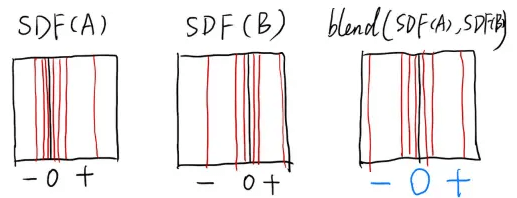
水平集(Level Set)
和SDF类似,也是找出函数值为0的地方作为曲线,但不像SDF会空间中的每一个点有一种严格的数学定义,而是对空间用一个个格子去近似一个函数,如下:
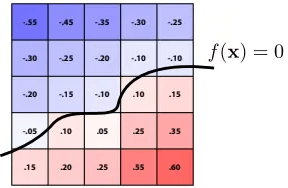
对该面内的每一个点利用已经定义好的格子值进行双线性插值就可以得到任意一点的函数值,并找出所有=0的点作为曲面。
该方法的好处是对于SDF,我们可以更加显示的区空间曲线的形状。该方法广泛的运用在医学成像和物理模拟之中。
分形(Fractal)
分型几何是指许多自相似的形体最终所组成的几何形状,和递归相似。

显式几何(Explicit)
所有曲面的点被直接给出,或者可以通过映射关系直接得到,如下图:
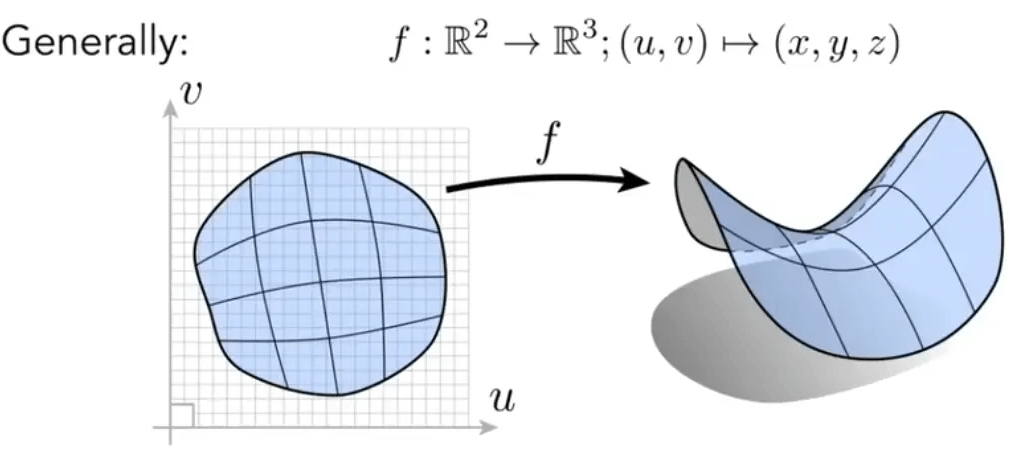
然没有直接给出点的数据x,y,z,但是拥有u,v的取值范围以及从
相对的,显式几何可以直观看出是什么曲面,但判断点是否在面上有些困难。
表示方法
点云(Point Cloud)
由很多很多点构成的的曲面,点多模型细节就多,点少模型细节就少。

多边形面(Polygon Mesh)
多边形面/网格,通过定义各个多边形面的顶点以及顶点之间的连接关系就可以得到许许多多的三角形面或是四边形面,再通过这些面来近似表现出我们想要的模型效果。

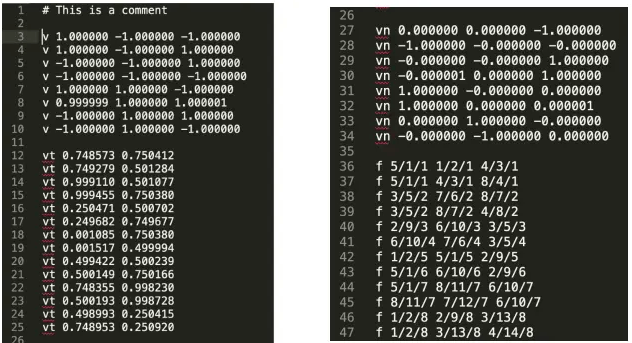
.obj文件用于图形学中,是一个文本文件,里边有物体的顶点信息,顶点纹理坐标信息,法线信息和它们的关联信息,f 代表一个面,其中x/x/x的第一位表示是哪个顶点,第二位表示该顶点纹理坐标是第几个,第三位表示法线信息是第几个。 3个 x/x/x表示3个顶点的信息构成一个面。
参考资料
- GAMES101-现代计算机图形学入门
- 计算机图形学九:隐式曲面(代数形式,CSG, 距离函数,分型几何)与显式曲面 - 知乎 (zhihu.com)