05 - 插值
重心坐标系(Barycentric coordinates)
重心坐标系主要用于三角形顶点上属性的插值。
数学定义
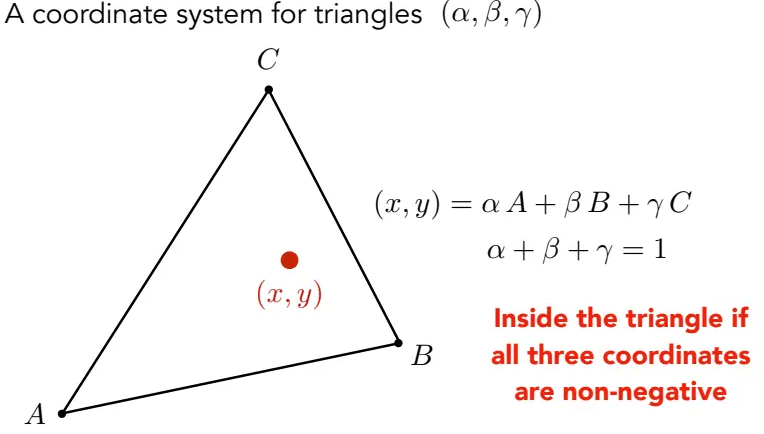
三角形ABC内任一点(x,y)都可以写成上图所示的三点坐标线性组合形式:
- 当
时,此时的点(x, y)即为三角形的重心坐标。 - 当
时,点在三角形内。
这三个值可以自成一个坐标系,就是重心坐标系
几何定义
重心坐标可以由面积比求出来:
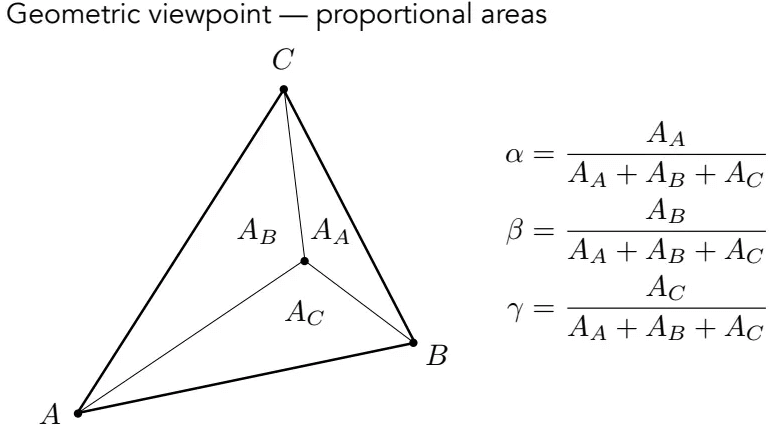
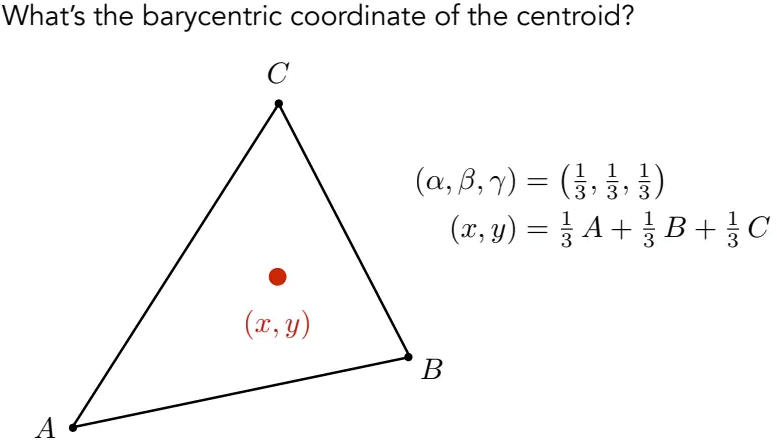
根据三角形重心的几何性质,它平分三个小三角形的面积,则重心的重心坐标为:
重心坐标公式
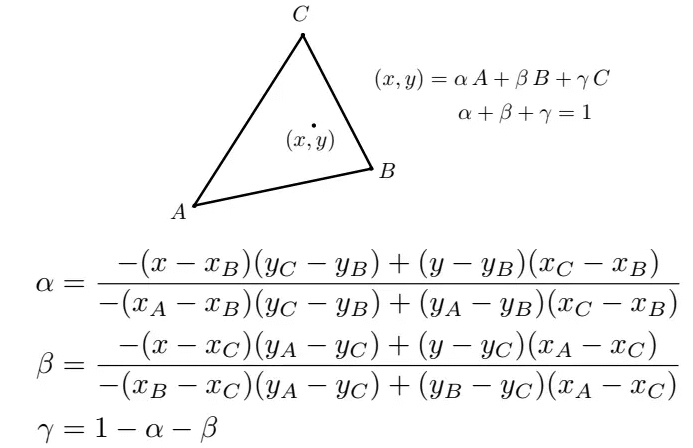
插值(interpolation)
为什么要插值?知道三角形顶点信息,需要在内部各个点之间做平滑过渡。
插值什么内容?纹理坐标,颜色,法向量等等…
重心坐标插值
插值
重心坐标可以用来插值,要插值的属性也得是重心坐标的形式
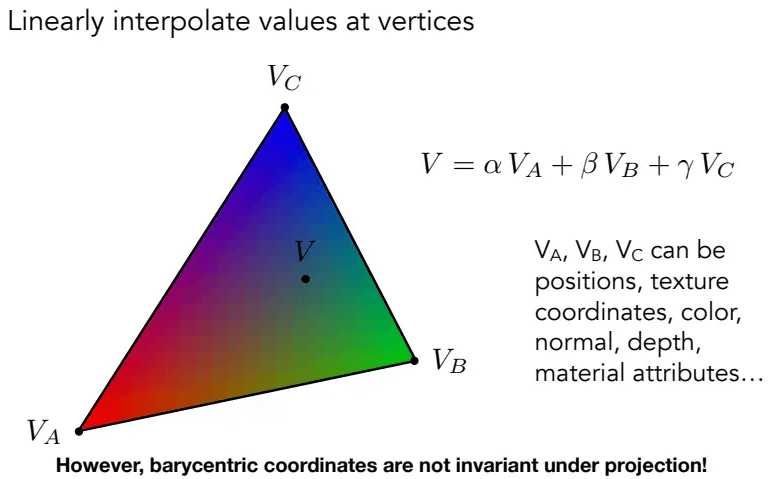
重心坐标虽然简单,但它在投影变换后会发生变化,因此三维空间中,先做好插值工作,然后才通过投影变换转换为二维空间。
透视矫正公式
(这里还是有点不懂哇)
推导过程详见这里,重心坐标插值下的透视矫正公式如下:
使用此公式前,还得知道内部点在 相机空间 的Z值
线性插值
线性插值待补充,双线性插值在纹理映射里有提到。
插值
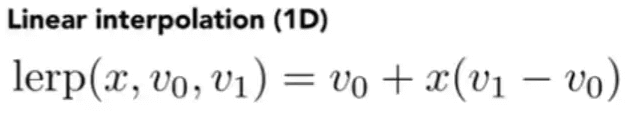
透视矫正公式
参考资料
- GAMES101-现代计算机图形学入门
- 计算机图形学六:透视矫正插值和图形渲染管线总结 - 知乎 (zhihu.com)
- 【重心坐标插值、透视矫正插值】原理以及用法见解(GAMES101深度测试部分讨论)_宗浩多捞的博客-CSDN博客