04 - 纹理映射
纹理映射(Texture Mapping)

看上面的球和地板,我们希望在某一物体上,不同的点有着不同的颜色信息等属性,于是就有了 纹理映射。
纹理(Texture)
任何一个三维物体,它的表面都是二维的,也就是说可以将三维物体表面上的点映射到一个二维平面上,而纹理就是在这二维平面上的一张图。
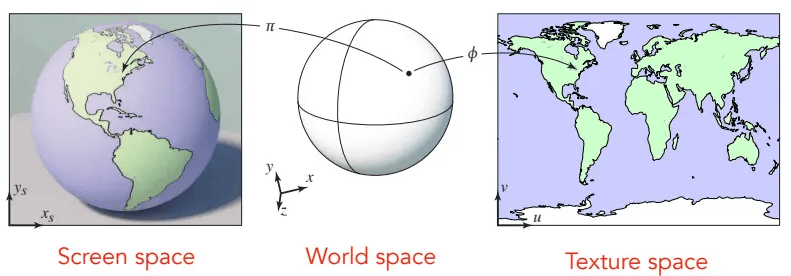
在渲染好的图片上,一个小方格管他叫像素;而为了区别,在纹理图片上,一个小方格管他叫纹素(Texel)。
纹理坐标(U-V)
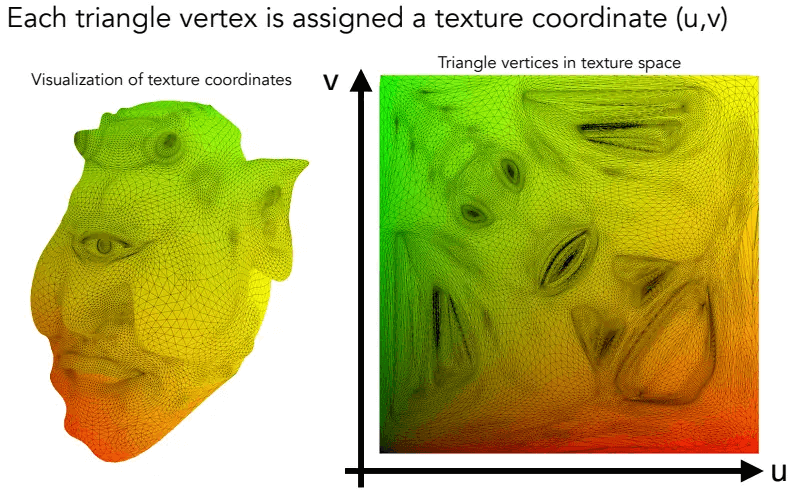
通过uv坐标,可以将3D中物体中每一个三角形顶点映射到材质上。在纹理坐标空间内,任意一个2D坐标都在
只知道三角形顶点坐标的uv,如何知道内部各个点的uv?又涉及到插值问题,详见前面的笔记。
可复用纹理(Tilable)
这种纹理的特征就是重复拼接后,上下左右都是连续的,可以贴到墙面和地板上。


伪代码
简易纹理映射的伪代码如下:

对每个光栅化的屏幕坐标算出它的uv坐标(利用三角形顶点重心坐标插值),再利用这个uv坐标去查询texture上的颜色,把这个颜色信息当作漫反射系数Kd。
纹理过小
纹理过小会导致严重的走样,因为屏幕空间上几个像素对应在纹理贴图上都是一个纹素,造成信息失真。
就近原则(Nearest)
什么也不考虑,像素离哪个纹素近,值就是那个纹素,会造成走样。
双线性插值(Bilinear Interpolation)
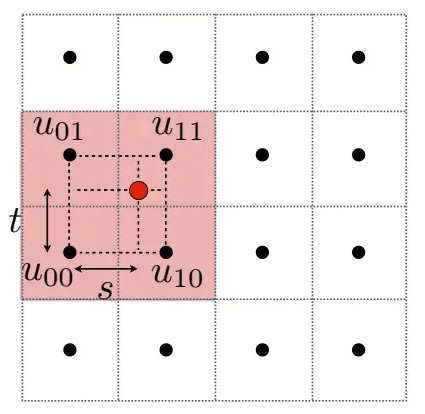
首先,如图所示,取红色像素旁边的四个纹素,算出该像素在水平和竖直方向偏移的比率s,t:
然后,利用1D线性插值和比例s,得到u01和u11之间的u1,u00和u10之间的u0:
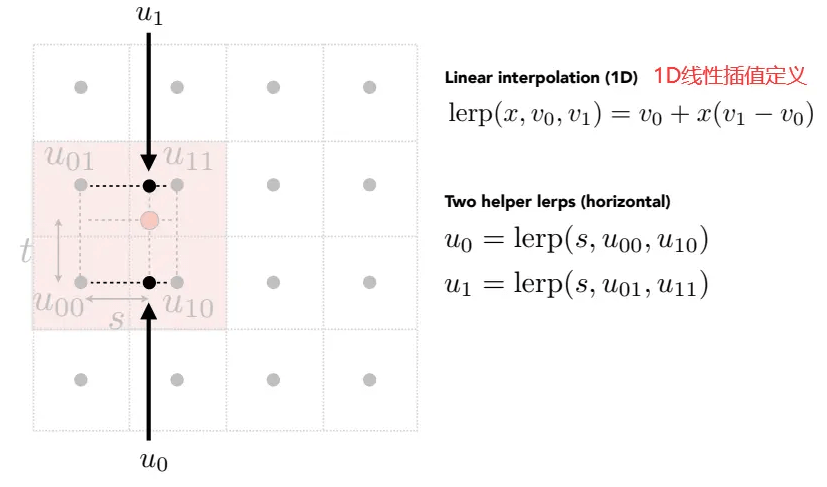
最后,再利用1D线性插值和比例t,得到该像素的值:
双三次插值(Bicubic)
利用三次方程进行两次插值,效果可能更好,但计算太麻烦了,且速度低。
三种方法的效果如图:

纹理过大
纹理不是越大越好,实际上,纹理过大,走样效果会更严重。从下图可见,本应出现左图效果,渲染后却出现了右图的各种走样:

形成走样的原因很明显,就是“近小远大”。如下图所示,我们在看近处的像素时,它所覆盖的纹素很小,看起来是连续的,不易走样;而看远处的像素时,它所覆盖的纹素很多,看起来是间断的,严重走样。这种现象被形象称为屏幕像素在纹理空间的Footprint。
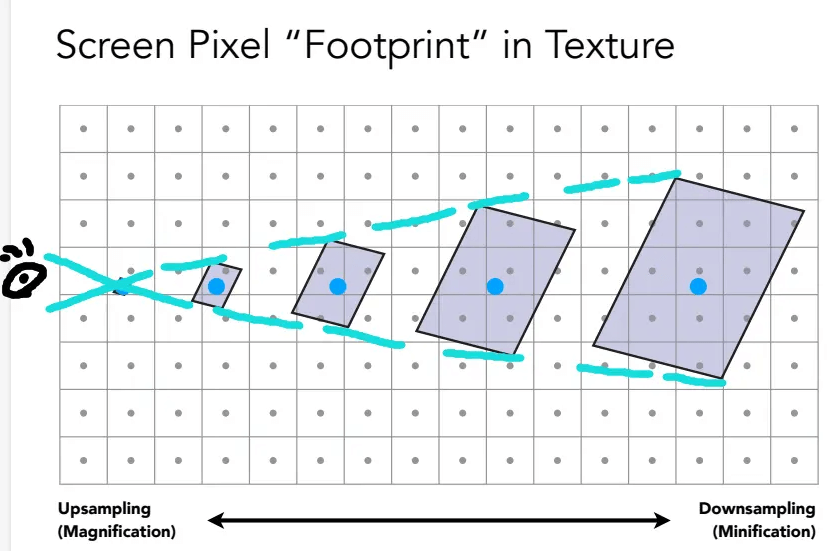
超采样(SS)
为了缓解以上问题,头一个直观的想法可能是超采样,把一个像素细分为很多小像素,这样他们覆盖的纹素就会变少。这样做的确能缓解走样现象,但不是最好的解法,因为计算量实在是太大了。

Mipmap
当然,也可以不采样,去求footprint区域里所有颜色信息的均值,这样就由点查询(Point Query)进阶到了区域查询(Range Query)。如下图,远处圈内的footprint肯定比近处的要大,因此需要准备不同级别(level)的区域查询。

基本概念
于是引入Mipmap,它允许进行 快的,近似的,正方形的 的范围查询:

随着level的提升,每升一级就把4个相邻纹素点求均值,合并成1个纹素,因此level越高,其查询的footprint区域更大。并且,使用mipmap,纹理图存储量只多了原来的三分之一。
计算Level D
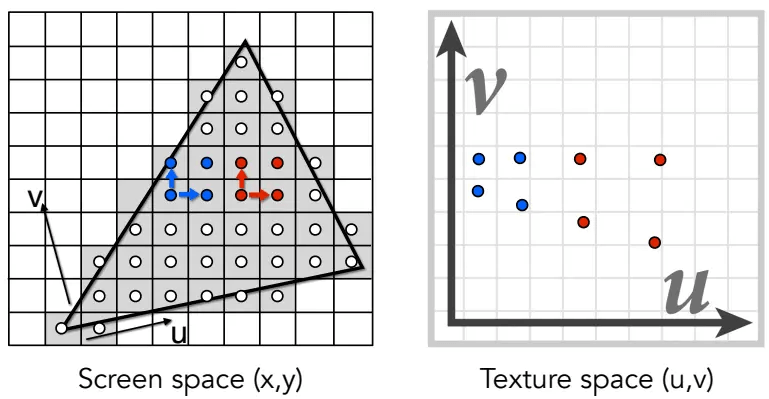
只需利用屏幕像素的相邻像素点去估算footprint大小,然后确定使用哪个level即可。
首先,在屏幕空间中找到四个相邻的像素点,将它们映射到纹理空间中:
然后,在纹理空间中,计算当前像素点离右边和上边像素点的距离,取最大值
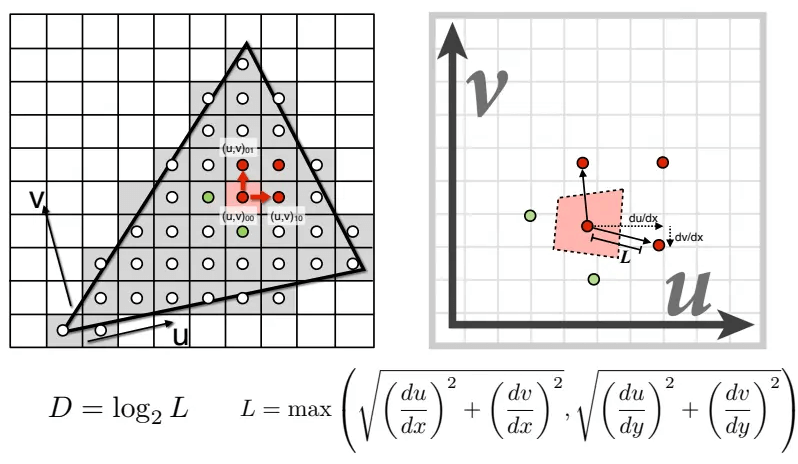
这样,就找到了近似 正方形footprint的大小和level D:
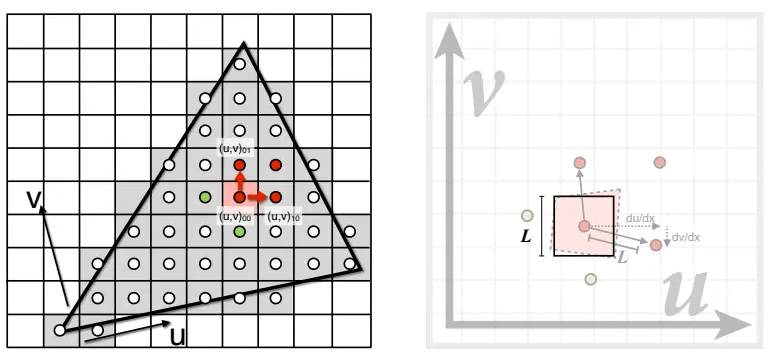
然而,这样子算下的D很大可能是一个小数,而不是整数,不明确。因此,有两种方法可以缓解此问题:
四舍五入取得最近的D:
![]()
这样子还是有些突兀,没有平滑过渡。
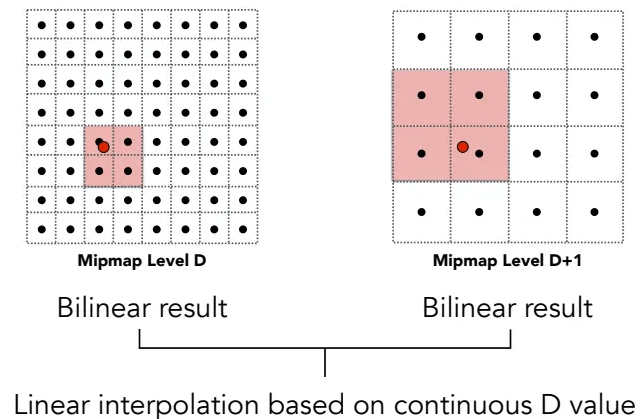
三线性插值(Trilinear Interpolation):
先在向下取整的D level进行一次双线性插值,再在D+1 level进行一次双线性插值,
最后,在这两次插值之间,进行一次线性插值,得到结果。
![]()
最后得到的结果也是平滑连续的,且本身开销很小(两次查询,一次插值)
![]()
各项异性过滤(Anisotropic Filtering)
用Mipmap渲染刚刚的纹理图,效果如下,发现远处太糊了:

产生这个现象的原因是,上面的mipmap都是用近似正方形的区域查询,而真实情况往往不是这么完美,一个像素所覆盖的纹理区域可能是不规则的:
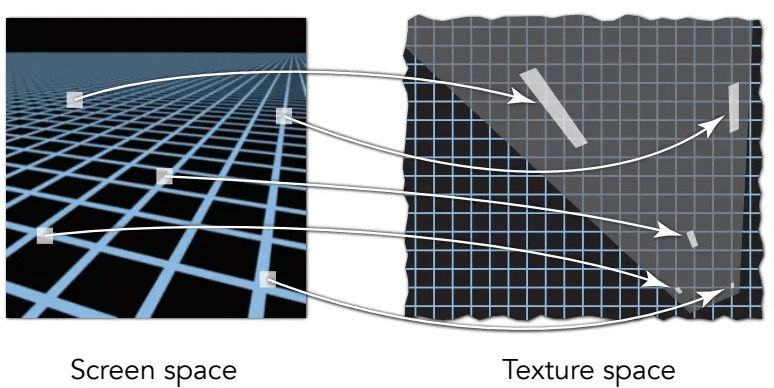
因此要引入各向异性过滤,即在不同方向上的表现各不相同,主要有两种方法:
Ripmap
允许对类似长条区域进行范围查询,但是不能用于斜着的区域。

EWA 过滤
把任意不规则的形状拆成很多不同的圆形,去覆盖这个形状,多次查询自然可以覆盖,但是耗时大。

应用
在现代GPU中,纹理就是一块内存+滤波/范围查询处理。因此,纹理可以存储许多东西,例如高度,环境光等。
环境贴图(Environment Map)
将环境光存储在一个贴图上,各个方向的光源可以用一个球体来存储:

也能像地球仪那样,把球表面展开,发现在极点处有扭曲问题:

可以用 立方体贴图(Cube Map) 来存储,在每个正方形面上存储环境光:

凹凸贴图(Bump Map)
也能将物体表面某点,逻辑上的“相对高度”存储到贴图中,表现出这个物体凹凸不平的样子:

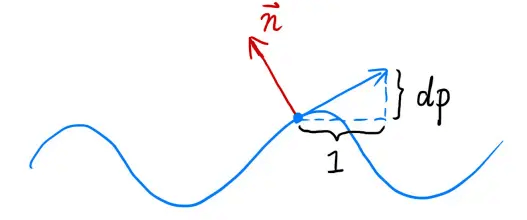
通过凹凸贴图,可以将原来平面的法线 p “扰动”为新的法线n:

那么如何计算法线n呢?
在平面上(flatland case),求某点p的新法线n:
- 原本在p点的法线
n(p) = (0, 1) - 在该点求导,即求该点在曲线上的切线,
dp = c * [h(p+1) - h(p)],其中,c是一个用于影响凹凸程度大小的常数,h(x)是x点的逻辑高度。 - 将该切线逆时针旋转90°即可得到新的法线:
n(p) = (-dp, 1).normalized().
在3D,求某点p的新法线n:
- 原本在p点的法线
n(p) = (0, 0, 1) - 在该点处求偏导,
dp/du = c1 * [h(u+1) - h(u)],dp/dv = c2 * [h(v+1) - h(v)] - 逆时针旋转90°:
n = (-dp/du, -dp/dv, 1).normalized()
然而实际情况上法线方向不是唯一的,这时候就要定义一个坐标空间,让法线方向唯一,然后通过一些变换转换到世界空间去。(待补充: 切线空间和TBN变换)。
位移贴图(displacement map)
凹凸贴图只是逻辑上描述了物体的凹凸,但位移贴图从 实际上 改变了物体的凹凸。它和凹凸贴图使用同样的纹理,但会改变三角形的顶点。

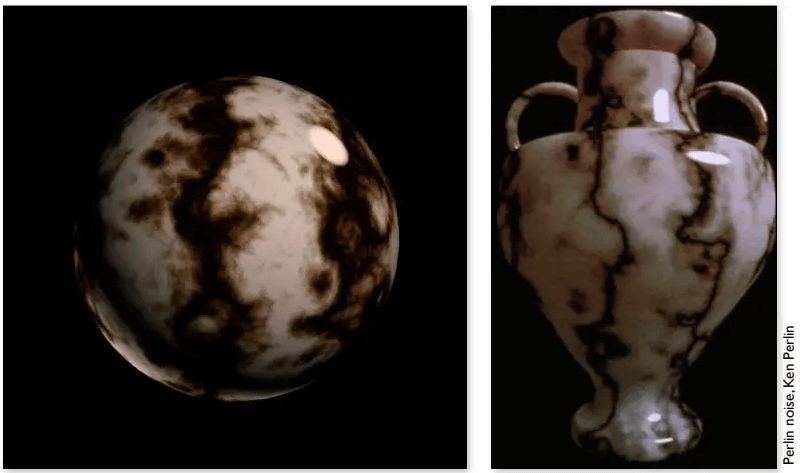
三维纹理
三维纹理,定义空间中任意一点的纹理。并没有真正生成纹理的图,而是定义一个三维空间的噪声函数经过各种处理,变成需要的样子。
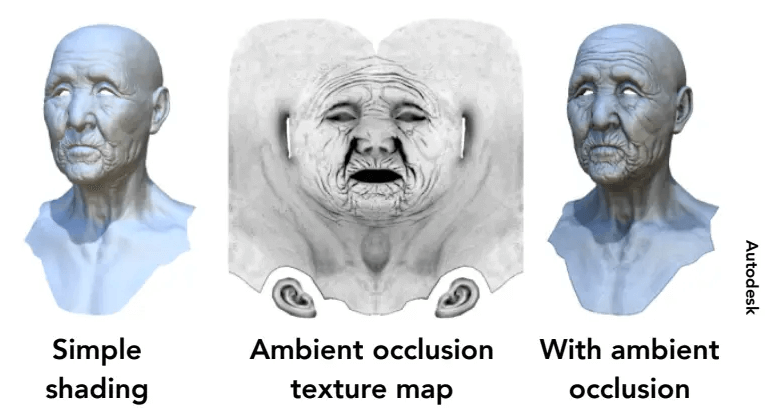
预计算阴影
阴影可以提前计算好,存储到纹理中。
阴影贴图(Shadow Mapping)
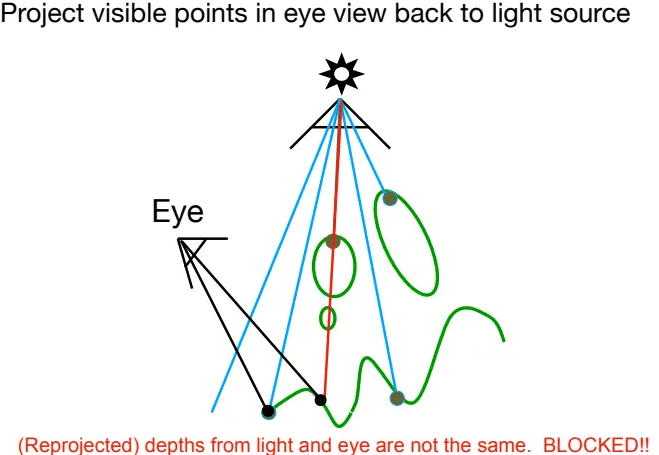
核心思想:不在阴影中的点必须同时被光和摄像机看见。因此,阴影贴图就得死摄像机能看见,光却照不到的地方。
经典的Shadow Mapping只能处理点光源,步骤如下:
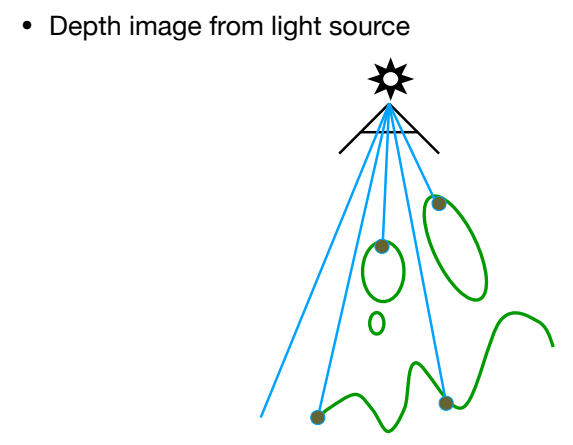
从光源开始渲染(看向这个场景):
![]()
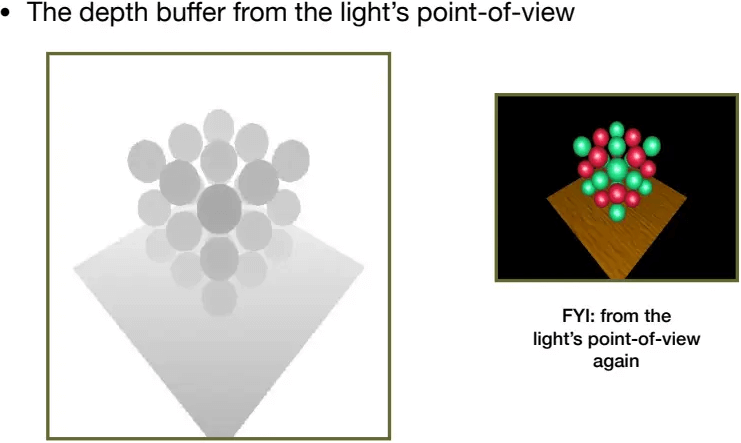
把光源当作摄像机,记录整个场景的深度Buffer,记作
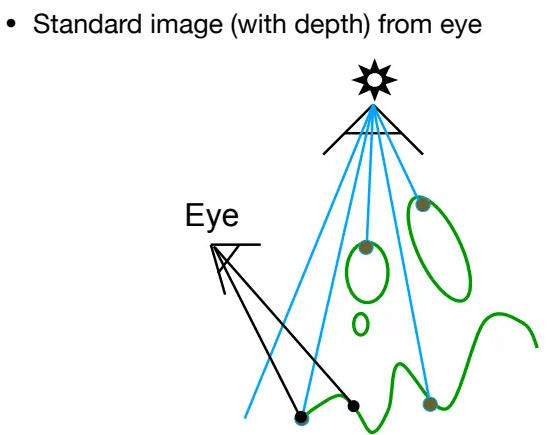
shadow maps从摄像机角度渲染一边场景,得到深度值:
![]()
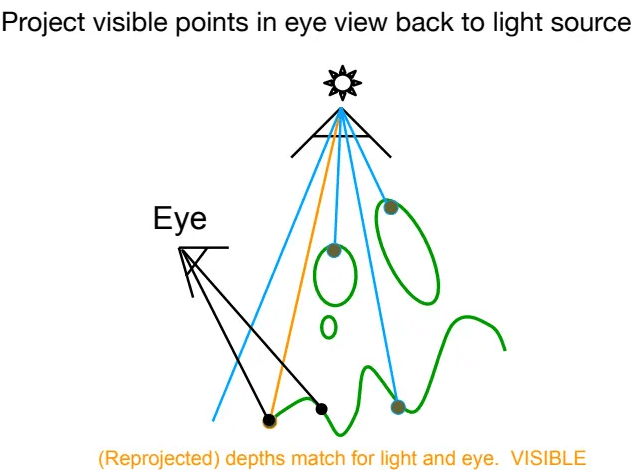
将摄像机视角的所有可见点坐标,通过光源视角的投影矩阵转换为其下的点坐标,然后可以找到对应
如果这个深度值与投影回光源的点的实际深度值相等,说明该点能被光源照射:
![]()
如果这个深度值小于实际深度值,则说明此点不可被光源看见,即该点前方有物体遮挡,在阴影中:
![]()
在阴影中的点,就不计算Blinn-Phong模型中的镜面反射/高光项和漫反射项了。
用实例演示如下:
首先,从光源开始渲染,记录下
shadow map:![]()
然后从摄像机开始渲染,并进行深度值的比较:
![]()
最终就得到上边的成果了。
Shadow Mapping的一些小问题:
浮点数难以判断相等,所以会留一个tolerance(小判断区间)
查询时不采用双线性插值,只寻找最近的点,因为倘若插值发生在物体边缘时,与邻接点的深度差距很大,会导致插值结果会有很大的误差
本身的分辨率会影响整体渲染质量
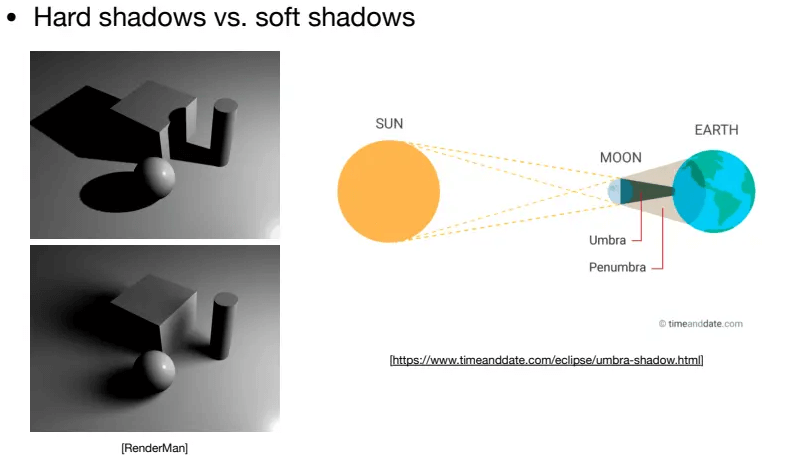
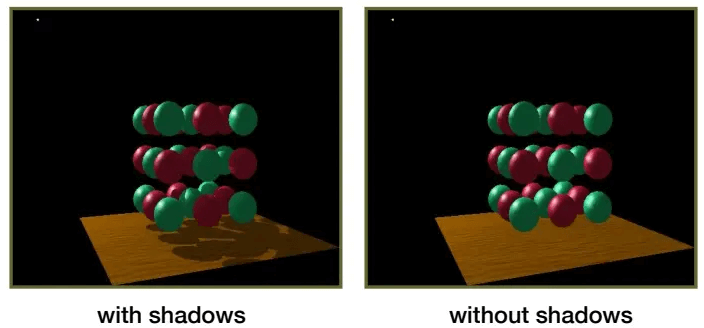
属于硬阴影,只适用于点光源。下图中,上边是硬阴影,下边是软阴影:
![]()
产生这种现象的原因是:光源也是有自己体积的。
参考资料
GAMES101-现代计算机图形学入门
计算机图形学七:纹理映射(Texture Mapping)及Mipmap技术 - 知乎 (zhihu.com)