着色

定义

给对象应用某种材质的过程。

着色点(shading point)

对于着色点，规定以下内容：

• 着色点所在的面是个平面（很小）
• 观测方向为
• 平面法线(Surface normal)为
• 光照方向
• 物体表面参数(颜色，材质反光程度shininess等等)

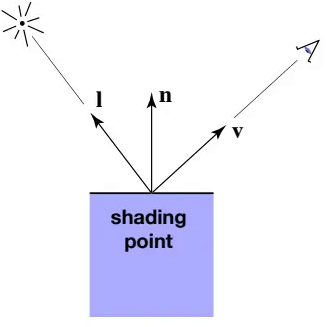
着色点是局部的，只考虑自己，不考虑其他物体的存在（不考虑阴影，shading和shadow是两回事）。

基本着色模型/局部光照模型

我们看到物体，实际上是人眼睛接收到了来自物体的光。

从上到下依次是高光(镜面反射)，漫反射（直接）和环境光照（间接，通过别的物体接收光），实际上，还有在杯子右边的发光源。

环境光照(Ambient)

环境光照即泛光反射，只考虑来自环境的光，为了简化计算，做一个大胆假设：

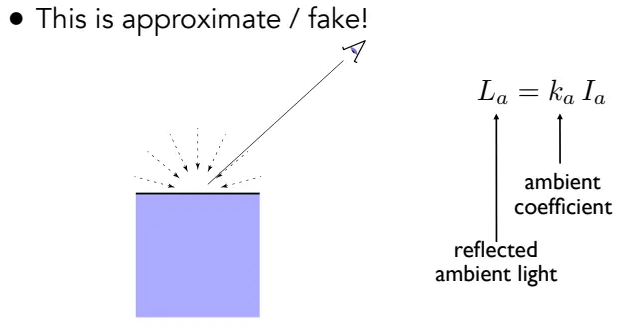
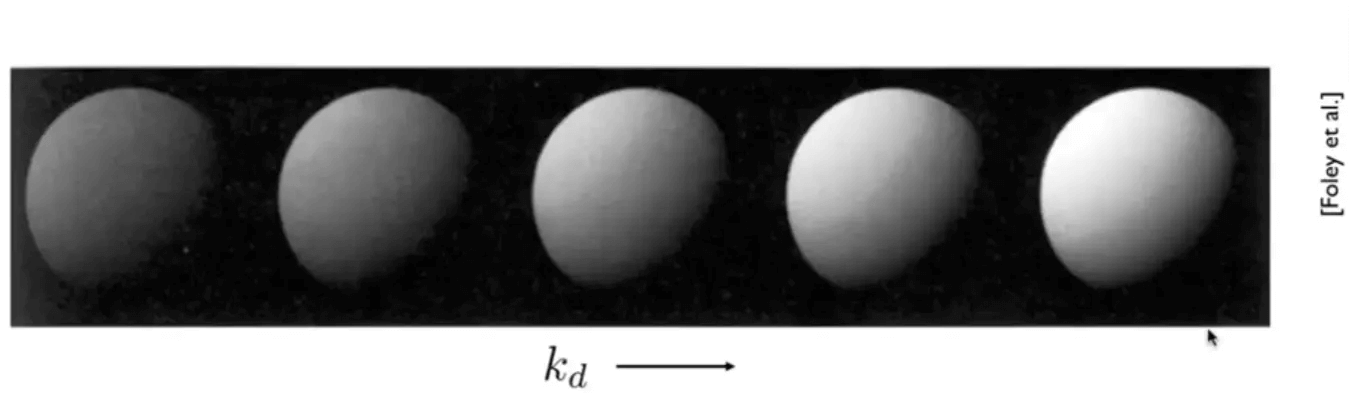
漫反射(Diffuse)

漫反射是光从一定角度入射之后从入射点向四面八方反射，且每个不同方向反射的光的强度相等，而产生漫反射的原因是物体表面的粗糙，导致了这种物理现象的发生。

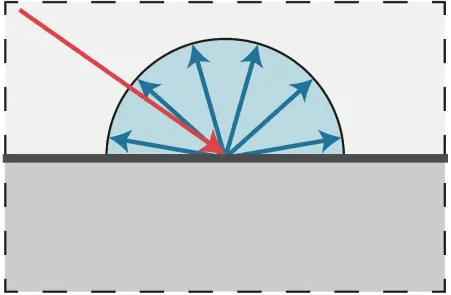
Lambert余弦定律

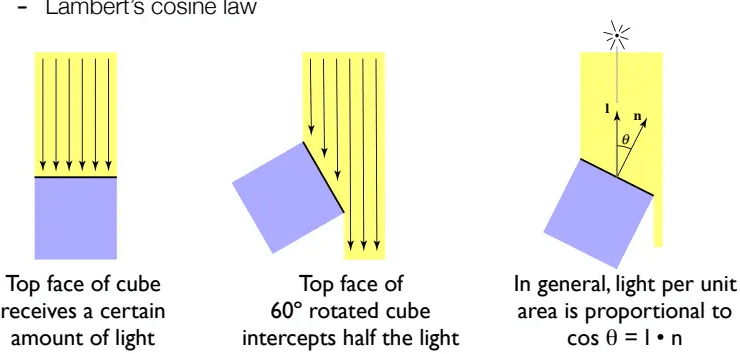
当入射光线与平面垂直的时候才能完整的接受所有光的能量，而入射角度越倾斜损失的能量越大，即光照方向与平面法线的夹角成比例： 最后的光强就是原来的光强乘上上边的。

能量衰减定律

光源与着色点间的距离也该考虑，离得越远光强越弱。

例如有个点光源，它发出的能量是一定的，在近处的球壳和在远处的球壳的总能量是相同的，但由于球壳表面积不同，离得越远其上某点获取的能量也就越小。

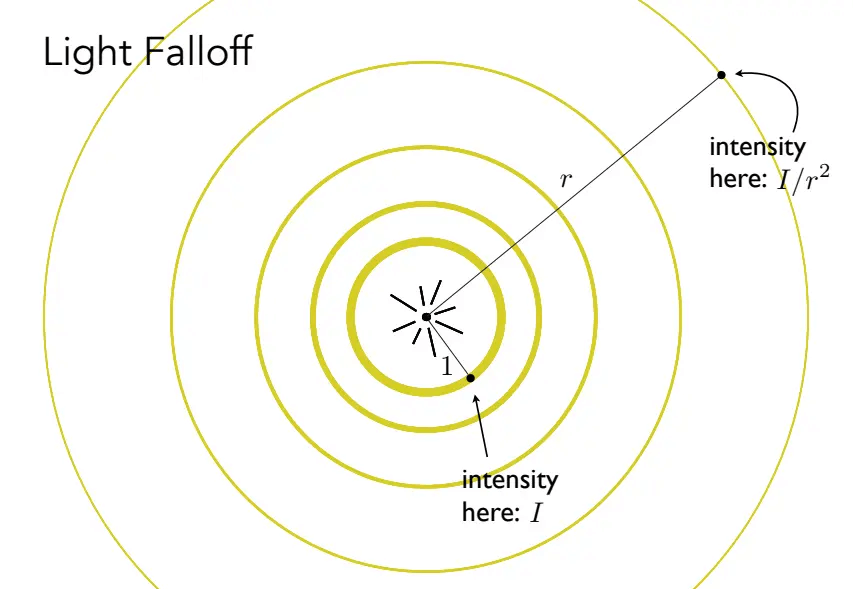
定义离光源距离为1的点，接收到光强为，那么距离为的点接收到的光强就是（由球的表面积 + 能量守恒求得）。

根据以上两个定律，就能模拟漫反射了：

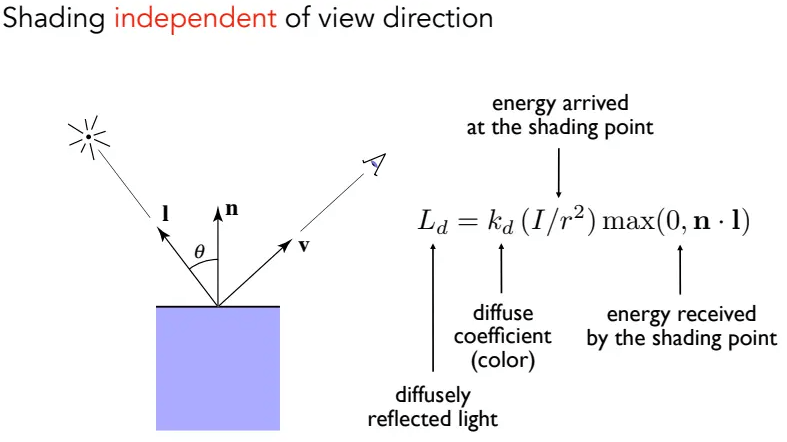
我们通过漫反射看到的能量由三部分组成：材质的漫反射系数，根据能量衰减定律得到的光强，根据Lambert余弦定律得到的光强。第三部分取max是因为角度超过直角后，就没有物理意义了。

镜面反射/高光(Specular)

Phong反射模型

其实就是一般的镜面反射：

是镜面反射方向，为人眼观察方向。高光只有在观察方向和反射方向比较接近的时候出现，其他情况只能看见漫反射等光，因此镜面反射会考虑他俩的夹角： 其中，是镜面反射系数，为入射光强，为入射光到着色点距离。指数p的意义在于加速衰减，因为离高光角度越远就越应该看不到，通常是100~200。

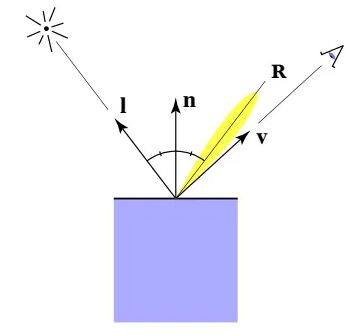
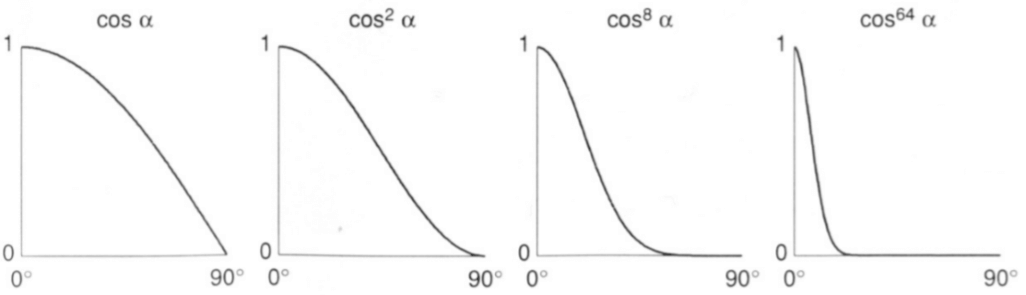
Blinn-Phong反射模型

为了提高运算效率，将反射方向与观察方向的夹角认定为半程向量和法线方向的夹角：

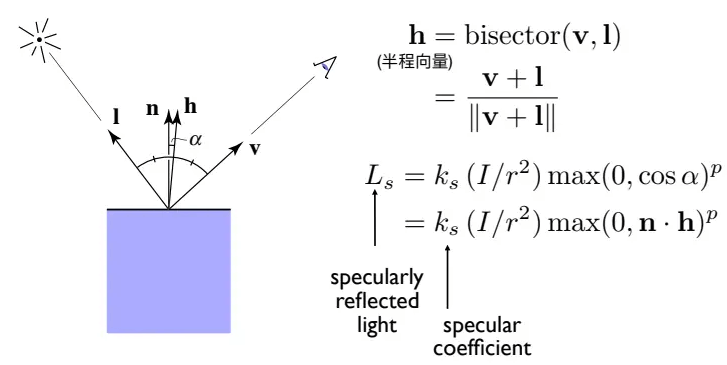
半程向量的计算很巧妙，只需将入射方向和观察方向的单位向量一加（角平分线），然后求单位向量就行。

这样，就得到了基本着色模型：

参考资料

• GAMES101-现代计算机图形学入门
• 计算机图形学五：局部光照模型(Blinn-Phong 反射模型)与着色方法