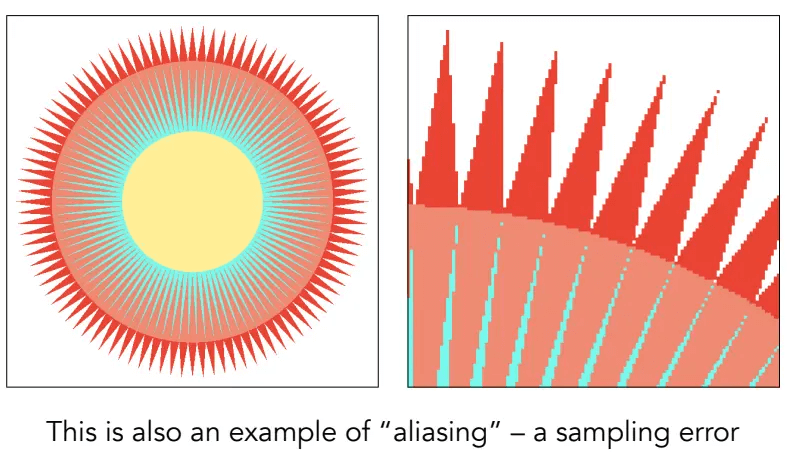
走样(aliasing)

采样角度

可以采样位置，得到照片；也能采样时间，得到视频；等等。

采样的瑕疵(Artifacts)

采样有多种瑕疵：

• 锯齿

• 摩尔纹

• 车轮效应

  (人眼在时间上的采样跟不上“车轮”运行的速度)

• …

造成走样问题的本质就是 信号变化的频率太快，采样速度跟不上。

频率角度

频域(Frequency Domain)

横轴是频率，纵轴是信号强度，用于描述信号在频率方面的特性。

傅里叶级数&傅里叶变换

傅里叶级数：任何周期函数都可以用正弦函数和余弦函数构成的无穷级数来表示。

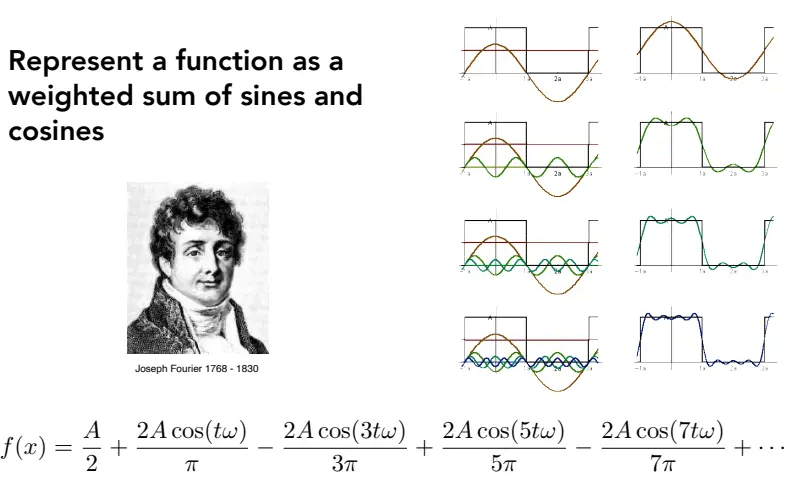
傅里叶变换：把给定信号分解为各个频率，即从时域（Spatial Domain）转换到频域（Frequency Domain）。

逆傅里叶变换：即傅里叶变换的逆过程。

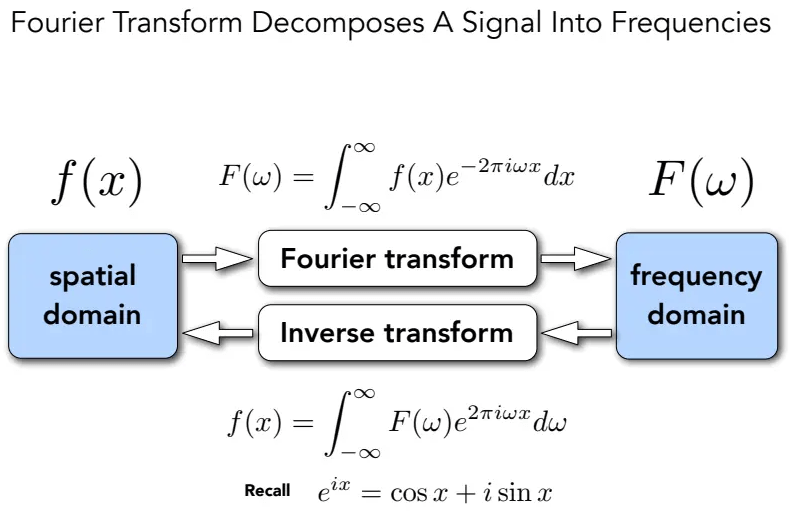
例如，将图片（时域）通过傅里叶变换转换为频谱图（频域）：

频谱图该怎么看，中间是低频区，越往外发散越高频。再看颜色，越亮，在此频率的信息越多。

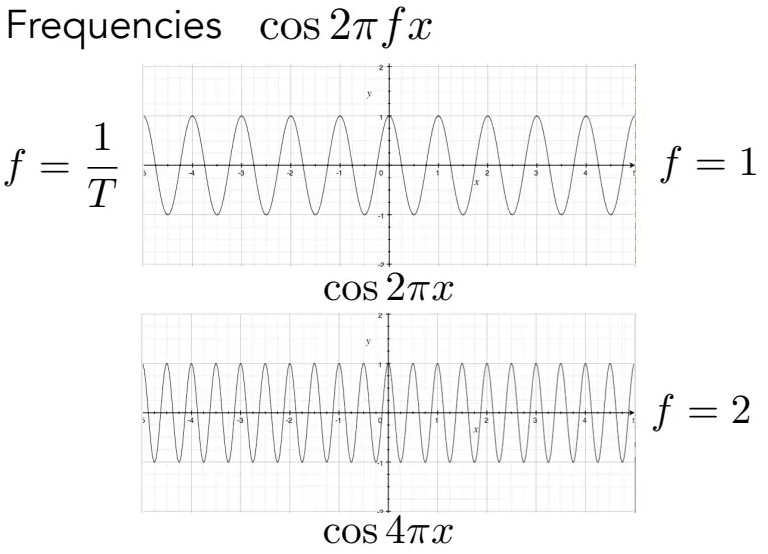
频率与走样

当频率低的时候，还能从采样点的连线推敲出原来的曲线大致是什么，但当频率高的时候，就推不出来了：

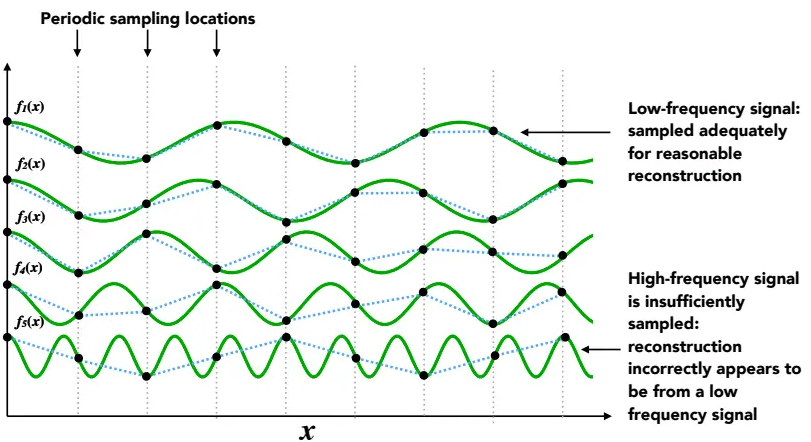
因此，频率高的信号还需要更快的采样，否则会造成走样。

并且，这样做还导致高频率信号和低频率信号在经过同样的采样后出现无法识别的情况，这也是走样的定义（频率方面）：

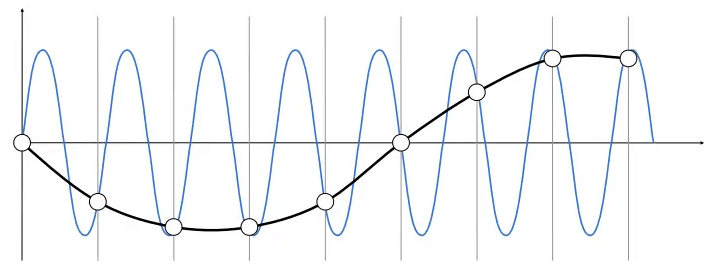
滤波(Filtering)

一种特殊的信号，可以将某些频率给去除掉。

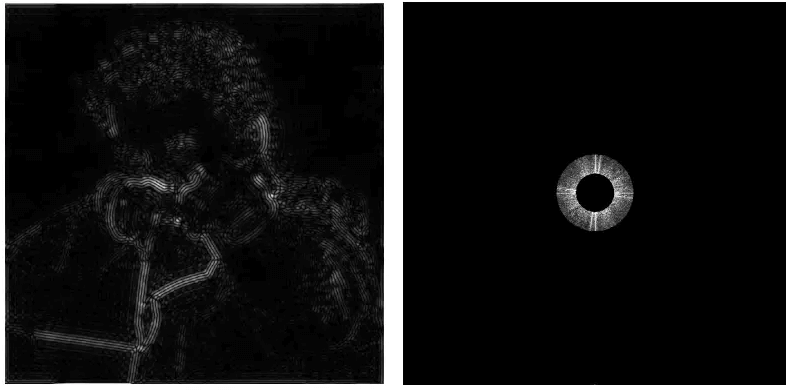
高通滤波

只让高频信息通过，它可以保留图片内容的边界（周围发生剧烈颜色变化的地方，例如本图的白纸和黑衣服）。

低通滤波

只让低频信息通过，让图片模糊（因为看不到边界）。

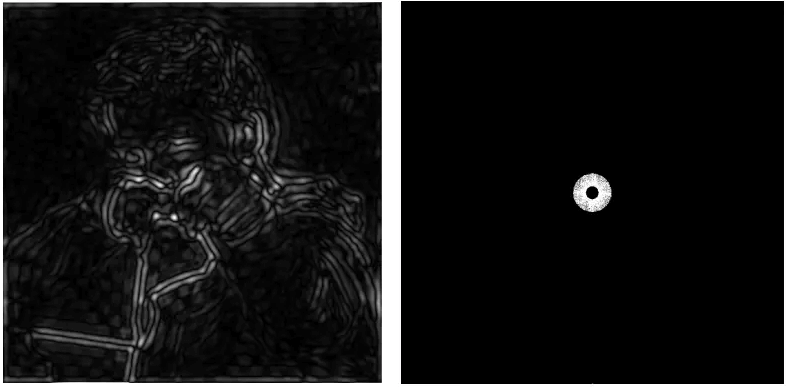
带通滤波

只允许某一段频率的信息通过，得到不那么明显的边界特征。

卷积(Convolution)

（图形学角度）

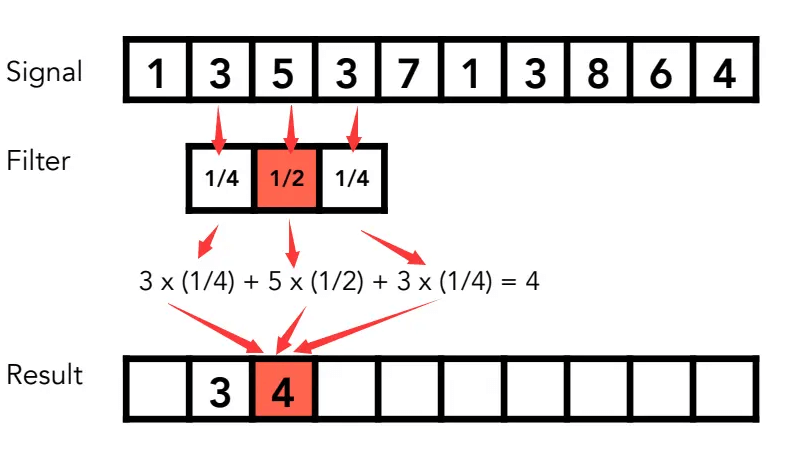
在原始信号的任何位置，用一种滤波操作，取他和他周围的平均数，此过程就是卷积，最终会得到一个结果。

卷积定理

在时域上的卷积 = 在频域上的乘积；在时域上的乘积 = 在频域上的卷积除以2π

因此，做卷积操作就有了两种选择：

1. 直接通过滤波器（也称卷积核）在时域上进行卷积。下例中，是通过取某像素和它旁边像素的平均值完成的。
2. 先把时域通过傅里叶变换为频域，然后将频域与滤波器相乘，最后把结果通过逆傅里叶变换为时域。

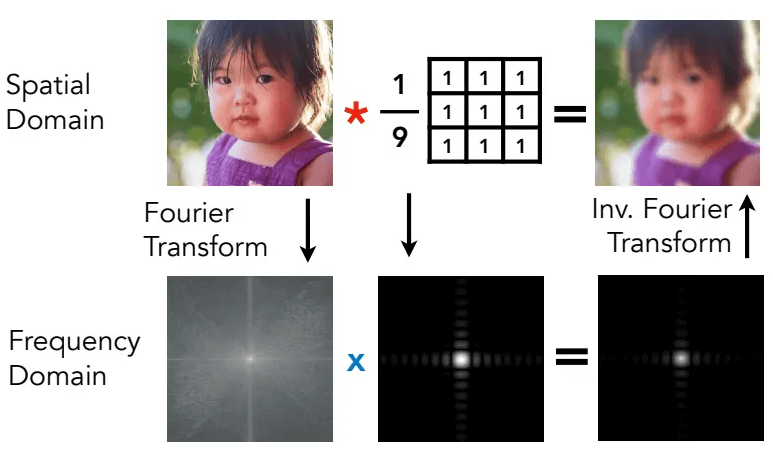
卷积核/滤波盒

对于3x3的卷积核，如果不乘1/9，会导致卷积后的像素很大（因为一个像素里有九个像素的和），使得图片很亮（接近于白色）。

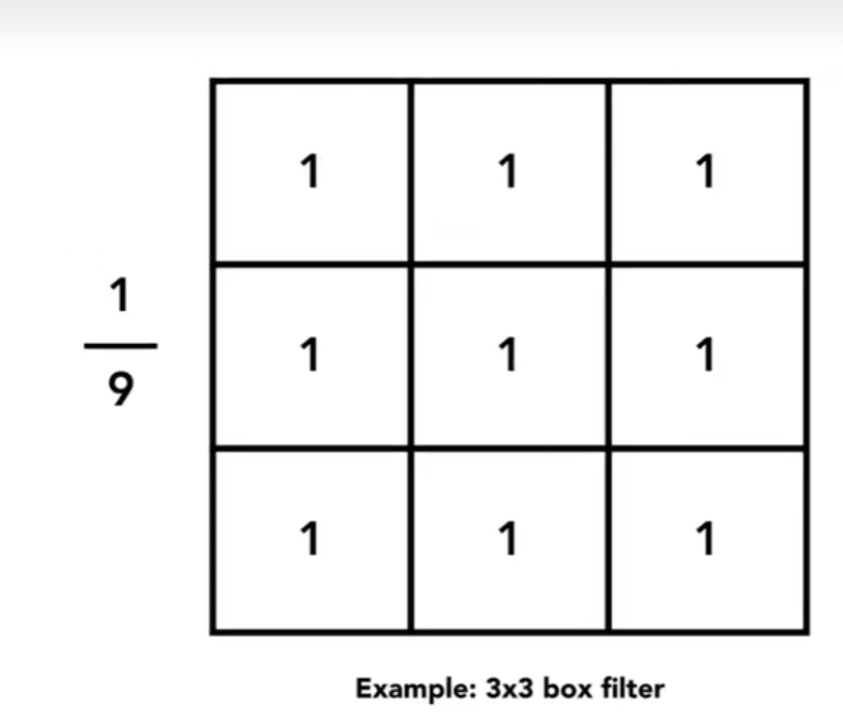
在频域角度（卷积核经过傅里叶变换），可以发现，时域越大，参与模糊的信息越多，频率越小。

频率与采样

实际上，采样就是在重复频率上的内容。

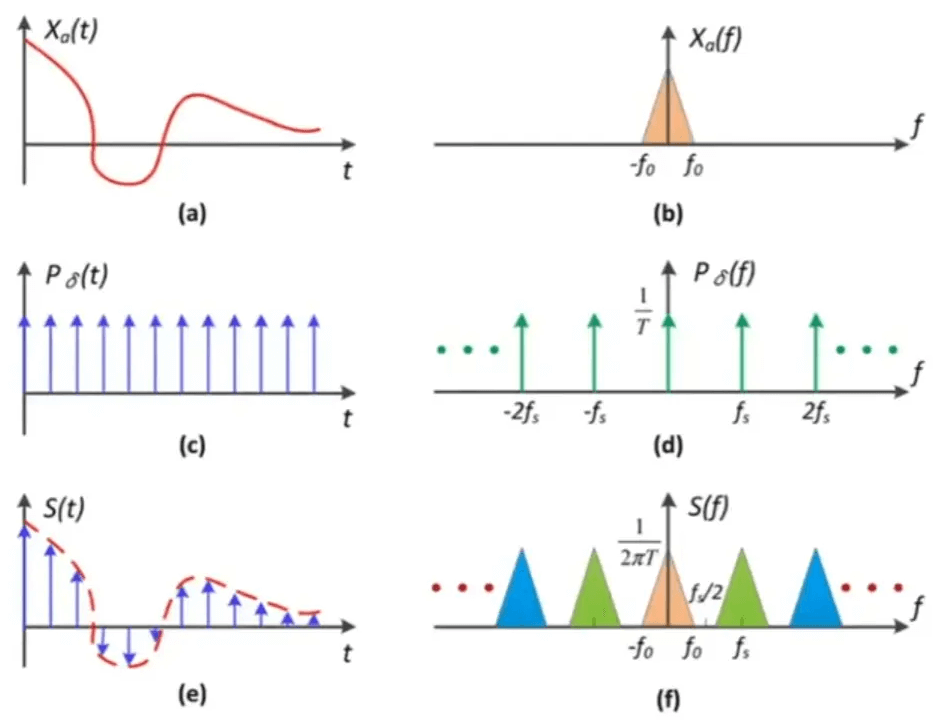
在时域上（左边），连续函数(a)和冲激函数(c)相乘，得到采样结果(e)；在频域上（右边），根据卷积定理，时域的乘积就是频域上的卷积除以2π，得到卷积结果(f)。

从(f)理解走样，就是由于采样不够快，导致频率有了重叠，发生走样。

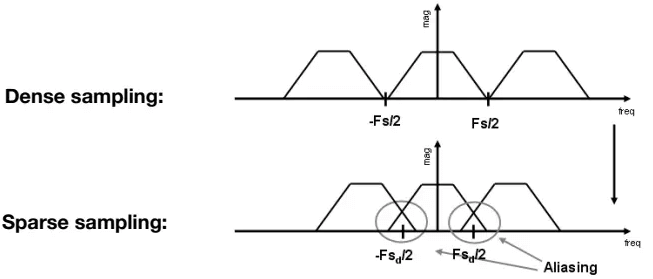
反走样(antialiasing)

原理

可以增加采样率，这是在设备上解决的，而不算是真正的反走样。

也可以在采样前进行预处理（模糊、滤波等），然后采样，可以减少瑕疵。

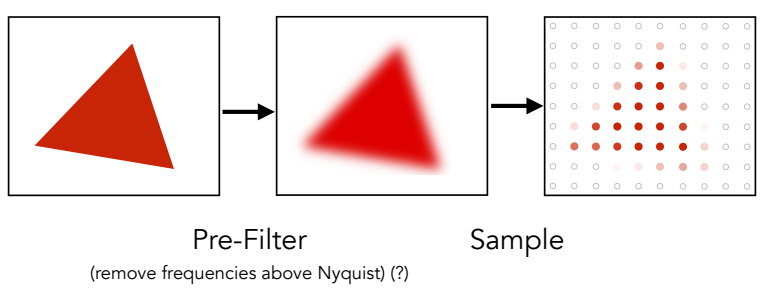
一定要注意顺序，如果先采样后反走样，效果就会不好。

预处理的详细意思就是先把信号的高频信息拿掉，然后再采样，这样可以缩窄频率宽度，减小混叠，从而避免走样。

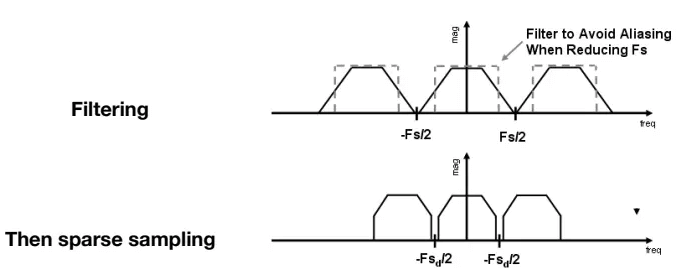
主要步骤

选择卷积核/滤波盒

要想对三角形进行模糊处理，选择合适的卷积核很重要。1个像素宽的低通滤波器即可：

进行反走样

选好卷积核，就能进行反走样操作了：

• 用选好的卷积核对f(x, y)的每一个像素进行卷积操作
• 对每个像素中心点进行采样操作

而f(x, y)在三角形这个问题中就是inside(tri, x, y)：

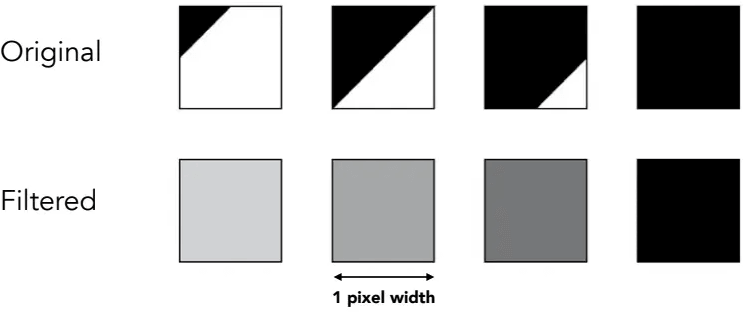
黑色部分为三角形覆盖部分，经过卷积操作后，可以将原来三角形在本像素覆盖了多少转换为本像素对应的灰度。

具体方法

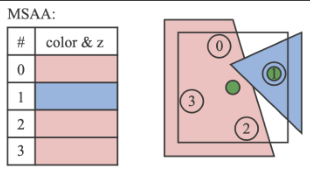
MSAA

多重采样（Multi Sampling Anti-Aliasing），单个像素也能被分为若干小像素，每个小像素也有自己的中心点：

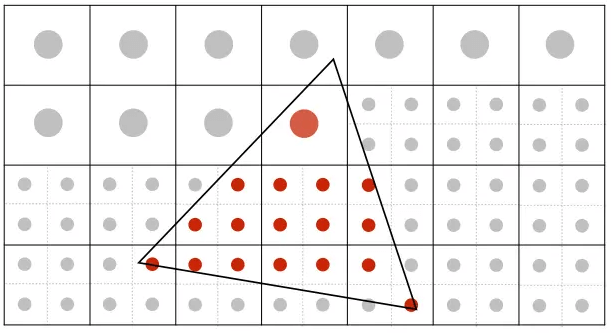
接下来计算大像素内小像素的覆盖率并反映到像素的rgb，即可得到“模糊”的结果（ps：第三行第三列也应该是75%）：

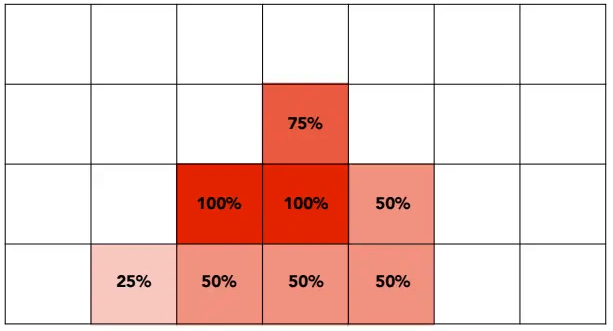
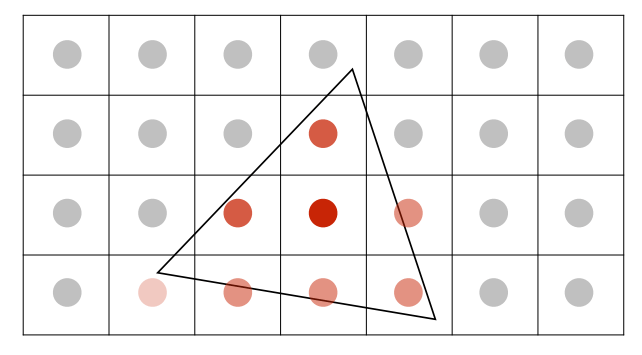
此外，MSAA还有一些性能优化：

• 相同的图元只被着色一次

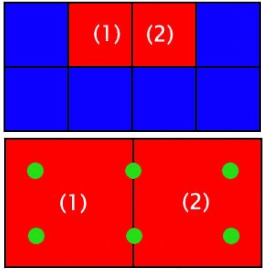
• 允许重用周围的采样

  例如在这两个像素中，像素1可用4个小像素，像素2可用4个小像素，中间的的两个小像素就是共用的。

SSAA

超级采样抗锯齿（Super Sampling AA），和MSAA相似，但分成小像素后，不是计算覆盖率，而是通过直接计算4个小像素的rgb平均值，从而间接“得到”原来像素的值。

一个简单的理解是，把场景按照几倍的分辨率先渲染，然后进行降采样操作，是最终解法，但性能消耗十分大（掉帧厉害）。

FXAA

快速近似抗锯齿（Fast Approximate AA），他和采样无关，先得到有锯齿的图，然后进行相关处理（把有锯齿的边界替换为无锯齿的边界），最终快速地获得到抗锯齿的图。

TAA

时域抗锯齿（Temporal AA），很快，和MSAA差不多，但计算的时候会考虑复用上一帧所感知的结果。

DLSS

深度学习超级采样（Deep Learning Super Sampling），基于超分辨率技术和深度学习，从低分辨率图片生成高分辨率图片，然后再缩回去，得到“抗锯齿”图像。

SMAA

即Enhanced Subpixel Morphological AA，是处理基于图像的抗锯齿的最好方法。基于FXAA得到MLAA（即Morphological AA），然后由MLAA加强得到SMAA。

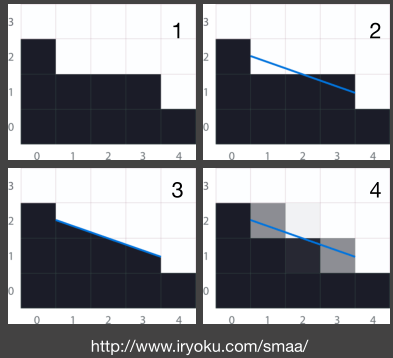
对于走样（1），先找到边界（2），然后得到理想效果（3），最后根据理想效果把对应像素填进去（4）。

参考资料

• GAMES101-现代计算机图形学入门
• Games101｜作业2 + 光栅化 + SSAA vs MSAA + 黑边问题 - 知乎 (zhihu.com)