三角形图元(Triangle Primitive)

三角形是最基础的多边形，且任何多边形都能拆解为三角形。除此之外，还有优点如下：

• 三角形内一定是平面
• 三角形内部外部定义清晰
• 定义三个顶点后，可以在三角形内做“渐变”（插值）。

经过MVP变换和视口变换，我们已经得到屏幕上三角形的顶点坐标了，接下来该怎么变成对应的像素三角形？

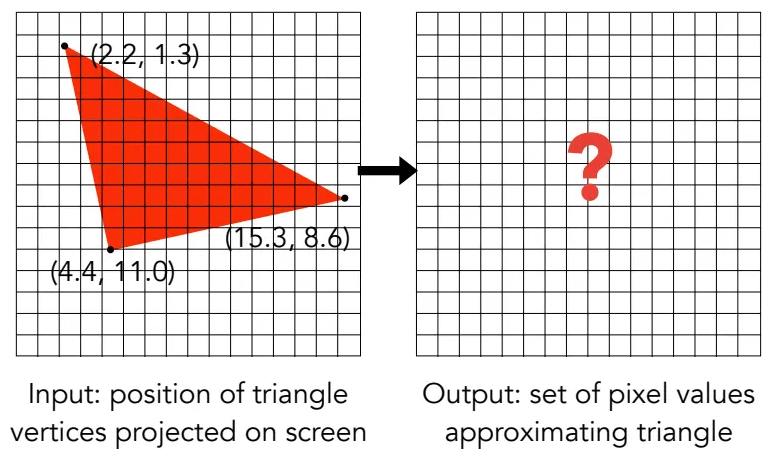
采样(Sampling)

把连续函数离散化的过程，就是采样。

for (int x = 0; x < xmax; ++x)
    output[x] = f(x);

在图形学中是很重要的概念，涉及到像素，时间，等等。

光栅化采样

光栅化采样的目的就是 判断像素中心是否在三角形内。

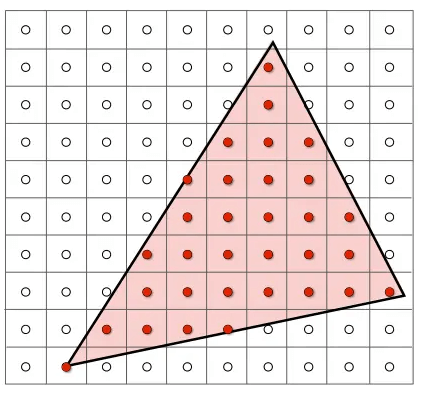
定义函数原型： 在2D中，可以这样写：

for (int x = 0; x < xmax; ++x)
    for (int y = 0; y < ymax; ++y)
        image[x][y] = inside(tri, x + 0.5, y + 0.5);

如何判断？使用向量叉乘。(通常)逆时针地，判断点是否在三条边的同侧，如果是的话就在三角形内。

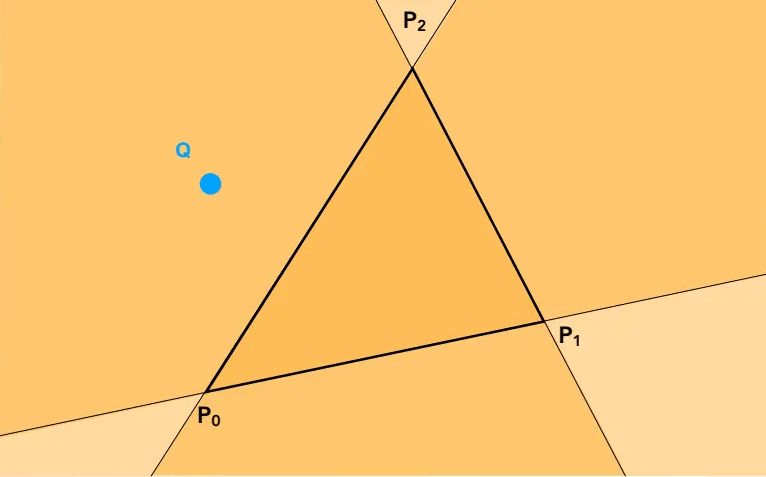
例如上图中，应判断，，是否同向。

PS：如果点在边界上该怎么办，可以不做处理(GAME101)，也能做特殊处理(OpenGL, DX)。

遍历像素点

包围盒(Bounding Box)优化

难道需要遍历整个屏幕上的像素点来完成采样吗，当然不需要，只需划定一小片区域即可，这就是包围盒(BB，也称轴向包围盒AABB)：

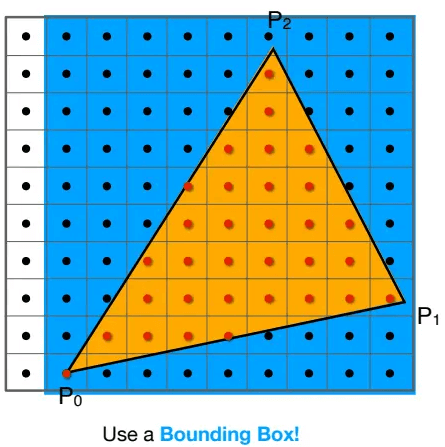
增量三角形遍历(Incremental Triangle Traversal)优化

有时候会碰到又窄又长的三角形，用AABB会浪费很多时间。可以使用此方法进行遍历，相当于给三角形每一行都确定一个AABB，但实现起来难度可能会大。

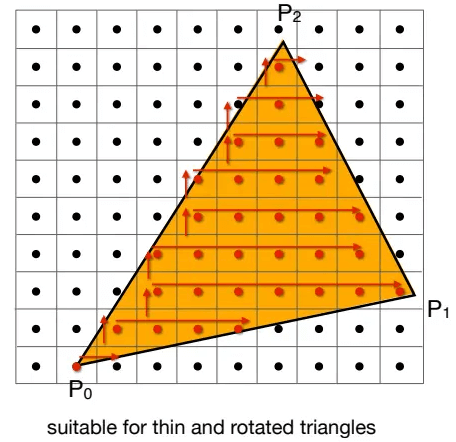
最终采样结果如下：

把他用像素显示出来，却是这个丑样子：

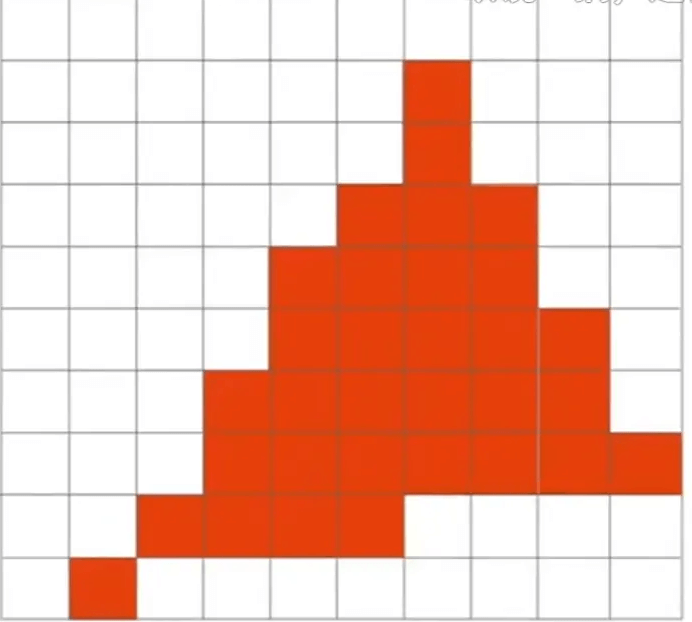
由于像素本身占一定的大小，且我们的采样率不够高，产生走样问题(Aliasing)，在图形学中体现为锯齿(Jaggies)。接下来就要抗锯齿/反走样。

参考资料

• GAMES101-现代计算机图形学入门