MVP变换

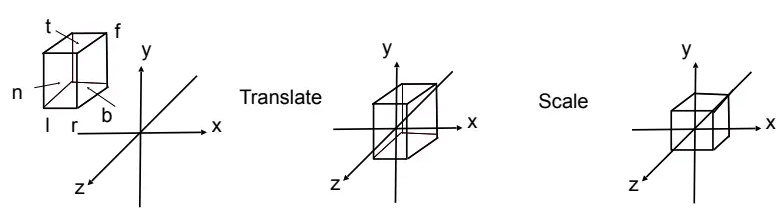
MVP变换就是将三维物体变换到二维中，就像拍照片一样：

1. 模型变换(Model Transformation)：模型空间 -> 世界空间，即摆好模型，搭好场景。
2. 视图变换(View Transformation)：世界空间 -> 相机空间，即给场景找到一个好的摄影角度。
3. 投影变换(Projection Transformation)：相机空间 -> 屏幕空间，即进行拍照，得到照片。

视图变换

首先，先定义相机（观测矩阵）：

• 相机的位置：
• 相机“看”的方向：
• 相机向上的方向：

如何进行视图变换？把相机和它所拍摄的场景”移动”到一个规定好的位置即可，这个位置(右手系 )通常为世界坐标的原点，向上为Y，看的方向为-Z：

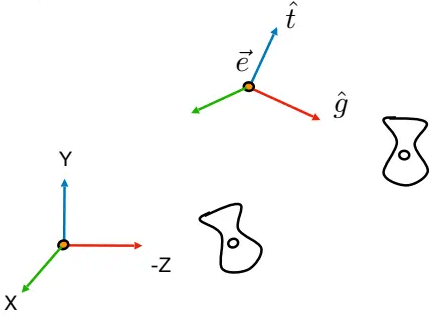
“移动”的过程如下：

1. 将相机移动到原点（一个简单的平移+引入齐次坐标）：

2. 通过旋转，将旋转到方向、将旋转到方向、将旋转到方向。

   但是仔细想想，把一个方向不规范的坐标空间旋转成方向规范的坐标空间，所需的旋转矩阵应该不好写。因此，可以考虑从规范坐标空间（世界空间）旋转到当前坐标空间（相机空间）的逆矩阵（引入齐次坐标）： 由于旋转矩阵是 正交的，那么它的逆矩阵就是它的转置矩阵。因此，最终得到的旋转矩阵为：

将平移操作和旋转操作组合（列向量从右往左），得到的最终矩阵如下：

投影变换

接下来进行投影变换，将相机框内的东西拍成一张照片。投影主要分为 正交投影和透视投影两种：

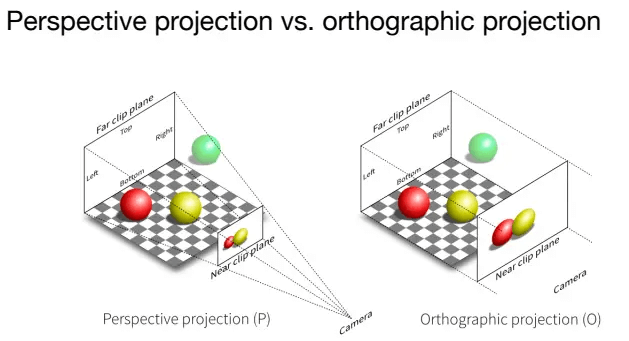
透视投影会带来“近大远小”的现象，而正交投影不会。

正交投影(Orthographic)

正交投影的正式做法如下：

1. 定义一个立方体，用它框住想要正交投影的所有物体。

2. 通过平移和缩放，将该立方体标准化为:

然后，上边变换用矩阵表示就是： Ps：由于左右手系有些地方不同，如果结果不正确，尝试给Z轴相关的运算取个相反数。

透视投影(Perspective)

运用得最广泛，满足“近大远小”性质。透视投影可以看出是特殊的正交投影，用“远平面”和“近平面”框住物体，先把“远平面”向“近平面”挤压，挤压成类似于正交投影的小盒子，然后做一次正交投影。

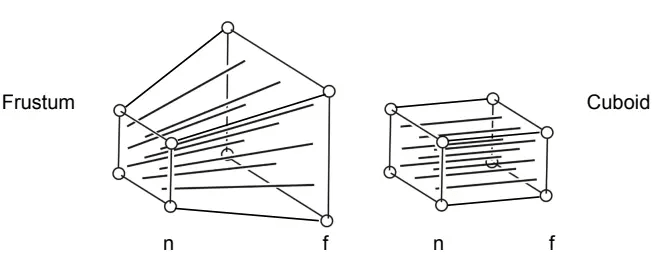
透视投影的做法如下：

1. 把“远平面(z)”向“近平面(n)”挤压。规定“近平面”永远不变；挤压时，“远平面”的z值不变，但他俩之间的要发生变化；“远平面”的中心点始终不变。

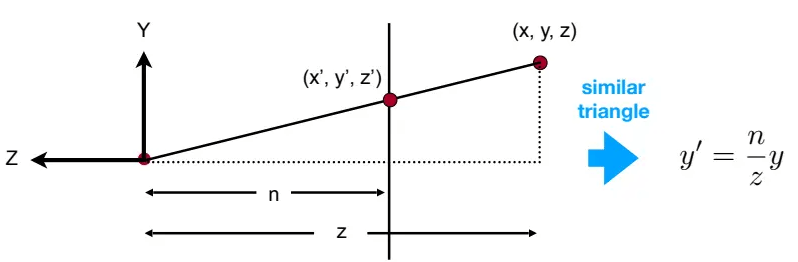
   在挤压过程中，x，y的比例关系（相似三角形）如下：

   引入齐次坐标的概念。假设挤压前，远平面某点为，经过挤压，它的坐标变为。根据齐次坐标的性质，该点还能被表示为（同乘z，z不为0）。

   现在，挤压前后的点坐标都知道了，剩下求转换矩阵： 求得：

   由于近平面不变，近平面上某点也不变（n是近平面位置），于是有： 所以缺失的一行应该是这样子的： 解得

   由于远平面的中心点是始终不变的（f是远平面位置），同理有： 两式联立，解得 得到挤压时的转换矩阵：

2. 进行正交投影。

最终得到的透视投影矩阵为：

如果观察的是Z轴的负方向（如OpenGL），那么投影矩阵是： 注意：

这里有问题，做完西交大图形学实验才知道这里的n，r，f啥的我搞混了，解释一下：左上角两个n对应上图的，是摄像机到参考点的距离；右下角的n和f是近平面和远平面距离坐标轴的距离。

一些概念

视锥体(View Frustum)

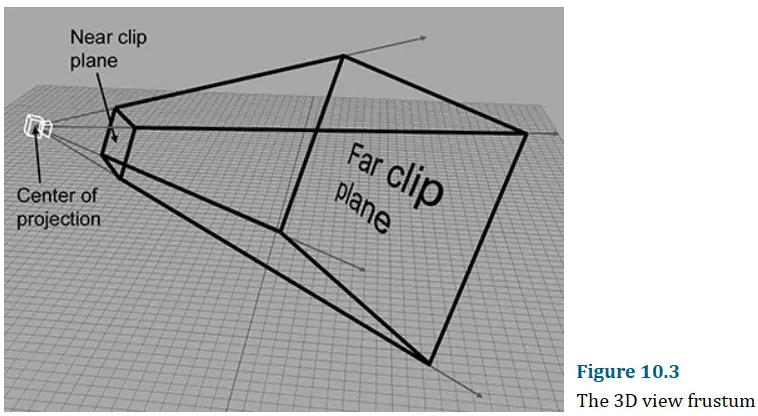
视锥体是相机可能看到的空间体积，它的形状像金字塔，只是尖端被剪掉了。

衍生的定义还有：

• 视野（Field Of View，FOV）：视锥体截取的角度，分水平和垂直两种。
• 宽高比（Aspect）：视锥体矩形截面的宽度与高度的比值。

一般来说，知道宽高比和垂直的fovY，就能定义一个视锥体了。

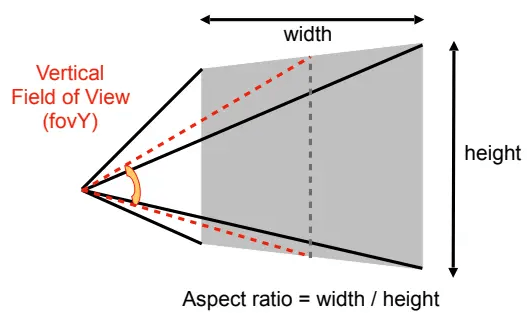
还能利用它俩推出视锥某矩形截面的l，r，b，t：

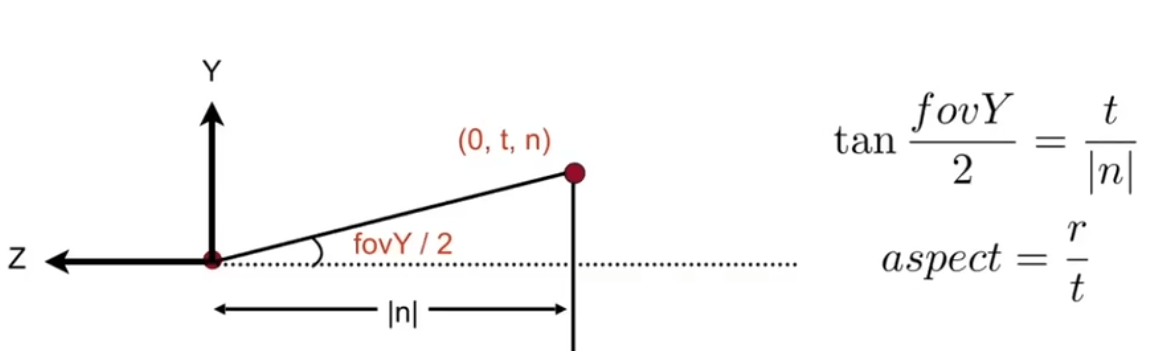
透视矩阵也能写成这样：

屏幕(Screen)

• 二维数组，元素为像素
• 数组的大小就是屏幕的分辨率了
• 一种典型的光栅(Raster)成像设备，光栅化(Rasterize)就是把成像内容画到屏幕上。

屏幕空间(Screen Space)

认为屏幕左下角是原点，向右是x，向上是y。

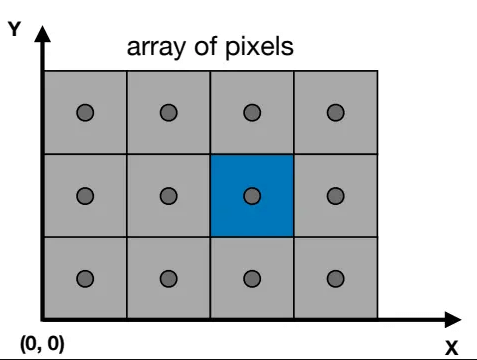
通常有以下规定：

• 像素的坐标是(x, y)形式，x，y都是整数。
• 像素坐标的范围是(0, 0)到(width-1, height-1)。
• 像素的中心位置是(x+0.5, y+0.5)。
• 整个屏幕覆盖(0,0)到(width, height)。

视口变换(Viewport)

将MVP变换后得到的“照片”映射到屏幕空间中。

先不管Z坐标，那么只需将内的内容变换到上就行：

参考资料

• GAMES101-现代计算机图形学入门
• 3D数学基础 图形和游戏开发(第2版)