齐次坐标(Homogeneous Coordinate)

给点和向量的描述升一维（），以2D为例：

• 二维中的点：
• 二维中的向量：

这里理解一下为什么点的，向量的。

在三维中处的标准二维平面，实际的二维点此时表示为。而对于那些不在平面的点，则可以通过除以，将它们投影到平面上。这样，齐次坐标就能够映射到实际的二维点：

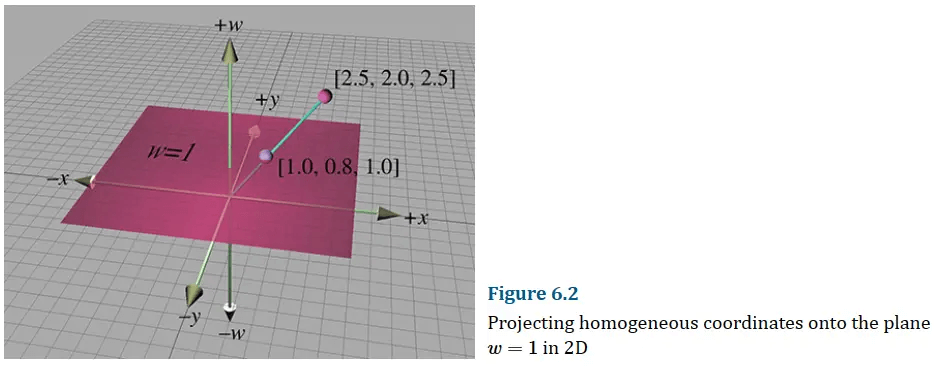
对于任何给定的二维点，在三维齐次空间中存在无限数量的对应点。这些点形成一条穿过三维齐次空间原点的直线。

当时，上面的除法未定义，而向量恰好没有在空间中平移的概念（都一样），因此可以用来描述向量。

并且根据w的特性，可以快速判别两个点/向量的关系：

• 向量+向量=向量 （0+0=0）
• 点-点=向量（1-1=0）
• 点+向量=点（1+0=1）
• 点+点=中点（1+1=2 表示点）

线性变换(Linear)

形如的变换，即。包括下面的缩放，反射，错切和旋转。

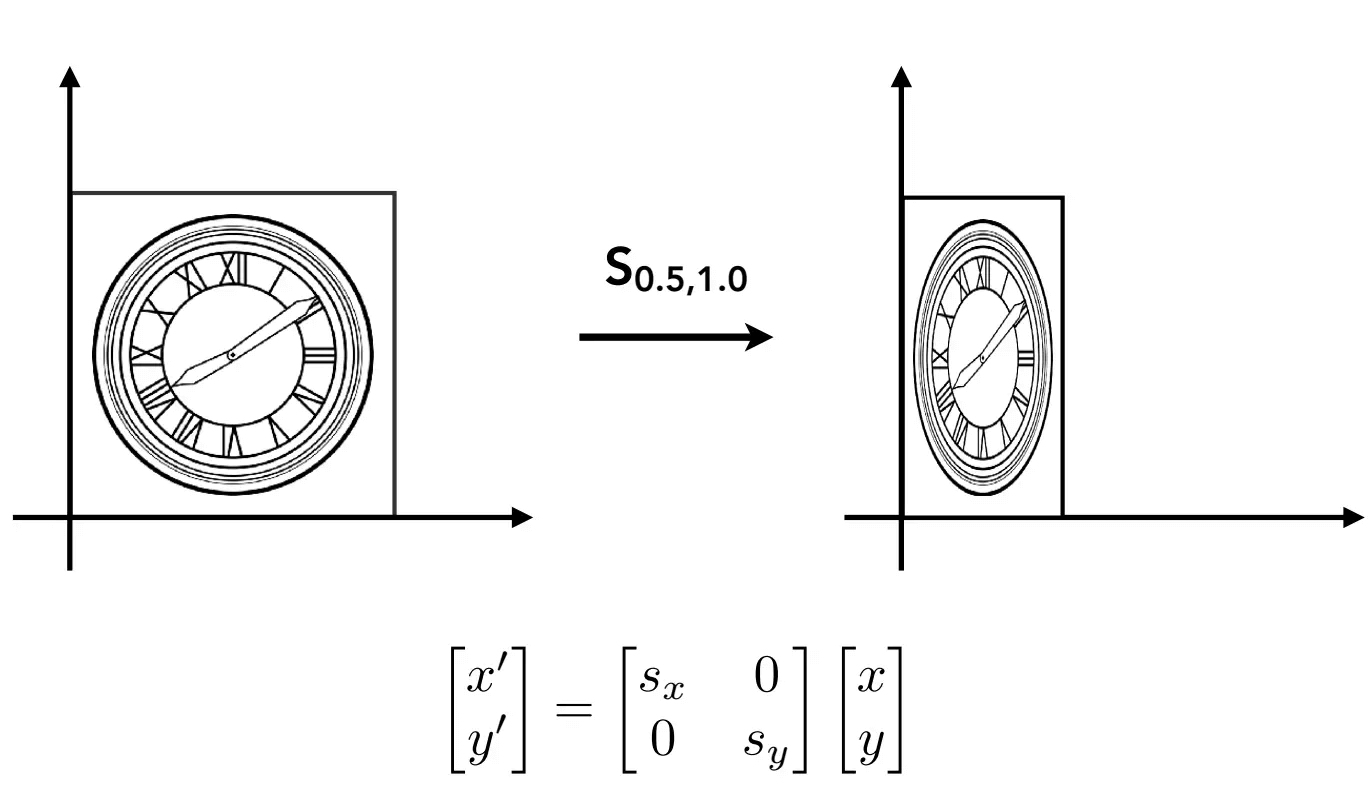
缩放(Scale)

二维

首先是沿主轴方向的缩放：

然后是沿任意方向的缩放，该矩阵将在由单位向量指定的任意方向上按照的因子缩放：

如果需要引入齐次坐标，简单升维即可：

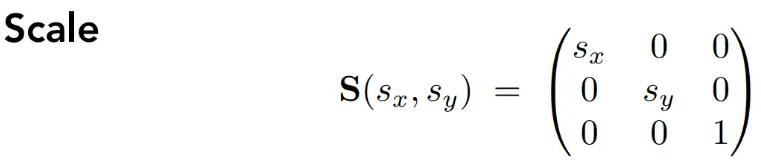
三维

首先是沿主轴方向的缩放，引入齐次坐标：

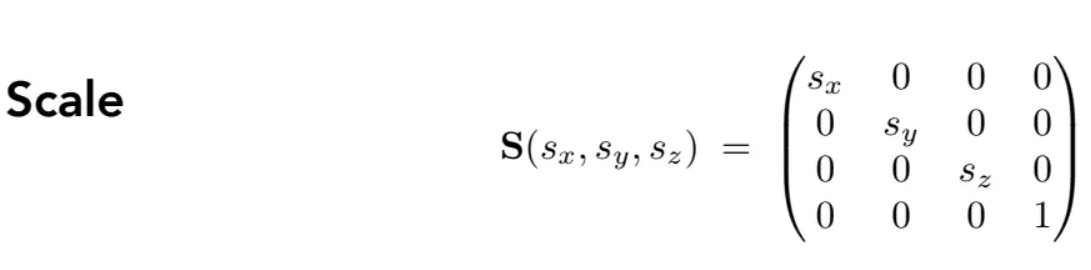
然后是沿任意方向的缩放：

反射(Reflection)

二维

反射，也被称为镜像(Mirroring)，是一种围绕直线(二维)或平面(三维)中”翻转“对象的变换。

在二维中，可以通过应用-1的比例因子来完成反射。设是二维单位矢量，围绕穿过原点并垂直于的反射矩阵如下： 例如如果向按+y方向反射（即按+x方向缩放-1），它的：

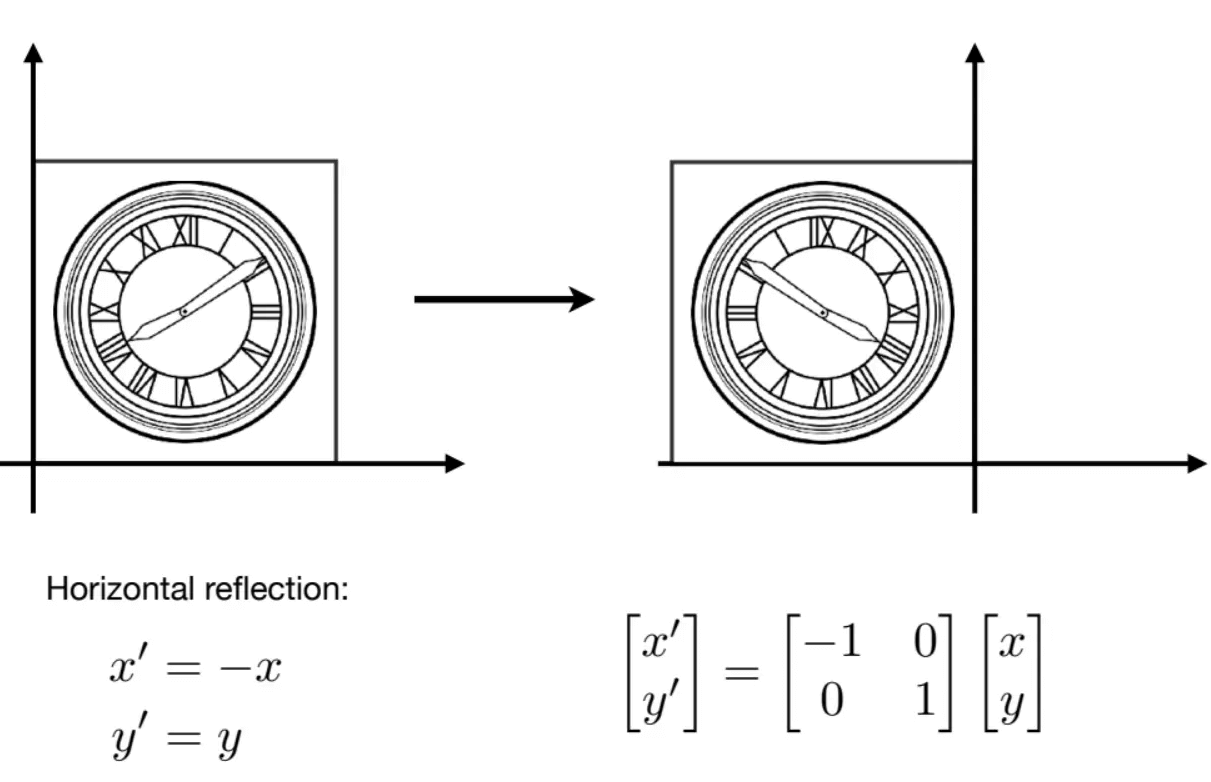
三维

同理，三维中，

错切(Shear)

二维

错切是一种”倾斜“坐标空间的变形，它将不均匀地拉伸坐标空间，不保留角度，但保留了面积/体积。其基本思路是将一个坐标的倍数添加到另一个坐标上。

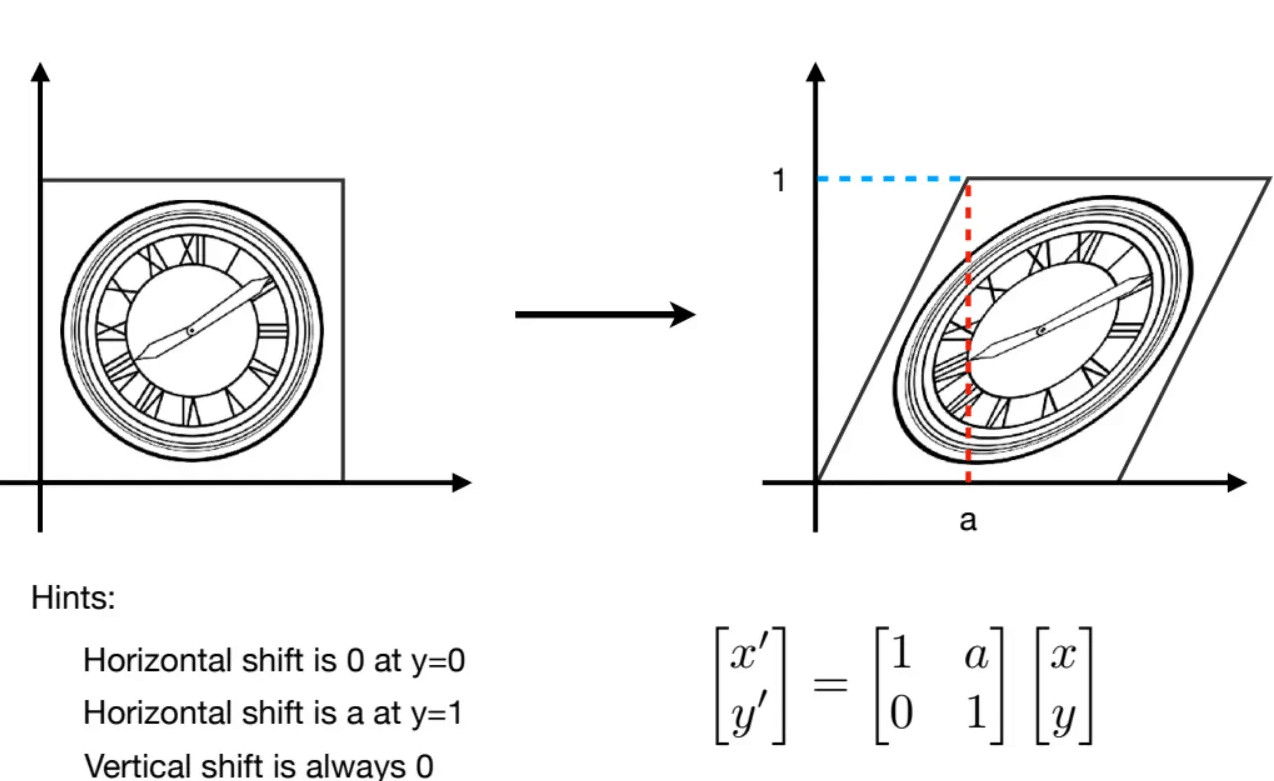
y方向上的同理。

三维

表示x坐标和y坐标按照另一个坐标z移动，即(x’ = x + sz, y’ = y + tz)：

旋转(Rotate)

二维

在二维中，只能进行绕某点旋转的变换。以绕原点，逆时针旋转为默认，矩阵如下：

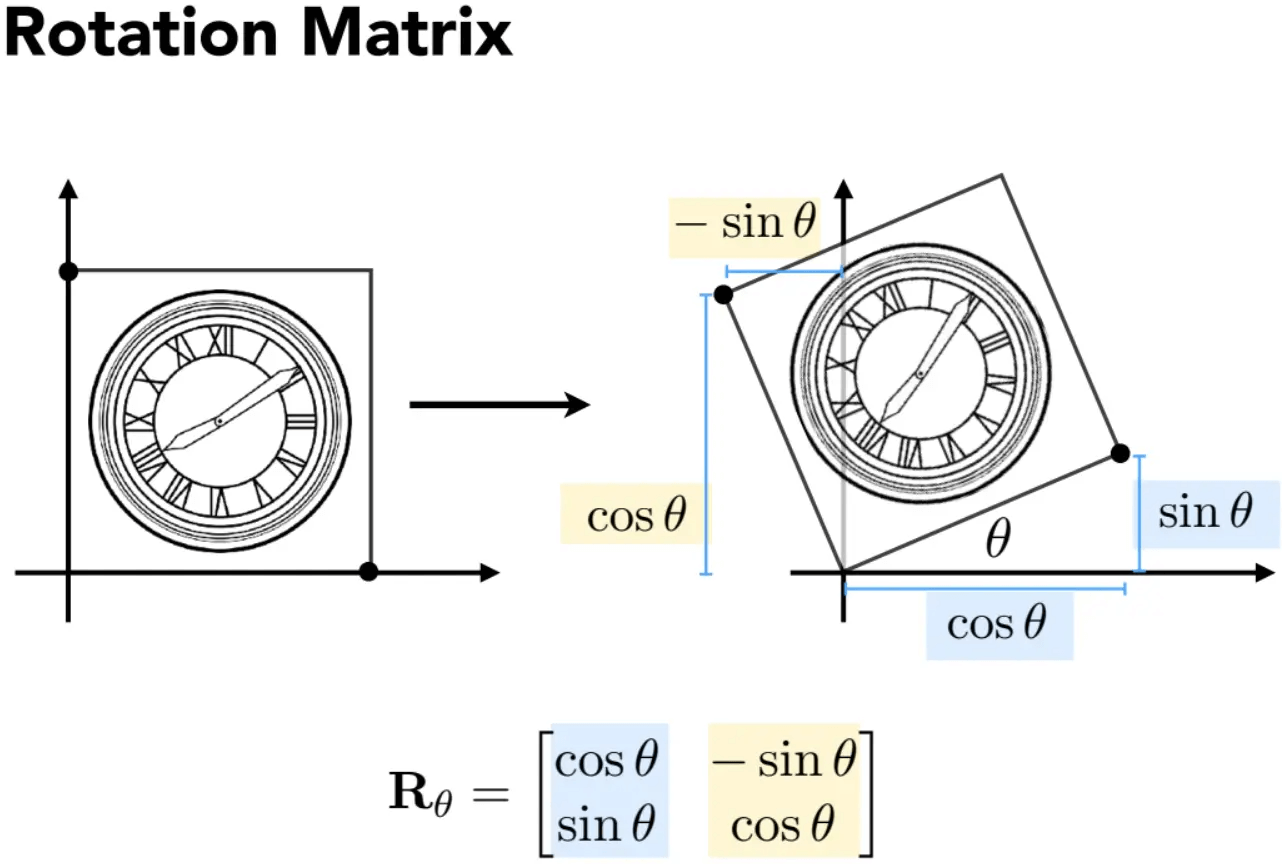
引入齐次坐标系：

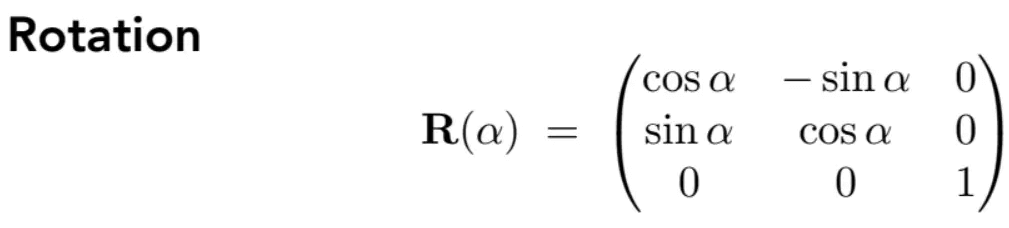
三维

矩阵

考虑如何分别绕三个坐标轴旋转，首先是绕x轴旋转：

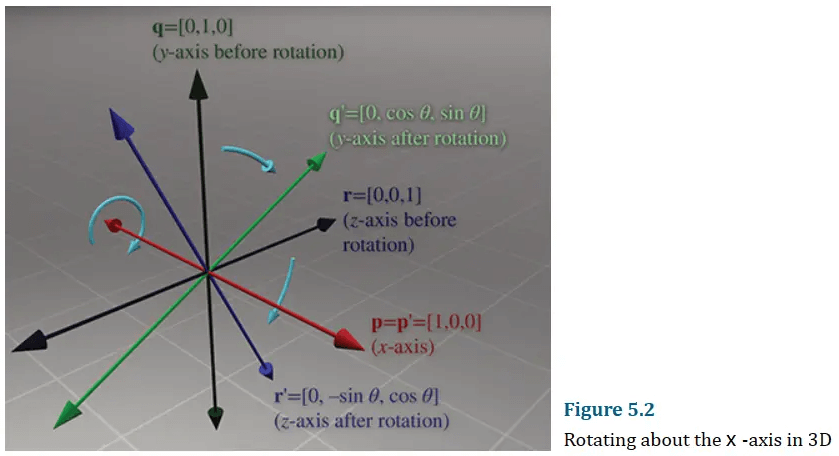
前面的文章说过，矩阵其实是向量的数组，因此我们可以用三个轴的方向向量来表示一个旋转矩阵。按照上图描述，基本旋转矩阵为： 用齐次坐标描述：

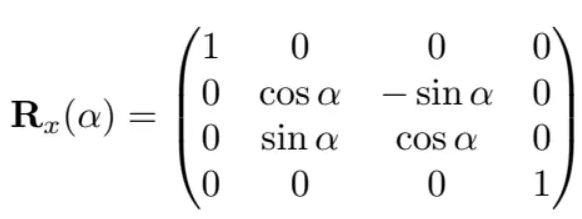
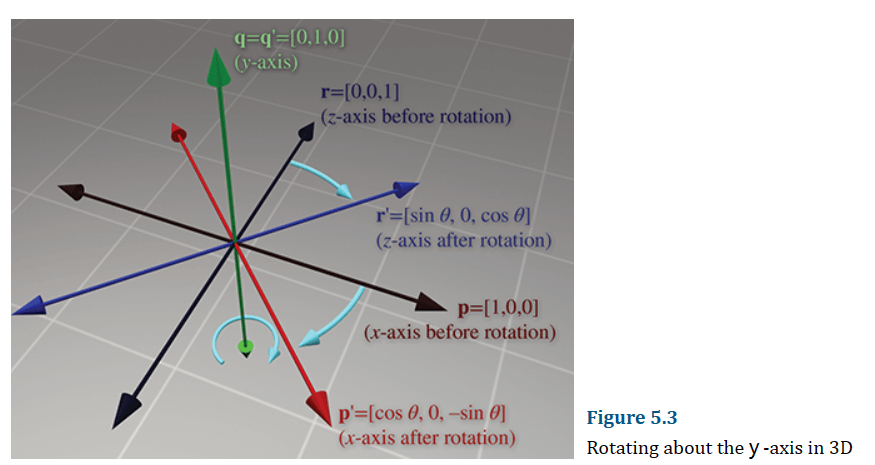
类似的，绕y轴旋转为：

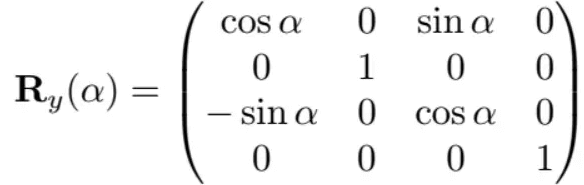
绕z轴旋转为：

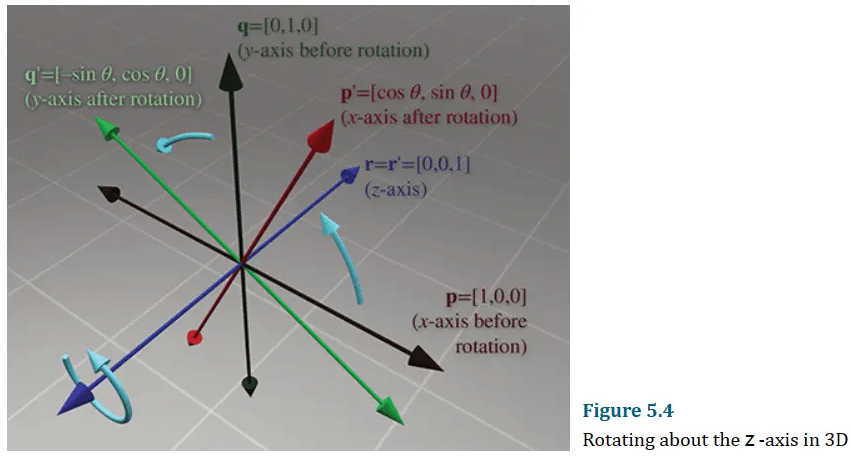
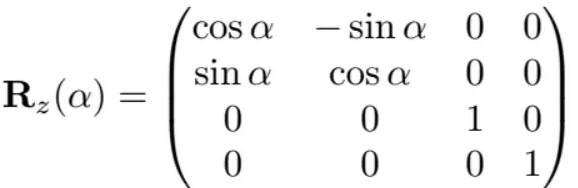
如果想要绕任意方向进行旋转，可以使用罗德里格斯旋转公式：

其中，n为旋转轴，用向量表示；为旋转角度。默认旋转轴是过原点的，如果不过就先平移到原点旋转，再平移回去。

欧拉角

三维旋转也能通过使用欧拉角/四元数来表示，这里先看欧拉角。

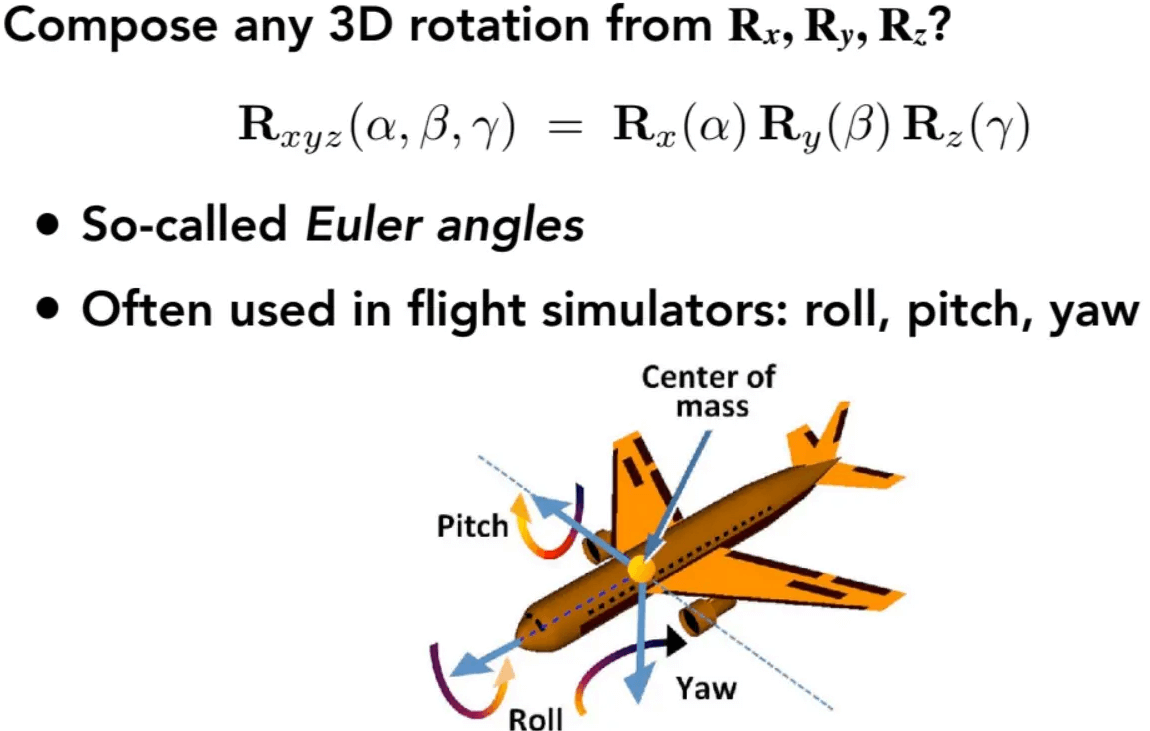
如上图所示，只需将3个绕轴旋转的矩阵结合起来就行了，这三个角在欧拉角中被称为偏航角（Yaw），翻滚角（Roll），俯仰角（Pitch）。

通常情况下，只会选择一个固定的顺序进行旋转，而这会导致万向锁（Gimbal Lock）发生。例如以ZYX顺序进行旋转，首先绕z旋转，然后绕y旋转90°，最后绕x旋转，也就是 可以发现此时旋转只由​决定，而不是三个旋转角，丢失了一个旋转自由度。

万向锁没有简单的解决方案，如果在使用欧拉角的过程中发生了万向锁，那么它们之间的插值可能会变得很怪异或摇摆不定，也就是产生“抖动”。

四元数

有关四元数的基础知识在这里。

定义相关元素如下：

• 表示3D中的一个点
• ，其中是要旋转的角度，是单位矢量旋转轴。这是通过轴-角系统的视角从而定义成这样的。

那么，绕旋转°后的可由以下乘法运算得出： 当然，旋转是可以叠加的，例如将先旋转，再旋转，那么就相当于直接将旋转：

仿射变换(Affine)

线性变换+平移变换。

平移变换(Translation)

二维

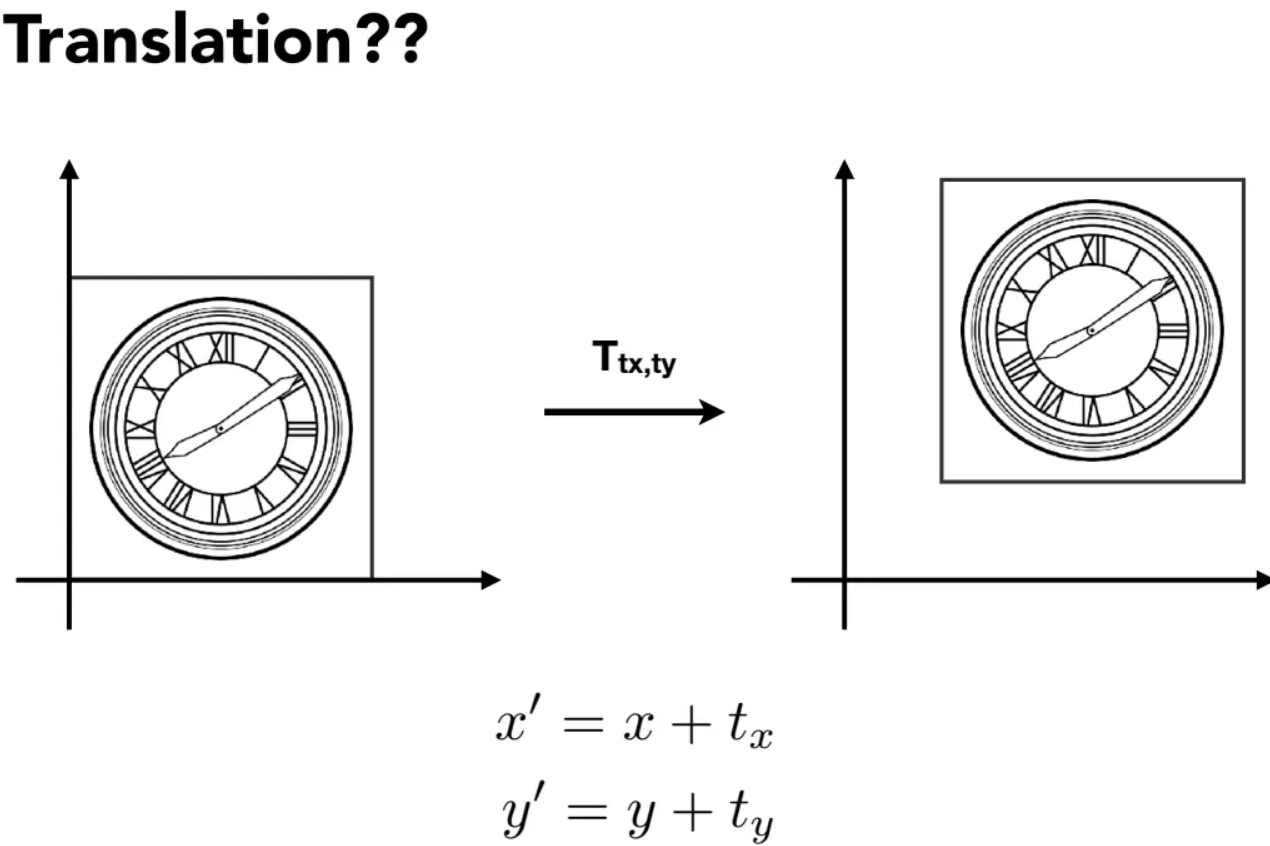
矩阵形式如下：

显然，这种变换写不成线性变换的形式，因为它后边还有加法。我们不想让平移变换成为特例，于是引入齐次坐标，这样，平移就能写成”线性变换“的形式： 这样，就能方便进行组合变换运算了。

三维

引入齐次坐标系：

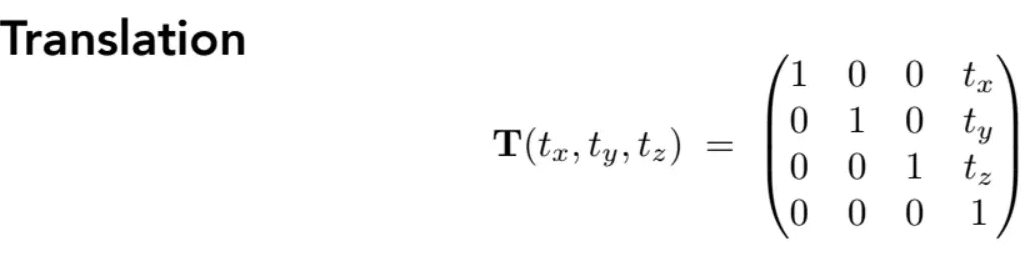
可逆变换(Invertible)

除了投影之外的所有原始变换都是可逆的。

组合变换

顾名思义，就是将上边一堆原始变换组合起来。

例如：

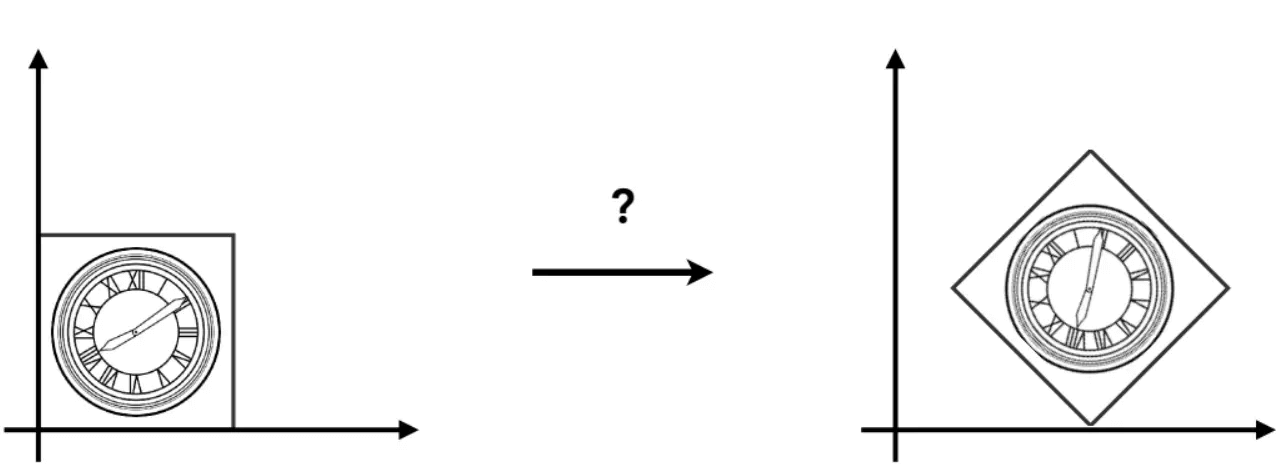
可以先绕原点旋转45°，然后平移过去 (注意变换的次序是重要的，颠倒过来再组合可能不是同一种变换了)：

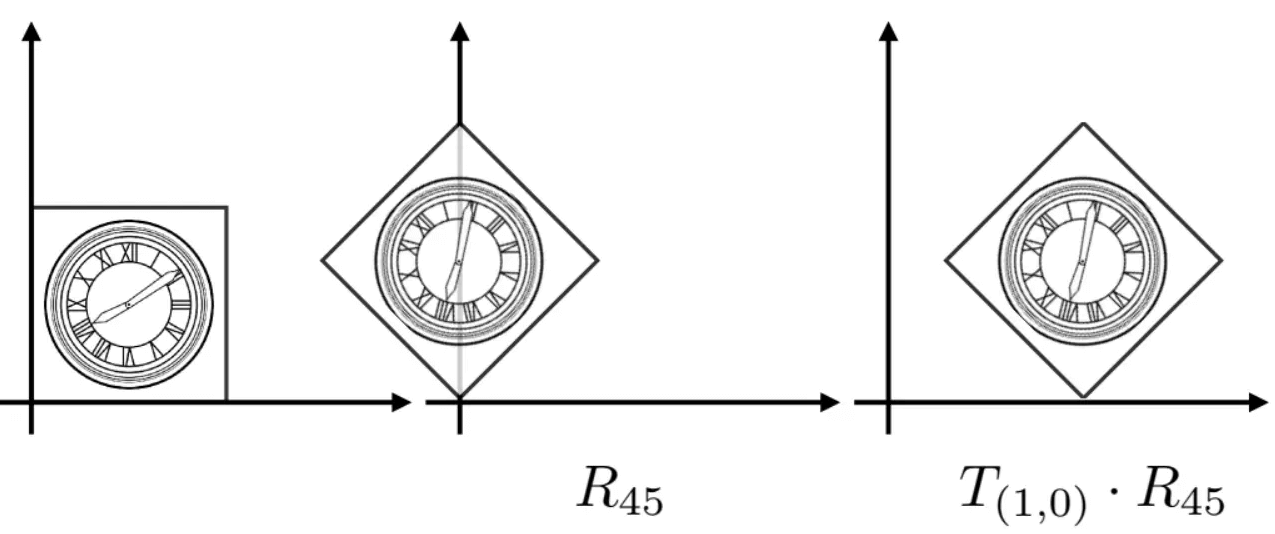
并且注意到，用列向量描述的前提下，矩阵是从右往左乘的：

为了计算简便，可以提前把这些变换矩阵给乘到一起。

参考资料

• GAMES101-现代计算机图形学入门
• 3D数学基础 图形和游戏开发(第2版)
• 万向锁.pdf
• 四元数.pdf
• Release Fall 2023 Lab Docs · XJTU-Graphics/Dandelion-docs (github.com)