矩阵(Matrix)

向量是标量的数组，而矩阵是向量的数组。

单位矩阵(Identity Matrix)

维度为n的单位矩阵，表示为，是矩阵，其对角线上的值为1，其他元素均为0。三维的单位矩阵如下：

矩阵转置(Transpose)

给定矩阵，其转置表示为，是矩阵，其中，列由的行构成。

例如： 一些结论：

矩阵乘法

矩阵与标量相乘

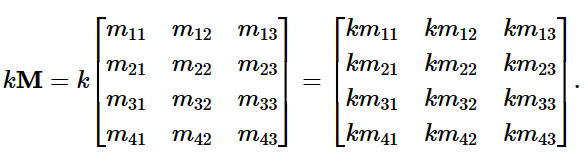
两个矩阵相乘

两个可以相乘的矩阵，必须保证中的列数和中的行数相同，否则结果将是未定义的：

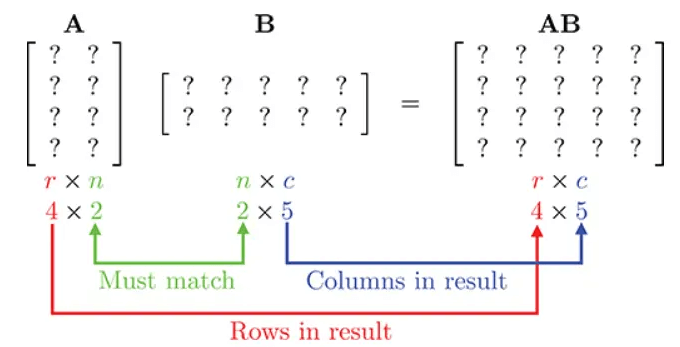
设，则中的每一个元素等于的行i与的列j的向量点积：

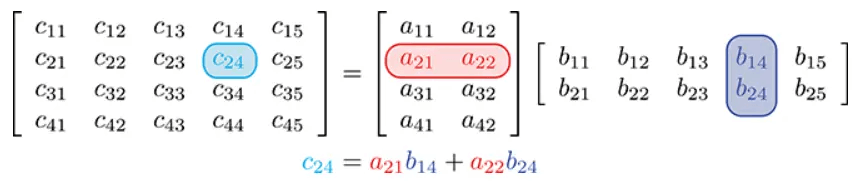
矩阵行列式(Determinant)

方形矩阵的行列式表示为，也可以表示为。

2x2和3x3行列式

例如，一个2x2行列式如下： 一个3x3行列式如下： 如果将3x3行列式看成3个行向量，那么该行列式就是3个行向量的三重积/混合积：

子矩阵行列式(Minor)和余子式(Cofactor)

假设是具有r行和c列的矩阵，删除它的i行和j列，得到一个r-1行和c-1列的新矩阵。如果子矩阵是行列式，可记为，被称为的子矩阵行列式。例如：

而余子式则是在子矩阵行列式的基础上带上了符号：

n x n行列式

已知2x2和3x3行列式是怎么计算的，那么就能根据余子式递归地求解nxn行列式。首先，从矩阵中任选一行/列。然后，对于行/列中的每个元素，将此元素乘以相应的余子式，然后求和即可得出矩阵的行列式。

例如，任意选择行i，行列式可以这样计算： 以3x3矩阵为例：

一些特性

• 任何维度的单位矩阵的行列式为1
• 如果矩阵某行/列都是0，则该矩阵行列式为0
• 交换任意行/列，会让行列式变负
• 将b行/列全部元素的k倍添加到a行/列，行列式值不会改变

逆矩阵(Inverse)

逆矩阵符合下式： 注意，并非所有矩阵都有逆矩阵。

如果某矩阵具有逆矩阵，那么它是 可逆的(Invertible) 或 非奇异的(Nonsingular)；相反，没有逆矩阵的矩阵是不可逆或奇异的。

奇异矩阵的行列式为0。

伴随矩阵求逆

对于较大规模的矩阵求逆，可以通过高斯消元等方法实现；而对于2x2~4x4较小的矩阵，利用伴随矩阵求逆是比较简便的方法。其他方法详见：求逆矩阵的一些方法 - 知乎 (zhihu.com)

矩阵的经典伴随矩阵，表示为，被定义为的余子式的矩阵的转置。

例如有个3x3矩阵，它的伴随矩阵如下： 可以通过伴随矩阵和行列式求得逆矩阵：

一些特性

正交矩阵(Orthogonal Matrix)

定义

当且仅当矩阵及其转置的乘积是单位矩阵时，方形矩阵是正交的： 根据逆矩阵的定义，发现如下性质： 该性质常用于快速求正交矩阵的逆。

如何判断

要使矩阵正交，必须满足以下条件：

• 矩阵的每一行必须是单位矢量
• 矩阵的行必须相互垂直

可以对矩阵的列进行类似描述，因为如果矩阵正交，转置矩阵也正交。

正交化(Orthogonalize)

我们希望通过此操作得到一个矩阵，该矩阵具有相互垂直的单位矢量轴，并且尽可能地接近原矩阵。

（待补充，无偏差的递增正交化算法）

参考资料

• GAMES101-现代计算机图形学入门
• 3D数学基础 图形和游戏开发(第2版)