为什么要多个坐标空间

大多数开发人员发现，在不同情况下使用不同的坐标空间会更方便，因为不同坐标空间的某些信息是有意义的或仅在特定上下文环境中使用。

一些有用的坐标空间

世界空间(World Coordinate System)

世界坐标系是一个特殊的坐标系，它为所有其他要指定的坐标系建立了一个“全局”参考系。也就是说，可以用世界坐标空间来表达其他坐标空间的位置，但不能用任何更大的外部坐标空间来表示世界坐标空间。

世界坐标空间也被称为全局（Global）坐标空间或通用（Universal）坐标空间。

对象空间(Object Space)

对象空间是与特定对象关联的坐标空间，每个对象都有自己独立的对象空间。当一个对象移动或改变方向时，与该对象关联的对象坐标空间也会移动或改变方向。

假设给一个世界的不同对象发送移动指令“向前走”，我们不清楚这些对象以那种绝对方式移动，只会按照他们所认为的“前方”移动（东南西北都有可能），对象坐标空间便发挥大作用；如果给他们发送绝对移动指令“向北走”，这时世界坐标空间便发挥作用了。

在图形学中，对象空间也被称为模型(Model)空间，因为模型顶点的坐标以模型空间表示。在物理环境中，对象空间也被称为体(Body)空间，常见使用场景可能是“相对于体轴”之类的。

相机空间(Camera Space)

对象空间的一个特别重要的示例就是相机空间，它是和用于渲染的视点相关联的对象空间。

使用左手系的相机空间如下图：

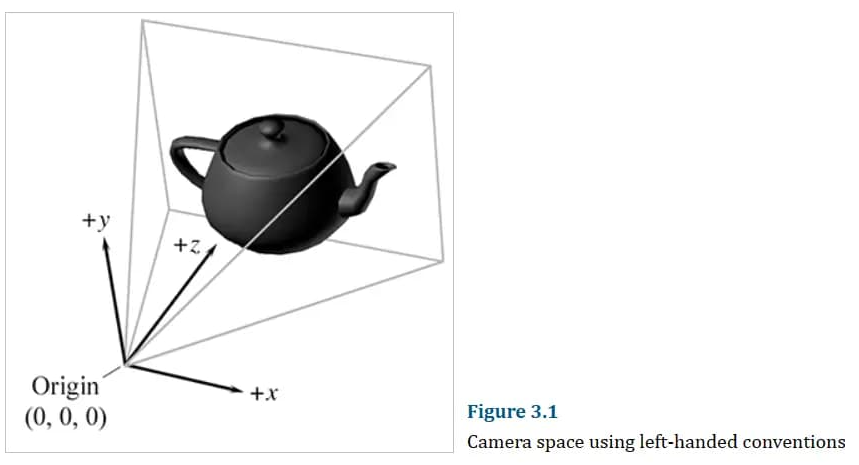
特别要说明的是，OpenGL传统上是右手系，Z轴正方向和左手系的是相反的。

直立空间(Upright Space)

在某种意义上，对象的直立空间是世界空间与其对象空间之间的“中间过渡”，因为直立空间的轴线与世界空间的平行，直立空间的原点与对象空间的重合。以二维的为例：

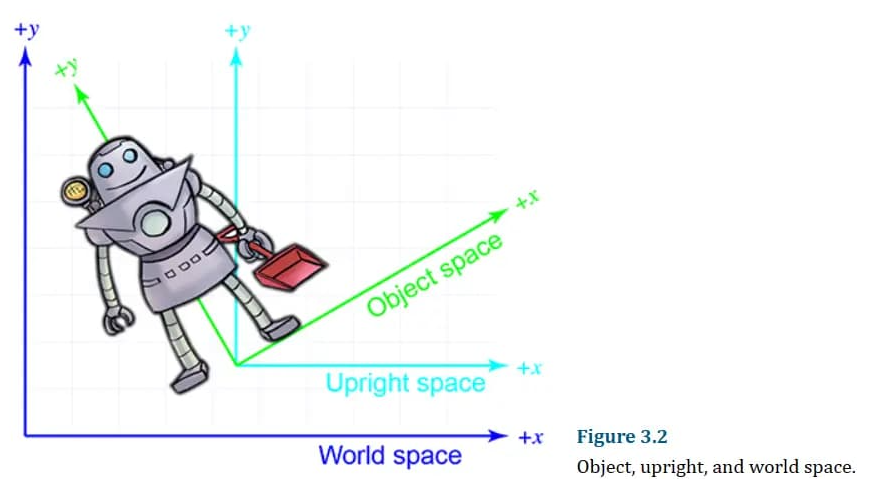
在对象空间和直立空间之间转换点只需要旋转；在世界空间和直立空间之间转换点只需要平移。仍以二维的为例：

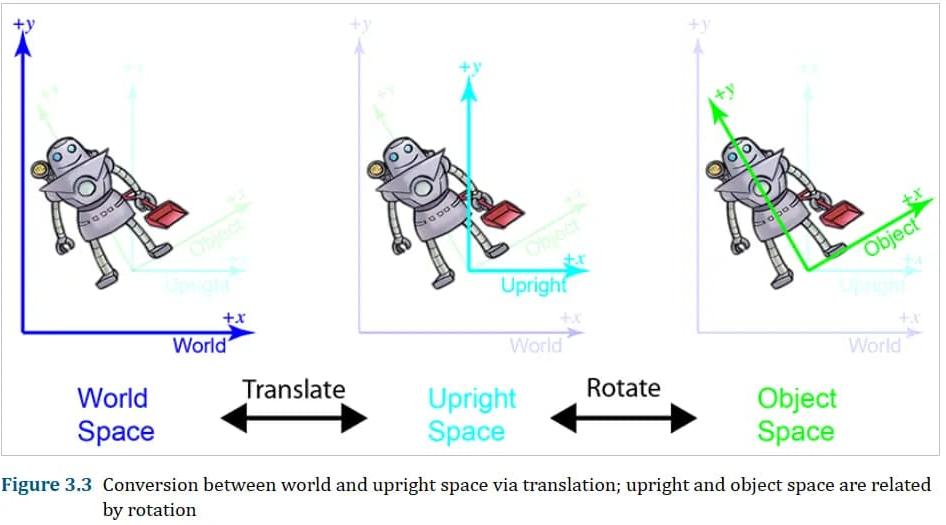
坐标空间转换

现在我们可以在以上任意一个坐标空间中表达一个点了，但我们还需要在一些其他坐标空间中表达这个点，这就是 坐标空间转换(Coordinate Space Transformation)。我们需要将某坐标从世界空间转换为对象空间，或从对象空间转换为世界空间。

例子详见书80页。

如何计算来自对象空间坐标的世界空间坐标：想象将模型从原点移动到它在世界中的位置。

如何计算来自世界空间坐标的相机空间坐标：移动整个世界来将相机放在原点。

双重视角

主动变换范式：用坐标空间固定我们的视角，向量和对象随着它们坐标的变化而移动。见下例左列。

被动变换范式：将视角相对于被变换的对象保持固定，使其看起来好像是正在变换用于测量坐标的坐标空间。见下例右列。

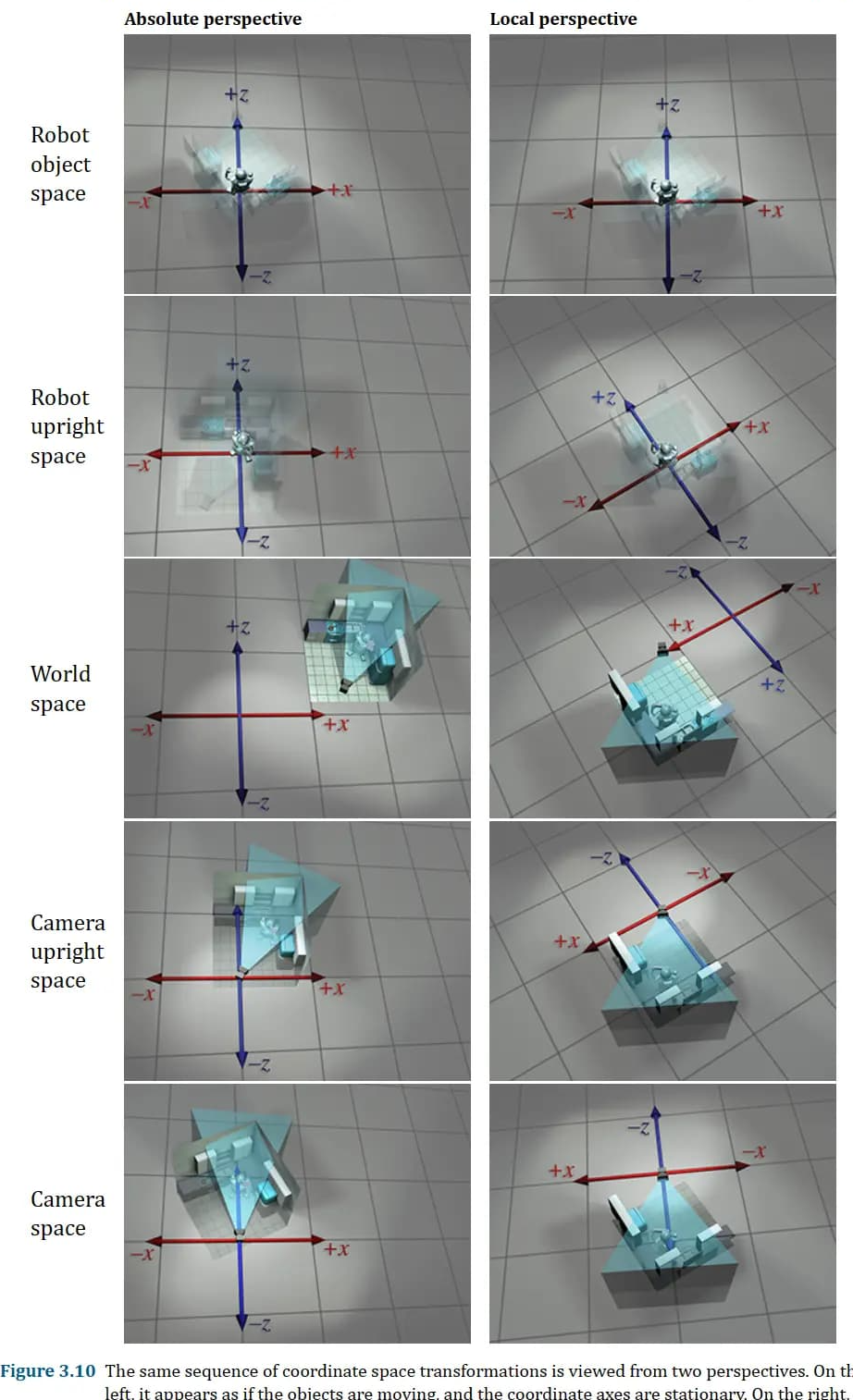
指定坐标空间

现在应该大致清楚不同坐标空间是怎么转换的了，接下来应该步入细节问题：如何指定对象在某一坐标空间的位置？只需要描述它原点或坐标轴在某坐标空间的位置即可。

以上边直立空间的图Figure 3.2为例，机器人对象空间/直立空间原点的世界空间坐标为(4.5，1.5)。接下来使用单位向量在世界空间中描述对象空间+x，+y两个轴的方向（三角学计算，夹角为30°），算得分别为和。

基向量(Basis Vector)

二维例子：

还是以图Figure 3.2为例，先从机器人对象空间中，找到它右肩的大灯坐标为(-1, 5)，也就是相对于原点，向右移动1，向上移动5。接下来，我们通过机器人对象空间原点在世界空间的坐标，间接找到右肩大灯在世界空间的坐标：

1. 确定机器人对象空间原点在世界空间的坐标：(4.5, 1.5)。

2. 向右移动1，知道机器人右边(对象空间-x)的单位向量为；向上移动5，知道机器人上边(对象空间+y)的单位向量为。就能计算了：

这样我们就知道它右肩大灯的世界空间坐标了。继续抽象，设是某对象上的任意点，已知其对象空间(也被称为体空间)坐标为、对象空间原点在世界空间坐标为、对象空间+x，+y方向在世界空间上的单位向量，，则该点在世界空间的坐标为：

定义

根据上面的例子，可以容易的 将三维向量表示为基向量的线性组合： ，，是三维空间的基向量，向量可以具有任何可能的大小和方向，并由坐标(x, y, z)唯一确定（除非选择的基向量很不好）。当我们说正在使用标准基时，只涉及到单一的坐标空间；当我们说正在考虑任何替代基时，则隐式地引入了“用于测量基向量的坐标空间”。

基向量的跨度(Span)

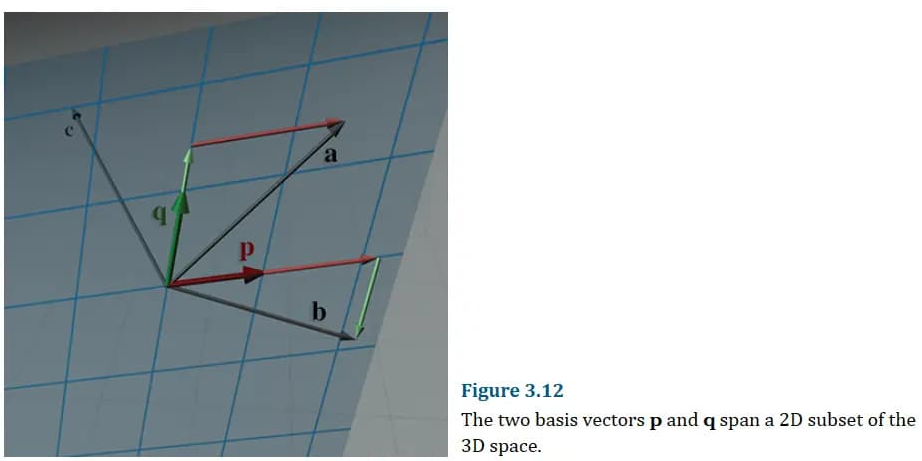
可以表示为基向量的线性组合的向量集被称为基向量的跨度。如图，两个基向量，的线性组合的向量集填充了这个平面，对于此平面中的任意向量，坐标(x, y)的决定具有唯一性，且跨度为这个平面（二维情况下）。

而到了三维中，他们的跨度就是三维空间内的某个任意平面：

基的秩(Rank)

用于描述基所跨越的空间中的维度数就是基的秩。在上例中，有两个跨越二维空间的基向量，这被成为满秩(Full Rank)；如果有两个基向量，但跨度只有一维空间，这就不是满秩了，同时，这两个基向量也是线性相关的，选择这两个线性相关的基向量是“糟糕的”。

正交基(Orthogonal Basis)

一组相互垂直的基向量称为正交基。当基向量正交时，坐标是解耦的。矢量的任何给定坐标可以仅有和相应的基矢量确定。

标准正交基(Orthonormal Basis)

是正交基，且每个基矢量都具有单位长度。在这种特殊情况下，求坐标就变得很简单了。假设知道体轴的世界坐标，且体坐标系的、、构成标准正交基，那么体坐标：

参考资料

• 3D数学基础 图形和游戏开发(第2版)