向量的定义

数学定义

向量就是一串数字数组，我们通常用列向量的方式来表示它：

几何定义

向量是具有 大小 和 方向 的有向线段。

零向量

对于任何给定的向量维度，都有一个特殊的向量，被称为零向量(Zero Vector)： 零向量是特殊的，因为它是唯一的一个大小为零的向量，所有其他向量均具有正大小。此外，零向量也是唯一没有方向的向量。

向量的运算

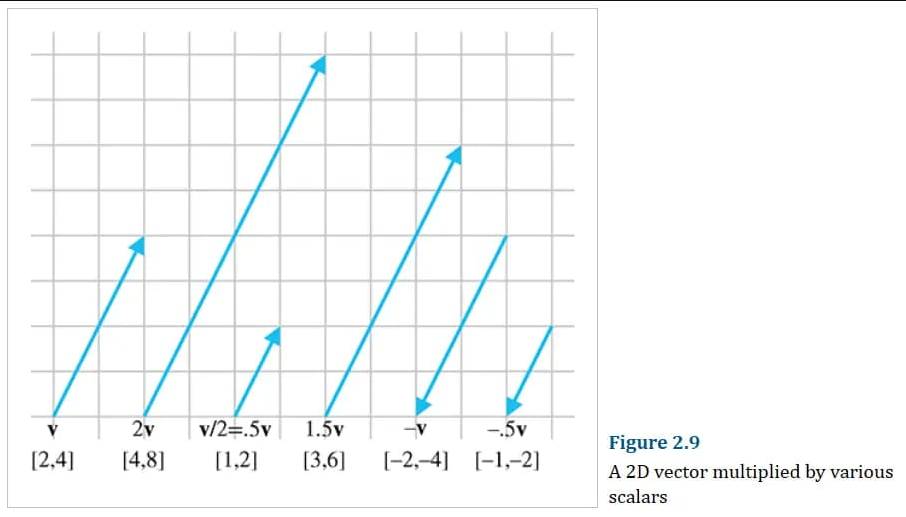
标量和向量的乘除法

只需用标量乘/除向量的每个分量即可： 如果还理解不了，可以看看几何解释。在几何上，将向量乘/除标量k，具有将长度缩放倍的效果：

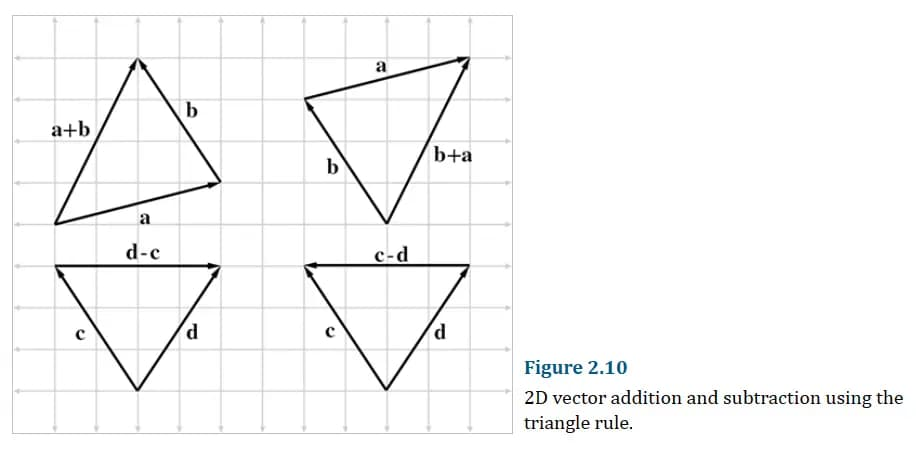
向量的加减法

要使两个向量相加/减，只需分别相加/减他们对应的分量即可： 对于几何解释，这里有三角形法则：

向量的大小

向量的大小是其分量的平方和的平方根，以三维向量为例： 也被称为向量的 范数(Norm)。

对于几何解释，可以用勾股定理来说明（以二维为例，高维度可以推广）：

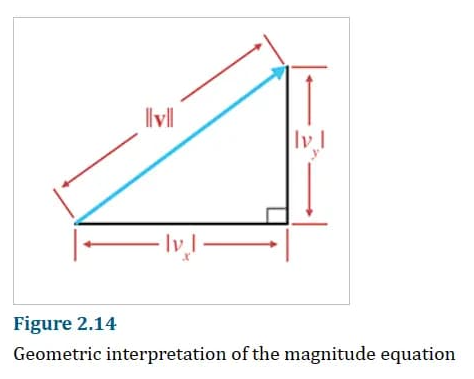
如图，由勾股定理，有： 然后省略右边的绝对值符号，开根号就能得到：

单位向量(Normalized Vector)

有时候，我们只是想用到向量的方向性，而不关注其大小，这时候就能用单位向量(Unit Vector)了。单位向量是大小为1的向量，也被称为标准化向量(Normalized Vector)。

向量标准化的公式如下： 需要注意的是，零向量是无法被标准化的。从数学角度，处于零是不对的；在几何角度，标准化零向量会找不到它的方向。

两点间距离公式

两点间距离公式可由向量减法和向量大小推导出来，三维的公式如下：

向量点积(Dot Product)

向量点积，也称为内积(Inner Product)，在游戏编程中无处不在，其也与矩阵乘法、信号卷积、傅里叶变换等运算有着重要联系。点积的公式如下（以二维为例）：

向量点积是支持交换律，结合律和分配率的。

向量点积主要有以下用途：

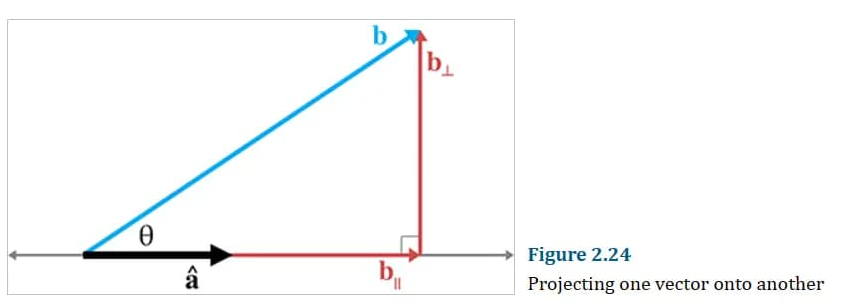
求投影

可以求一个向量到另一个向量的投影：

在上的投影大小为： 然后乘上就好了。

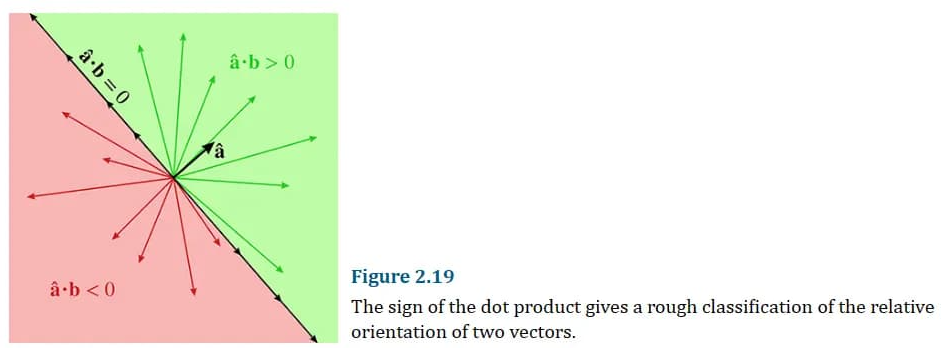
判断相对方向

向量点积结果是个标量，其符号具有判断两向量相对方向的功能：

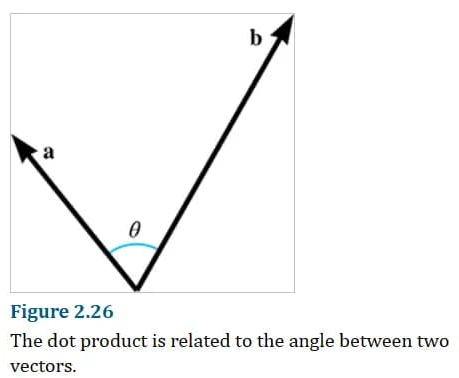
找到两个向量的夹角

由点积公式，可以算出两向量夹角为：

计算向量的大小

向量的大小也能通过点积进行计算：

沿某向量进行正交分解

给定以下两个向量： 将分解成与垂直和平行的分量。

先求平行的，也就是在上的投影，已知它的长度为： 然后再乘上即可（因为上边得到的是标量，这里要变成向量）： 然后垂直的就简单了：

向量叉积(Cross Product)

向量叉积只能在三维中引用，其产生三维矢量并且不是可变换的。

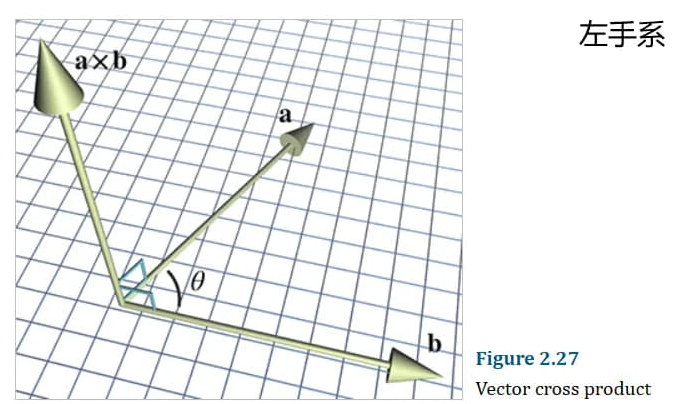
叉积的公式如下： 叉积的大小公式如下： 可以得出，当两非零向量平行时，他们叉积的结果为零向量；自己和自己叉积的结果也是零向量。

除此之外，叉积的常见性质如下：

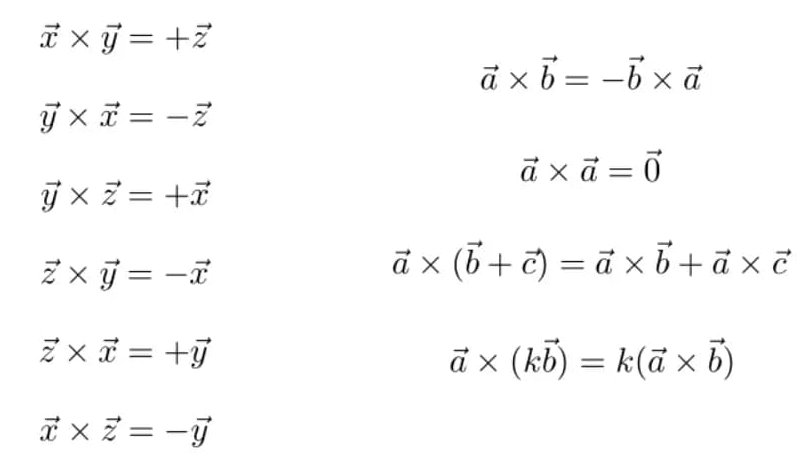
向量叉积主要有以下用途：

判断从向量a到b是什么时针方向转动

可以把的尾部放到的头部，然后通过左右手（看坐标系）的大拇指规则来判断：

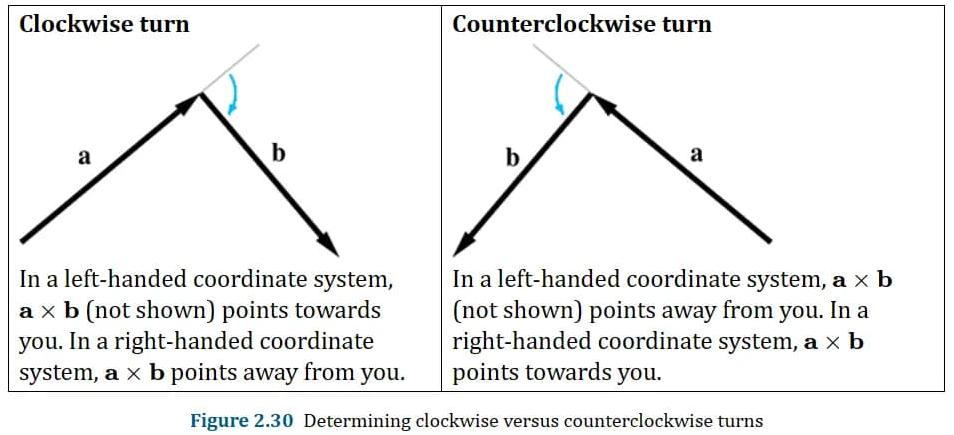
也能用来判断两向量的左/右侧关系。

判断点在向量组成的图形内外

绕同一个方向判断这个向量与其他所有向量的左右测关系，如果都一致则在内部。

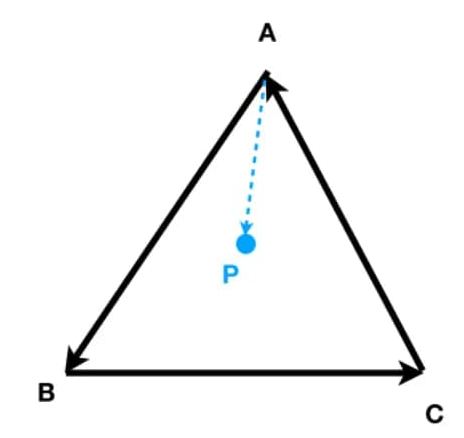
参考资料

• GAMES101-现代计算机图形学入门
• 3D Math Primer for Graphics and Game Development