开始学习大名鼎鼎的光追三部曲系列中的：Ray Tracing: The Rest of Your Life！希望我能坚持下去吧。

简单蒙特卡洛程序

接下来从一个最简单的蒙特卡洛程序开始。有两种随机算法：蒙特卡洛算法和拉斯维加斯算法。

一个随机算法会在计算中产生一些随机量。对于拉斯维加斯算法，它总是可能给出正确的结果（有时候是错的）。但对于光线追踪这种极其复杂的问题，我们可能不会把问题答案的合理性放到最优先。拉斯维加斯算法最终会得到正解，但无法保证花费的时间有多长。一个拉斯维加斯算法的经典例子就是快速排序算法，它总是以一个排列好的数组结束，但需要随机时间完成。另一个例子就是我们之前写的在单位球中随机采样：

inline Vec3 random_in_unit_sphere() {
    while (true) {
        auto p = Vec3::random(-1,1);
        if (p.length_squared() < 1)
            return p;
    }
}

这个代码最终会返回单位球内的随机向量，但无法保证花费了多长时间。

蒙特卡洛算法将会给出一个统计估计的答案，且这种估计会随着程序运行时间越来越精准。这说明当我们认为答案差不多对的时候，就能退出程序了。答案可能会有点噪音，不过够用了。

估计Pi

蒙特卡洛算法的范例就是估计。有许多种估计的方法，这里使用 布封投针问题 来估计它。

假设有一个包在正方形里的圆：

现在假设你从正方形里随机选一些点，在圆里的点 / 总点数 应该和圆的面积成正比如下： 那么就能估计出，代码如下：

std::cout << std::fixed << std::setprecision(12);

int inside_circle = 0;
int N = 100000;
for (int i = 0; i < N; ++i)
{
    auto x = random_double(-1, 1);
    auto y = random_double(-1, 1);
    if (x * x + y * y < 1)
        inside_circle++;
}

std::cout << "Pi: " << (4.0 * inside_circle) / N << '\n';

// 结果:
Pi: 3.140840000000

展示收敛性

如果让程序一直运行，只是在适当情况下输出估计值：

std::cout << std::fixed << std::setprecision(12);

int inside_circle = 0;
int runs = 0;
while (true)
{
    ++runs;
    auto x = random_double(-1, 1);
    auto y = random_double(-1, 1);
    if (x * x + y * y < 1)
        inside_circle++;

    if (runs % 100000 == 0)
        std::cout << "Estimate of Pi: " << (4.0 * inside_circle) / runs << '\n';
}

分层抖动采样

可以发现上面的结果已经很接近了，但始终在上下浮动。这是一个收益递减规律的例子，每次采样对结果的帮助都不大。这就是蒙特卡洛方法最糟糕的地方。可以通过分层抖动采样的方式减缓这种现象，将采样区域划分为网格，每对网格随机采样一次，而不是纯随机采样。

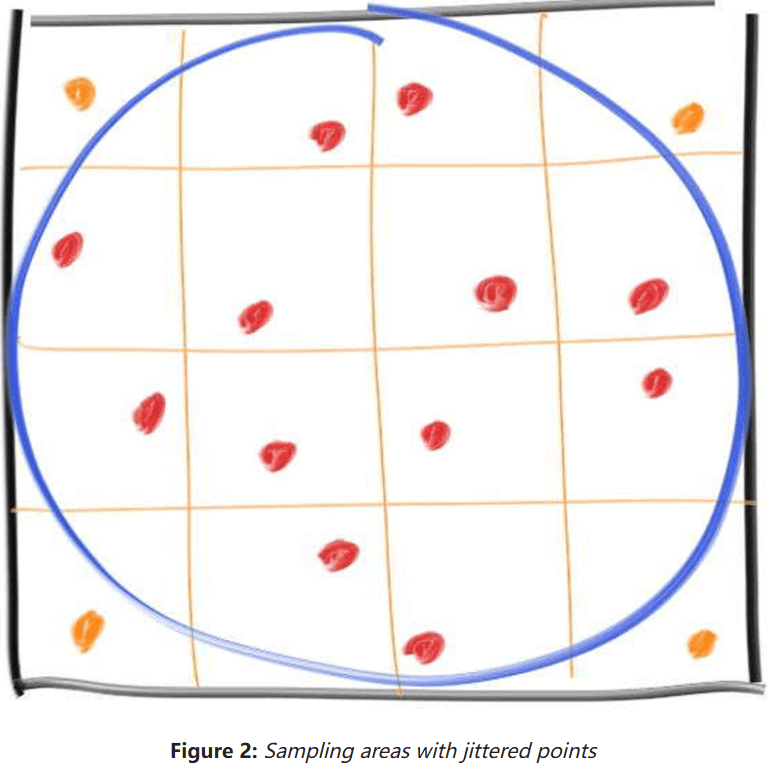
让我们试试分层抖动采样和纯随机采样，采样一百万次：

std::cout << std::fixed << std::setprecision(12);

int inside_circle = 0;
int inside_circle_stratified = 0;
int sqrt_N = 1000;

for (int i = 0; i < sqrt_N; ++i)
{
    for (int j = 0; j < sqrt_N; ++j)
    {
        // 随机采样
        auto x = random_double(-1, 1);
        auto y = random_double(-1, 1);
        if (x * x + y * y < 1)
            inside_circle++;

        // 分层抖动采样
        x = 2 * ((i + random_double()) / sqrt_N) - 1;
        y = 2 * ((j + random_double()) / sqrt_N) - 1;
        if (x * x + y * y < 1)
            inside_circle_stratified++;

    }
}
    
std::cout << "Regular Estimate of Pi: " << (4.0 * inside_circle) / (sqrt_N * sqrt_N) << '\n'
    << "Stratified Estimate of Pi: " << (4.0 * inside_circle_stratified) / (sqrt_N * sqrt_N) << '\n';

输出结果如下：

Regular Estimate of Pi: 3.141168000000
Stratified Estimate of Pi: 3.141404000000

可以发现分层抖动抽样的结果比常规随机抽样的好。但它的优势随着采样维度的增加而减弱，这就是所谓的维数灾难。光线追踪是一个很高维的算法，每次反射都会添加两个维度：和。在这里我们不会对输出的反射角分层抖动抽样，因为太复杂了。

接下来对康奈尔盒场景进行分层抖动采样，首先先跑一遍原来的场景做对比用：

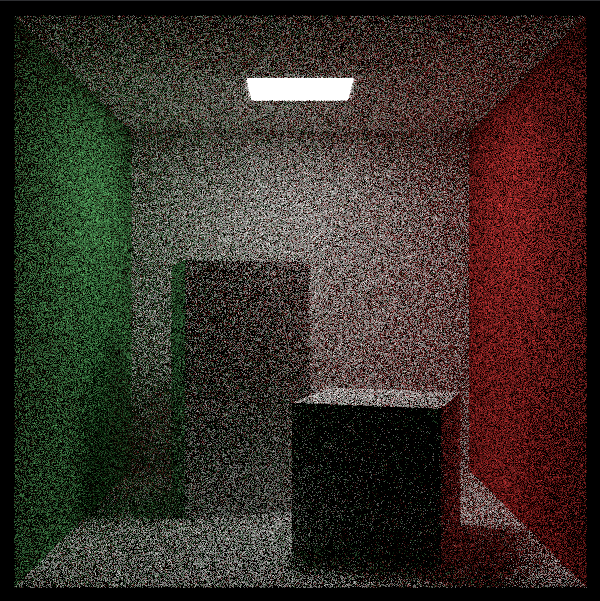
接下来在Camera类中实现分层抖动采样：

参考资料

• Ray Tracing: The Rest of Your Life